Елементи комбінаторики

При розв'язуванні багатьох задач з теорії ймовірностей доводиться підраховувати число різних варіантів. Розділ математики, в якому розглядаються задачі, пов'язані із скінченими множинами та складанням різних комбінацій з елементів цих множин, називається комбінаторикою.

Комбінаторику використовують не тільки у теорії ймовірностей, але й при розв'язуванні задач економіки, теорії обчислювальних машин тощо.

Правило добутку.Якщо компоненту х₁ рядка (х₁, х₂,...,х_k) можна вибрати n₁ способами, компоненту х₂ – n₂ способами, ..., х_k – n_k способами, то існує N = n₁×n₂...n_k можливостей утворення рядка (х₁, х₂,..., х_k).

 

Приклад.В їдальні є чотири перших блюда, п'ять других і три третіх. Скількома способами можна скласти із них обід?

Розв'язання:

Обіду можна поставити у взаємо-однозначну відповідність рядок (х₁, х₂, х₃), де х₁ можна вибрати n₁ = 4 способами, х₂ – n₂ = 5 способами, а х₃ – n₃ = 3 способами. Значить існує N = n₁×n₂×n₃ = 4×5×3 = = 60 можливих способів вибору обіду.

Перестановки. Нехай маємо множину із n елементів. Будемо переставляти їх між собою. Одержуємо кожен раз нові упорядковані множини, що відрізняються одна від одної тільки порядком наслідування елементів. Їх називають перестановками із n елементів і позначають через Р_n. Знаходять перестановки за формулою Р_n = n!, де n! = 1 × 2 × 3 ×... × (n – 1) n. За означенням 0! = 1.

Приклад. Скількома способами можна розсадити в аудиторії 6 студентів?

Розв'язання. Р₆ = 6! = 1 × 2 × 3 × 4 × 5 × 6 = 720.

 

Розміщення.Маємо множину із n елементів, із яких утворюємо підмножини по m елементів (m <= n), такі, що відрізняються одна від одної або самими елементами, або їх порядком. Такі впорядковані підмножини називають розміщенням і позначають А_n^m.

 

Приклад. Із чотирьох елементів А, В, С, D можна утворити такі розміщення по два:

АВ,АС,АD,BC,BD,CD	Всього
BA,CA,DA,CB,DB,DC

 

Можна довести, що А_n^m =n(n – 1)(n – 2) ... [n – (m – 1)], або

 

(1)

 

Комбінації або сполучення (російською – сочетания). Маємо множину із n елементів, із якої утворюємо підмножини по m елементів (m £ n), такі, що відрізняються одна від одної хоча б одним елементом. Такі впорядковані підмножини називають комбінаціями і

Позначають C_n^m.

У наведеному прикладі очевидно, що C₄² = 6.

Взагалі доводиться, що

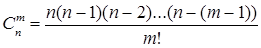(2)

Із (2) з врахуванням (1) можна одержати, що

(3)

 

За останньою формулою легко довести, що

. Так .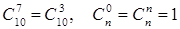

1.4.3. Теорема додавання ймовірностей

Теорема.Ймовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій.

 

Доведення:

Нехай А і В – дві несумісні події і n – загальне число випадків, із яких події А сприяє m₁ випадків, а В – m₂. Тоді за класичною формулою ймовірностей маємо

P(A)=m₁/n, P(B)=m₂/n.

 

Оскільки події А і В несумісні, то m₁ випадків, що сприяють події А, не сприяють події В і m₂ випадків, що сприяють події В, не сприяють події А. Отже, сумі подій А + В сприяють m₁ + m₂ випадки із загального числа випадків n. За класичною формулою теорії ймовірностей

Теорема доведена.

 

Методом повної математичної індукції можна довести, що теорема справедлива для випадку А₁, А₂, ..., А_n несумісних подій, тобто

Р(А₁ + А₂ + ... + А_n) = Р(А₁) + P(А₂) + ... + Р(А_n)

Приклад. У грошево-речовій лотереї на кожні 10000 білетів розігруються 150 речових і 50 грошових виграшів. Чому дорівнює ймовірність виграшу, речового або грошового для власника одного білета.

Розв’язання:

Всього n = 10000 несумісних, рівноможливих і таких, що утворюють повну групу, подій. Подія А – речовий виграш, В – грошовий.

Р(А) = 150/10000 = 0,015; Р(В)=50/10000 = 0,005.

Оскільки А і В – несумісні події (на один квиток можна одержати або речовий, або грошовий виграш), то

Р(А + В)=Р(А) + Р(В) = 0,015 + 0,005 = 0,02 (2 %).

Наслідок 1. Якщо події А₁, А₂, ..., А_n утворюють повну групу несумісних подій, то сума їх ймовірностей дорівнює 1.

Доведення:

Так як події А₁, А₂, ..., А_n утворюють повну групу несумісних по­дій, то поява хоча б однієї з них вірогідна подія і Р(А₁ + А₂ + ... + А_n) = = 1, а так як А₁, А₂, ..., А_n несумісні, то за доведеною теоремою

Отже

Дві несумісні події, що утворюють повну групу, називаються протилежними.

Приклад. Нехай подія А – виріб вищого ґатунку. Протилежною подією 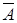є виріб не вищого ґатунку.

 

Наслідок 2.Сума ймовірностей протилежних подій дорівнює одиниці:

(1)

Цей наслідок є наслідком наслідка1. Із (1) випливає, що

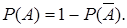(2)

Формула (2) дуже важлива для розв’язування задач.

Приклад. У партії з 10 деталей 7 стандартних. Знайти ймовірність того, що серед навздогад вилучених двох деталей є хоча б одна стандартна.

Розв’язання:

Подія А – серед вилучених деталей є хоча б одна стандартна, 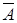– немає стандартних.