Проверка статистических гипотез
Лекция 19.
Статистическая проверка статистических гипотез. Общие принципы проверки гипотез. Понятия статистической гипотезы (простой и сложной), нулевой и конкурирующей гипотезы, ошибок первого и второго рода, уровня значимости, статистического критерия, критической области, области принятия гипотезы. Наблюдаемое значение критерия. Критические точки. Мощность критерия. Критерии для проверки гипотез о вероятности события, о математическом ожидании, о сравнении двух дисперсий.
Определение 19.1. Статистической гипотезой называют гипотезу о виде неизвестного распределения генеральной совокупности или о параметрах известных распределений.
Определение 19.2. Нулевой (основной) называют выдвинутую гипотезу Н0. Конкурирую-щей (альтернативной)называют гипотезу Н1, которая противоречит нулевой.
Пример. Пусть Н0 заключается в том, что математическое ожидание генеральной совокупности а = 3. Тогда возможные варианты Н1: а) а ≠ 3; б) а > 3; в) а < 3.
Определение 19.3. Простой называют гипотезу, содержащую только одно предположение, сложной – гипотезу, состоящую из конечного или бесконечного числа простых гипотез.
Пример. Для показательного распределения гипотеза Н0: λ = 2 – простая, Н0: λ > 2 – сложная, состоящая из бесконечного числа простых ( вида λ = с, где с – любое число, большее 2).
В результате проверки правильности выдвинутой нулевой гипотезы ( такая проверка называется статистической, так как производится с применением методов математичес-кой статистики) возможны ошибки двух видов: ошибка первого рода, состоящая в том, что будет отвергнута правильная нулевая гипотеза, и ошибка второго рода, заключаю-щаяся в том, что будет принята неверная гипотеза.
Замечание. Какая из ошибок является на практике более опасной, зависит от конкретной задачи. Например, если проверяется правильность выбора метода лечения больного, то ошибка первого рода означает отказ от правильной методики, что может замедлить лече-ние, а ошибка второго рода (применение неправильной методики) чревата ухудшением состояния больного и является более опасной.
Определение 19.4. Вероятность ошибки первого рода называется уровнем значимости α.
Основной прием проверки статистических гипотез заключается в том, что по имеющейся выборке вычисляется значение некоторой случайной величины, имеющей известный закон распределения.
Определение 19.5.Статистическим критерием называется случайная величина К с известным законом распределения, служащая для проверки нулевой гипотезы.
Определение 19.6. Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают.
Итак, процесс проверки гипотезы состоит из следующих этапов:
1) выбирается статистический критерий К;
2) вычисляется его наблюдаемое значение Кнабл по имеющейся выборке;
3) поскольку закон распределения К известен, определяется (по известному уровню значимости α) критическое значениеkкр, разделяющее критическую область и область принятия гипотезы (например, если р(К > kкр) = α, то справа от kкр распо-лагается критическая область, а слева – область принятия гипотезы);
4) если вычисленное значение Кнабл попадает в область принятия гипотезы, то нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается.
Различают разные виды критических областей:
- правостороннююкритическую область, определяемую неравенством K > kкр ( kкр > 0);
- левостороннюю критическую область, определяемую неравенством K < kкр ( kкр < 0);
- двустороннюю критическую область, определяемую неравенствами K < k1, K > k2 (k2 > k1).
Определение 19.7. Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что верна конкурирующая гипотеза.
Если обозначить вероятность ошибки второго рода (принятия неправильной нулевой гипотезы) β, то мощность критерия равна 1 – β. Следовательно, чем больше мощность критерия, тем меньше вероятность совершить ошибку второго рода. Поэтому после выбора уровня значимости следует строить критическую область так, чтобы мощность критерия была максимальной.
Критерий для проверки гипотезы о вероятности события.
Пусть проведено п независимых испытаний (п – достаточно большое число), в каждом из которых некоторое событие А появляется с одной и той же, но неизвестной вероятностью р, и найдена относительная частота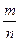 
появлений А в этой серии испытаний. Проверим при заданном уровне значимости α нулевую гипотезу Н0, состоящую в том, что вероятность р равна некоторому значению р0.
Примем в качестве статистического критерия случайную величину
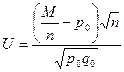, (19.1)
имеющую нормальное распределение с параметрами M(U) = 0, σ(U) = 1 (то есть нормиро-ванную). Здесь q0 = 1 – p0. Вывод о нормальном распределении критерия следует из теоремы Лапласа (при достаточно большом п относительную частоту можно приближенно считать нормально распределенной с математическим ожиданием р и средним квадрати-ческим отклонением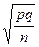 
).
Критическая область строится в зависимости от вида конкурирующей гипотезы.
1) Если Н0: р = р0, а Н1: р ≠ р0, то критическую область нужно построить так, чтобы вероятность попадания критерия в эту область равнялась заданному уровню значимости α. При этом наибольшая мощность критерия достигается тогда, когда критическая область состоит из двух интервалов, вероятность попадания в каждый из которых равна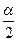 
. Поскольку U симметрична относительно оси Оу, вероятность ее попадания в интервалы (-∞; 0) и (0; +∞) равна 0,5, следовательно, критическая область тоже должна быть симметрична относительно Оу. Поэтому икр определяется по таблице значений функции Лапласа из условия 
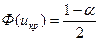, а критическая область имеет вид 
.
Замечание. Предполагается, что используется таблица значений функции Лапласа, заданной в виде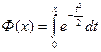 
, где нижний предел интегрирования равен 0, а не -∞. Функция Лапласа, заданная таким образом, является нечетной, а ее значения на 0,5 меньше, чем значения стандартной функции Ф(х) (см. лекцию 6).
Далее нужно вычислить наблюдаемое значение критерия:
. (19.2)
Если |Uнабл| < uкр, то нулевая гипотеза принимается.
Если |Uнабл| > uкр, то нулевая гипотеза отвергается.
2) Если конкурирующая гипотеза Н1: р > p0, то критическая область определяется неравенством U > uкр, то есть является правосторонней, причем р(U > uкр) = α. Тогда 
. Следовательно, икр можно найти по таблице значений функции Лапласа из условия, что 
. Вычислим наблюдаемое значение критерия по формуле (19.2).
Если Uнабл < uкр, то нулевая гипотеза принимается.
Если Uнабл > uкр, то нулевая гипотеза отвергается.
3) Для конкурирующей гипотезы Н1: р < p0 критическая область является левосторонней и задается неравенством U <- uкр, где икр вычисляется так же, как в предыдущем случае.
Если Uнабл > - uкр, то нулевая гипотеза принимается.
Если Uнабл < - uкр, то нулевая гипотеза отвергается.
Пример. Пусть проведено 50 независимых испытаний, и относительная частота появления события А оказалась равной 0,12. Проверим при уровне значимости α = 0,01 нулевую гипотезу Н0: р = 0,1 при конкурирующей гипотезе Н1: р > 0,1. Найдем 
Критическая область является правосторонней, а икр нахо-дим из равенства Ф(икр) =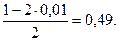 
Из таблицы значений функции Лапласа определяем икр = 2,33. Итак, Uнабл < uкр, и гипотеза о том, что р = 0,1, принимается.
Критерий для проверки гипотезы о математическом ожидании.
Пусть генеральная совокупность Х имеет нормальное распределение, и требуется проверить предположение о том, что ее математическое ожидание равно… 1) Известна дисперсия σ2 генеральной совокупности. Тогда по выборке… Учитывая, что выборочное среднее является несмещенной оценкой М(Х), то есть М() = М(Х), можно записать нулевую…Критерий для проверки гипотезы о сравнении двух дисперсий.
Пусть имеются две нормально распределенные генеральные совокупности Х и Y. Из них извлечены независимые выборки объемов соответственно п1 и п2, по… Н0: М () = М (). (19.6) Замечание. Конечно, исправленные дисперсии, вычисленные по выборкам, обычно оказываются различными. При проверке…Лекция 20.
Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины. Проверка гипотез о нормальном, показательном и равномерном распреде-лениях по критерию Пирсона. Критерий Колмогорова. Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса.
В предыдущей лекции рассматривались гипотезы, в которых закон распределения генеральной совокупности предполагался известным. Теперь займемся проверкой гипотез о предполагаемом законе неизвестного распределения, то есть будем проверять нулевую гипотезу о том, что генеральная совокупность распределена по некоторому известному закону. Обычно статистические критерии для проверки таких гипотез называются критериями согласия.
Критерий Пирсона.
1. Проверка гипотезы о нормальном распределении. Пусть получена выборка достаточно большого объема п с большим количеством различ-ных значений вариант. Доя удобства ее…Критерий Колмогорова.
Найдем функцию эмпирического распределения Fn(x) и будем искать границы двусторон-ней критической области, определяемой условием . (20.3) А.Н.Колмогоров доказал, что в случае справедливости гипотезы Н0 распределение статистики Dn не зависит от функции…Приближенный метод проверки нормальности распределения, связанный с оценками коэффициентов асимметрии и эксцесса.
Определение 20.1.Асимметрия эмпирического распределения определяется… , (20.5)Лекция 21.
Корреляционный анализ.
Проверка гипотезы о значимости выборочного
Коэффициента корреляции.
В качестве критерия примем случайную величину , (21.1) которая при справедливости нулевой гипотезы имеет распределение Стьюдента (см. лекцию 12) с k = n – 2 степенями…Ранговая корреляция.
Пусть выборка объема п содержит независимые объекты, обладающие двумя качествен-ными признаками: А и В. Требуется выяснить степень их связи между… Расположим объекты выборки в порядке ухудшения качества по признаку А,… Теперь расположим объекты в порядке ухудшения качества по признаку В,присвоив им ранги уi , где номер i равен…Лекция 22.
Регрессионный анализ.
M (Y / x) = f (x), M ( X / y ) = φ (y). Условные средние и являются оценками условных математических ожиданий и,… =f*(x) - (22.1)Лекция 23.
Однофакторный дисперсионный анализ.
Пусть генеральные совокупности Х1, Х2,…, Хр распределены нормально и имеют одинаковую дисперсию, значение которой неизвестно. Найдем выборочные… Будем считать, что на случайную величину Х воздействует некоторый качественный… Будем считать, что количество наблюдений на каждом уровне фактора одинаково и равно q. Оформим результаты наблюдений в…Лекция 24.