Матрицы, основные понятия, действия над матрицами
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
Тема. Матрицы и определители.
Матрицы, основные понятия, действия над матрицами.
Рассмотрим таблицу вида:
 .
.
Эта таблица, состоящая из двух строк и двух столбцов, называется матрицей (причем второго порядка). Числа с двумя индексами 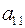 ,
, 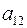 ,
, 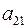 ,
,  называются элементами матрицы. Первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит данный элемент.
называются элементами матрицы. Первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит данный элемент.
Матрица, состоящая из одинакового числа строк и столбцов называется квадратной. Число строк и столбцов квадратной матрицы называется ее порядком. Квадратная матрица 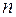 -го порядка имеет вид:
-го порядка имеет вид:
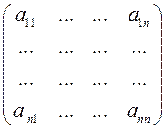 .
.
Главной диагональюквадратной матрицы называется диагональ матрицы, составленная из элементов  .
.
Симметрической матрицейназывается квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны друг другу, то есть  .
.
Пример 1: 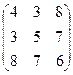
Диагональнойматрицей называется квадратная матрица, у которой все элементы, не находящиеся на главной диагонали, равны нулю.
Пример 2: 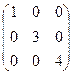 .
.
Треугольной (наддиагональной)называется квадратная матрица, если из  следует
следует  .
.
Мономиальнойназывается квадратная матрица, в каждой строке и в каждом столбце которой стоит лишь один элемент, отличный от нуля.
Единичнойназывается диагональная матрица, у которой каждый элемент, находящийся на главной диагонали, равен единице.
Пример 3:  .
.
Нулевойматрицей называется матрица, у которой все элементы равны нулю и обозначают  или
или 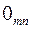 .
.
Следомквадратной матрицы 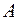 называется сумма ее диагональных элементов.
называется сумма ее диагональных элементов.
Матрицы могут быть и прямоугольными, имеющими  строк и
строк и 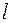 столбцов, например,
столбцов, например,  .
.
Матрица, имеющая только одну строку, называется матрицей-строкой, например,  , а матрица, имеющая только один столбец, называют матрицей-столбцом, например:
, а матрица, имеющая только один столбец, называют матрицей-столбцом, например: 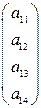 .
.
Матрицы 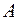 и
и 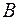 называются равными, если они имеют одно и то же число строк и одно и то же число столбцов (то есть, если они одного размера) и если при этом каждый элемент
называются равными, если они имеют одно и то же число строк и одно и то же число столбцов (то есть, если они одного размера) и если при этом каждый элемент  матрицы
матрицы 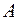 равен соответствующему элементу
равен соответствующему элементу 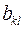 матрицы
матрицы 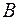 .
.
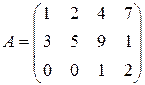 ;
; 
.
Суммойматриц 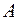 и
и 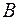 , имеющих одинаковое число строк и столбцов
, имеющих одинаковое число строк и столбцов
 ;
; 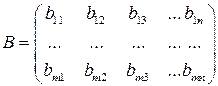 ,
,
называется третья матрица
 ,
,
каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть  .
.
Сумма матриц обозначается так 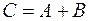 .
.
Аналогично определяется разность матриц:  , где
, где  .
.
Пример 4:  ;
; 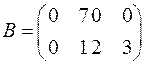 ;
;  , где
, где 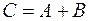 .
.
Произведение числа  на матрицу
на матрицу 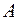 называется матрица, определяемая равенством:
называется матрица, определяемая равенством:  и получаемая из
и получаемая из 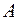 умножением всех ее элементов на
умножением всех ее элементов на  . Обозначается
. Обозначается 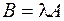 .
.
Пусть заданы две матрицы 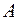 и
и 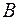 , причем число столбцов первой из них равно числу строк второй. Если
, причем число столбцов первой из них равно числу строк второй. Если
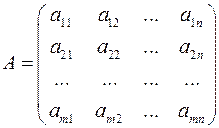 ,
, 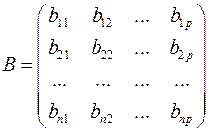 ,
,
то матрица
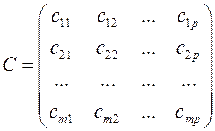 ,
,
где 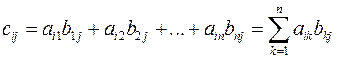 называется произведением матрицы
называется произведением матрицы 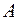 на
на 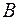 и обозначается
и обозначается  .
.
Правило умножения матрицможно сформулировать так: чтобы получить элемент, стоящий в  -ой строке и
-ой строке и  -ом столбце произведения двух матриц, нужно элементы
-ом столбце произведения двух матриц, нужно элементы  -ой строки первой матрицы умножить на соответственные элементы
-ой строки первой матрицы умножить на соответственные элементы  -го столбца второй и полученные произведения сложить. В результате умножения получается матрица, имеющая столько строк, сколько у матрицы множимого и столько столбцов, сколько у матрицы множителя.
-го столбца второй и полученные произведения сложить. В результате умножения получается матрица, имеющая столько строк, сколько у матрицы множимого и столько столбцов, сколько у матрицы множителя.
Пример 5: 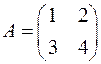 ;
;  .
.
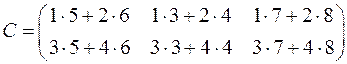 .
.
Пример 6:
 .
.
Произведение матриц зависит от порядка сомножителей. Причем, если рассматривать матрицы не квадратные, то может случиться даже, что произведение двух матриц в одном порядке будет иметь смысл, а в обратном – нет.
Но, даже для квадратных матриц произведение матриц некоммутативно, то есть не подчиняется переместительному закону.
Пример 7:  ,
,
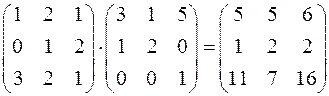 ,
,
очевидно, что  .
.
Если же  , то матрицы
, то матрицы 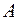 и
и 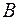 называются коммутирующими друг с другом.
называются коммутирующими друг с другом.
Пример 8:  ,
,  .
.
Единичная матрица коммутативна с любой матрицей: 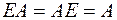 .
.
Основные свойства действий над матрицами
1) – переместительный закон 2) – сочетательный закон 3)Определители, свойства, вычисление.
или . Итак, , то есть для вычисления определителя матрицы надо из произведения… Пример: .Определители третьего порядка, определители высших порядков.
Рассмотрим матрицу порядка . . Возьмем произвольный элемент этой матрицы , удалим ту строку и тот столбец, на пересечении которых стоит этот элемент…Обратная матрица.
Если – квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая и удовлетворяющая условию . Теорема 1:для того, чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы матрица была…Ранг матрицы. Эквивалентные матрицы. Основные методы нахождения ранга матрицы.
Минором-го порядка матрицы называется определитель квадратной матрицы, получаемой из данной выделением произвольных строк и столбцов. Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.… Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным…Элементарные преобразования матрицы
1) умножение всех элементов строки (столбца) на число , 2) прибавление к элементам одной строки элементов другой строки, умноженных… 3) перемена местами строк (столбцов),Тема. Теория систем линейных уравнений.
Основные понятия и определения.
Систему уравнений:
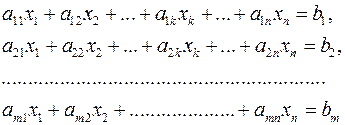 (1)
(1)
называют системой 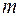 уравнений с
уравнений с 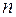 неизвестными
неизвестными  .
.
Система линейных уравнений называется совместной, если она имеет решение и несовместной, если она не имеет решений.
Совместная система линейных уравнений называется определенной если она имеет единственное решение и неопределенной если решений больше 1.
Две системы уравнений называются равносильными, если они либо обе несовместны, либо обе имеют одни и те же решения.
Элементарные преобразования, приводящие к равносильным системам:
1) перемена местами двух любых уравнений,
2) умножение обеих частей любого уравнения на произвольное число не равное нулю,
3) прибавление к обеим частям какого-либо уравнения соответствующих частей другого уравнения, умноженных на любое действительное число.
Коэффициенты системы можно записать в виде матрицы размера 

Матрица вида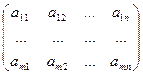 – называется основной матрицей системы.
– называется основной матрицей системы.
Матрица вида – называется расширенной матрицей системы.
– называется расширенной матрицей системы.
Неизвестные и свободные члены можно записать в виде матриц-столбцов:
 ;
;  столбец свободных членов.
столбец свободных членов.
Тогда систему можно записать в виде:
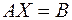 . (2)
. (2)
Система линейных уравнений называется однородной, если все свободные члены равны 0.
Решением системы линейных уравнений называется совокупность чисел 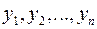 , таких, что каждое уравнение системы обращается в числовое равенство после подстановки соответствующих значений
, таких, что каждое уравнение системы обращается в числовое равенство после подстановки соответствующих значений 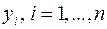 вместо
вместо  .
.