Матрицы. Действия над матрицами и их свойства
Матрицы. Действия над матрицами и их свойства.
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.Определители матриц. Свойства определителей. Миноры и алгебраические
Дополнения.
1. 2. 3. илиТ.Лапласа.Свойства.
Пусть выбраны любые k строк матрицы A. Тогда определитель матрицы A равен сумме всевозможных произведений миноров k-го порядка, расположенных в этих… Следствие:1 Широко известен частный случай теоремы Лапласа — разложение… Пусть A = (aij) — квадратная матрица размера . Пусть также задан некоторый номер строки i либо номер столбца j матрицы…Обратные матрицы и способы их вычисления.
1.Решение матричных уравнений.
АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица. Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.Система линейных алгебраических уравнений .Метод Крамера уравнений
относительна неизвестных x1, x2, ..., xn-1, xn называется системой линейных… Числа aij — коэффициенты системы, bi— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.Метод Гаусса.
ступенчато решить. Формула Крамера .Решение произвольных систем. Теорема Кронекера-Капелли.
когда ранг расширенной матрицы системы равен рангу основной матрицы. Для того чтобы система линейных уравнений была совместна, необходимо и… Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных,…Элементарные преобразования матриц. Ранг матрицы. Вычисление ранга матрицы.
1. Перестановка местами 2 параллельных рядов матрицы. 2. Умножение элементов ряда матрицы на число отличное от нуля, отличное от нуля.Балансовая модель Леонтьева.
http://archives.maillist.ru/78472/120719.html
Собственные числа и собственные векторы .
Ненулевой вектор х называется собственным вектором линейного преобразования А , соответствующим собственному числу альфа , если . Если -- двумерное или трехмерное линейное пространство, то собственный вектор… Пусть х -- собственный вектор линейного преобразования А , соответствующий собственному альфа числу и пусть а --…13.
линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, то есть коэффициенты единственной такой линейной комбинации равны нулю, множество называется линейно независимым.
Линейная независимость вектора. Базис. Прямоугольная система координат.
Система К из векторов называется линейно независимой, если равенство возможно только при , т.е. когда линейная комбинация в левой части равенства… Один вектор тоже образует систему: при — линейно зависимую, а при — линейно… Свойства линейно зависимых и линейно независимых векторов.Скалярное произведение векторов и его свойства.
равное произведению этих векторов на косинус угла между ними.Векторное произведение векторов и его свойства.
поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую. Векторным произведением вектора на вектор называется вектор , который:Смешанное произведение векторов и его свойства.
Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанногоПря Уравнение с угловым коэффициентом.
k= tg α – угловой коэффициент. Если b=0 то прямая проходит через начало координат. Уравнение примет вид Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.Уравнение прямой, проходящей через точку, в данном направлении.
Т М (х0;у0).
Подставим в это уравнение точку М Решим систему:Уравнение прямой, проходящей через 2 точки.
К (х1;у1) М (х2;у2)


Уравнение прямой в отрезках.
К (а;0); М (0;b)
Подставим точки в уравнение прямой: 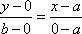

Уравнение прямой, проходящей через данную точку, перпендикулярно данному
Вектору.
М0 (х0;у0). 
Возьмем произвольную точку М (х;у).
то Нормальное уравнение прямой.Общее уравнение плоскости.
Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение определяет плоскость, проходящую через точку и имеющей нормальный вектор .Уравнение прямой в пространстве.
Уравнением прямой в пространстве, проходящей через две точки A(x0,y0,z0) и B(x1,y1,z1) называется равенство: Параметрическим уравнением прямой в пространстве, проходящей через точку…Взаимное расположение прямых и плоскостей.
параметрическими уравнениями Теорема. Пусть иЭллипс. Определение. Вывод канонического уравнения.
Т.к. MF1 + MF2 = 2a Т.к.Окружность
Уравнение 
определяет окружность радиуса R с центром C(а=0; в=0).
Если центр окружности совпадает с началом координат, то есть если , , то уравнение (1) принимает вид: