И плоскостью параллелизма.

Это линейчатые поверхности заданные двумя направляющими и дополнительным условием - образующая параллельна плоскости. Плоскость называют плоскостью параллелизма.

В качестве примера рассмотрим построение гиперболического параболоида, который в технике часто называют косой плоскостью.

 

Формула поверхности F{î( a, b, S) ( îi Ç a, b; îi÷÷ S)ý.

Направляющими примем две скрещивающиеся прямые aиbи вертикальную плоскость параллелизма S. Образующая î скользит по этим направляющим параллельно плоскости S. Построение эпюра поверхности произведем следующим образом. Построим проекции двух произвольных образующих î и î`и отметим точки пересечения с направляющими aиbкакD, E , F, G.

F2

D 2 î”2

a2

E2 b2

î 2

G2

E1 î”1

a1 F1

D1 b1

î 1

S1 G1

 

Проекции D1 E1, F1 G1 разделим на произвольное число равных частей и проведем через них горизонтальные проекции образующих. Затем построим фронтальные проекции образующих. Кривая огибающая фронтальные проекции образующих представляет собой параболу.

Подобную задачу вы будете решать в Тетради (58) на практических занятиях.

 

 

Линейчатые поверхности с тремя направляющими прямыми линиями.

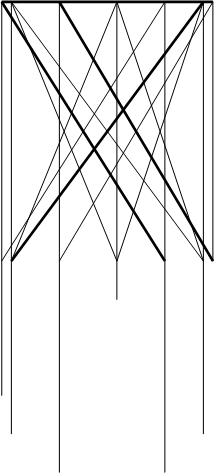
Если три направляющие b , c, d прямые линии не параллельны никакой плоскости, то скользящая по ним прямая î образует поверхность однополостного гиперболоида.

Для большей наглядности ограничим поверхность двумя плоскостями пересекающимися с поверхностью по окружностям (так как это представлено на макете). Сечение поверхности может представлять и эллипс.

Построение эпюра поверхности заключается в том, что проекции окружностей -

сечений делят на произвольное число частей . В данном случае на 12 частей.

Деление произведем циркулем начав с горизонтальных проекций сечений.

(На горизонтальной проекции они накладываются друг на друга).

Когда деление произведено как на горизонтальных, так и на фронтальных проекциях соединяем первую точку (т.1) нижней окружности с пятой точкой (т.5) верхней окружности . Строим горизонтальную, затем фронтальную проекции линии 1 - 5. Вторую точку (т.2) нижней окружности с шестой точкой (т.6) верхней окружности и т.д.. Следите за построением на доске.

Таким образом строится каркас поверхности.

Второй каркас состоит из прямых, соединяющих первую точку верхней окружности с пятой нижней окружности и т.д..

Очерк поверхности на плоскостях П 2 и П 3 - гиперболы. Он представляет собой огибающие прямые.

На макете видно, что эта поверхность может превращаться в коническую или цилиндрическую, которые являются частными случаями однополостного гиперболоида.

 

 

 

 

10 9 8 7 6 5 4

11 12 1 2 3

8 6

 

9 5

 

10 4

11 3

 

12 2

 

 

Поверхность эта не развертываемая. Часто используется в технике при строительстве водонапорных башен, телевизионных мачт и других сооружений.

 

На прошлой лекции я предлагал построить эллипс по двум осям.

В учебнике Н.С. Кузнецова на 33 странице , задача 3.(Издание 1969 г.)

 

Для построении эллипса по его осям необходимо выполнить следующее.

Проведем две окружности

с центром в точке О ,

радиусами соответственно Е

равными половине

большой и малой осей К

эллипса.

Отметим точку Е ,

пересечения произвольной

прямой ОЕ с большей окруж-

ностью и точку N ее пересечения

с меньшей окружностью.

Через точку Е проведем линию параллельно малой оси эллипса,

а через точку N линию параллельно большой оси эллипса.

Эти прямые пересекаются в точке К, принадлежащей эллипсу. Кроме найденной точки эллипсу принадлежат уже заданные четыре точки расположенные на концах большой и малой осей.

 

К следующему разу в тетради для конспектов постройте параболу.

 

ПОВЕРХНОСТИ И ТЕЛА

(продолжение)

Ц И К Л И Ч Е С К И Е П О В Е Р Х Н О С Т И

 

Циклические поверхности, могут быть образованы движением в пространстве какой - либо окружности , постоянного или переменного радиуса при перемещении ее центра по криволинейной направляющей , а плоскость окружности остается перпендикулярной к этой кривой.

 

Под это определение в качестве частного случая могут подойти уже известные нам как линейчатые поверхности кругового конуса и цилиндра.

Действительно, если направляющая прямая, а окружность постоянного радиуса,

получим цилиндр.

Если направляющая прямая, а окружность монотонно увеличивается (уменьшается) поверхность будет коническая.

Давайте в качестве примера циклической поверхности рассмотрим трубчатую поверхность переменного радиуса.

 

Для этой поверхности надо задать во-первых закон направляющей, а во вторых закон изменения радиуса окружности.

 

Зададим изменение радиуса R по длине дуги графиком

 

R

R = f (L )

 

0 L

 

Определитель трубчатой поверхности переменного радиуса будет иметь вид F[ L , R = f (L) ].

 

 

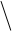
m 2 m 1

 

m (n)

j

· O

O n O2 O1

 

Если радиус постоянный, то поверхность называется просто трубчатой.

 

Если направляющей будет окружность, то при движении по ней окружности постоянного радиуса получится торовая поверхность.

Более подробно мы остановимся на рассмотрении торовых поверхностей в разделе поверхности вращения.

Давайте приведем еще пример циклической поверхности.

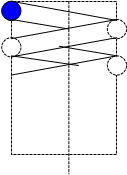
Таким примером может служить поверхность цилиндрической винтовой пружины.

 

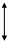
h

r

R

Подсчитаем число параметров которые задают некоторые частные виды циклических поверхностей.

Для цилиндра вращения это один параметр - радиус, для тора это два параметра это радиус окружности направляющей и радиус окружности которая перемещается в плоскости перпендикулярной направляющей, для трубчатой винтовой поверхности (поверхность пружины) это три параметра -

два радиуса (R, r ) и шаг (h).

 

П О В Е Р Х Н О С Т И В Р А Щ Е Н И Я

 

Поверхности вращения, могут быть образованы движением какой либо линии (образующей) вокруг закрепленной оси. Образующая может быть как плоской так и пространственной кривой.

Для поверхностей вращения закон движения постоянен, но разнообразны формы образующих.

В примере в качестве образующей примем кривую k состоящую из дуг двух окружностей ( R , r) , которая вращается вокруг оси j.

Любая точка кривой k описывает вокруг оси окружность лежащую в плоскости перпендикулярной оси и с центром принадлежащим оси. Эти окружности называют параллелями поверхности. Наибольшую из параллелей называют экватором, а наименьшую - горлом.

Если плоскость которой рассекают поверхность включает в себя ось, то получаемые кривые называют меридианами. Все меридианы равны между собой.

Образующая k лежит на одном из меридианов.

Меридиан расположенный во фронтальной плоскости и проектирующийся на фронтальную плоскость в натуральную величину называется главным меридианом.

Для построения главного меридиана образующую k вращают до совпадения с фронтальной плоскостью.

Если необходимо построить горизонтальную проекцию точки М принадлежащей поверхности, то достаточно провести через точку М` параллель m`1.

и найти ее горизонтальную проекцию m 1 на которой будет лежать М .

 

 

j ` ось

k`

параллель (m`1) горло(m`2) экватор (m`3)

·

M`

 

 

меридиан главный меридиан

 

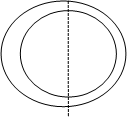
Здесь окружности m 1

концентрические. m 2

k m 3

M

j

где :

m` , m , j` , j , M`, M,

k` , k соответственно, фронтальные и горизонтальные проекции.

 

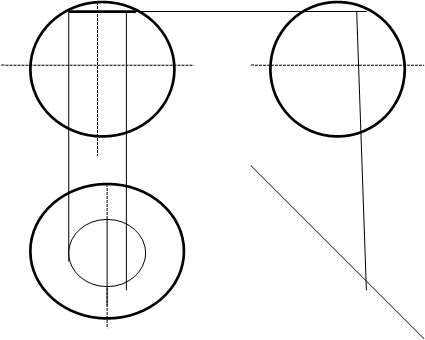
К поверхностям вращения относится сфера (тело - шар).

Сфера может быть образована вращением окружности вокруг диаметра.

F { m ( m , j ; m Ù j Ì G ; C m Ì j )( m i = m Æ j )}.

Проецируется на все плоскости ввиде равных окружностей.

Экватор шара на горизонтальную плоскость проецируется ввиде круга, а на фронтальную плоскость ввиде прямой линии параллельной оси Х.

А2 А3

 

А1

¶

 

 

Всякое сечение, параллельное экватору будет проецироваться на горизонтальную плоскость проекций ввиде окружности.

Воспользуемся этим для нахождения проекций точки А находящейся на поверхности сферы.

 

ТОР - поверхность вращения часто встречаемая в деталях машин.

Тор получается вращением окружности вокруг оси, расположенной в плоскости окружности, но не проходящей через ее центр.

Торовую поверхность вы видите на демонстрируемой модели. Это открытый тор. Окружность при вращении не пресекает ось и такой тор представляет собой кольцо.

Изобразим его основной чертеж.

 

j 2

A2

m 2

 

 

m 1 A 1

·

j 1

 

Запишем формулу этой поверхности

F{m( j , m ; m Ì Г É j; m Ë j )( m i = m Æ j)}.

 

Тор бывает закрытым. Это случай когда окружность касается оси вращения или пересекает ее. Образно эту поверхность можно представить ввиде яблока.

Формула этой поверхности Ф { m ( m, j, m Ì S É j; m Ç j) (mi = m Æ j)}.

 

Произвольная прямая пересекает тор в четырех точках. В аналитической геометрии доказывается , что тор это алгебраическая поверхность четвертого порядка.

 

j 2

m 2

A2

 

 

 

j 1 m1 A1

 

Коротко остановимся на поверхностях вращения второго порядка.

 

К ним относится эллипсоид вращения, образующийся вращением эллипса вокруг его оси. В зависимости от того какая ось эллипса выбрана осью вращения получаем сжатый или вытянутый эллипсоид вращения.

Вы уже освоили построение эллипса по двум заданным осям, теперь попробуйте изобразить в тетради основной чертеж эллипсоида вращения.

Хочу обратит ваше внимание, что в частном случае эллипс превращается в окружность , а эллипсоид в сферу.

 

ПАРАБОЛОИД ВРАЩЕНИЯ ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ПАРАБОЛЫ ВОКРУГ ЕЕ ОСИ ОZ .

j2

 

 

A2

 

j1

A1

 

ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД ВРАЩЕНИЯ МОЖЕТ БЫТЬ ОБРАЗОВАН ВРАЩЕНИЕМ ГИПЕРБОЛЫ ВОКРУГ ЕЕ МНИМОЙ ОСИ ОZ.

 

 

 

10 9 8 7 6 5 4

11 12 1 2 3

8 6

 

9 5

 

10 4

11 3

 

12 2

 

ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИД ВРАЩЕНИЯ ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ГИПЕРБОЛЫ ВОКРУГ ЕЕ ДЕЙСТВИТЕЛЬНОЙ ОСИ .

В отличие от однополостного он не является одновременно и линейчатой поверхностью. Он не может быть образован движением прямой.

Комплексный чертеж двуполостного гиперболоида прошу построить самостоятельно.