рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4).
Реферат Курсовая Конспект
Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4).
Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4). - раздел Математика, МАТЕМАТИКА Если В Уравнении (3.2) Функция ...
Если в уравнении (3.2) функция  и ее частная производная
и ее частная производная  непрерывны в некоторой области D на плоскости
непрерывны в некоторой области D на плоскости 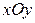 , содержащей некоторую точку
, содержащей некоторую точку 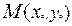 , то существует единственное решение
, то существует единственное решение 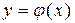 этого уравнения, удовлетворяющее начальному условию (3.4).
этого уравнения, удовлетворяющее начальному условию (3.4).
Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением. Особое решение не может быть получено из формулы общего решения (общего интеграла) ни при каких числовых значениях произвольной постоянной.
Например, одним из решений уравнения  является функция
является функция 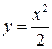 - одно из его частных решений. Формула
- одно из его частных решений. Формула 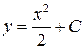 , где С – произвольное действительное число, дает множество всех решений этого уравнения, т.е. является его общим решением. Функция
, где С – произвольное действительное число, дает множество всех решений этого уравнения, т.е. является его общим решением. Функция 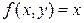 и ее частная производная
и ее частная производная  определены и непрерывны во всей плоскости
определены и непрерывны во всей плоскости 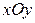 . Потому через каждую точку этой плоскости проходит единственная интегральная кривая – частное решение данного дифференциального уравнения. Например, Задача Коши:
. Потому через каждую точку этой плоскости проходит единственная интегральная кривая – частное решение данного дифференциального уравнения. Например, Задача Коши:
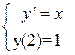
имеет единственное решение  , найденное из общего решения данного дифференциального уравнения при подстановке в него начальных значений:
, найденное из общего решения данного дифференциального уравнения при подстановке в него начальных значений: 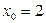 ,
, 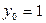 , что позволяет определить конкретное значение произвольной постоянной
, что позволяет определить конкретное значение произвольной постоянной 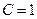 .
.
Дифференциальные уравнения с разделяющимися переменными
Если в уравнении (2) его правая часть имеет вид 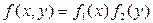 , то в этом случае оно называется уравнением с разделяющимися переменными и решается методом “разделения” переменных.
, то в этом случае оно называется уравнением с разделяющимися переменными и решается методом “разделения” переменных.
В частности, если уравнение (2) имеет вид  , т.е.
, т.е. 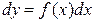 , то в результате интегрирования обеих частей этого уравнения его общее решение дается формулой
, то в результате интегрирования обеих частей этого уравнения его общее решение дается формулой 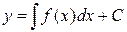 , где С – произвольная постоянная.
, где С – произвольная постоянная.
3.1). Пусть 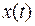 - количество радиоактивного вещества - радия еще не распавшегося к моменту времени t. Установлено, что скорость радиоактивного распада
- количество радиоактивного вещества - радия еще не распавшегося к моменту времени t. Установлено, что скорость радиоактивного распада  пропорциональна количеству вещества с коэффициентом пропорциональности k. При условии, что в начальный момент времени
пропорциональна количеству вещества с коэффициентом пропорциональности k. При условии, что в начальный момент времени 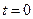 масса радия была
масса радия была 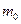 , выяснить период его полураспада – промежуток времени, за который распадается половина его первоначальной массы.
, выяснить период его полураспада – промежуток времени, за который распадается половина его первоначальной массы.
Решение. Поиск ответа на поставленный в этом Примере вопрос сводится к решению Задачи Коши:
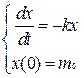 (3.5) – (3.6)
(3.5) – (3.6)
Знак минус в правой части уравнения (3.5) обусловлен убыванием функции x(t) c течением времени. Уравнение (3.5) является уравнением с разделяющимися переменными. Умножая обе его части на 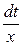 , получаем уравнение с разделенными переменными
, получаем уравнение с разделенными переменными 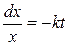 . Интегрируя обе части которого получаем
. Интегрируя обе части которого получаем  , или
, или  . Т.е. общее решение уравнения (3.5) имеет вид
. Т.е. общее решение уравнения (3.5) имеет вид 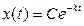 . Постоянную С (С> 0) определим так, чтобы было выполнено начальное условие (6):
. Постоянную С (С> 0) определим так, чтобы было выполнено начальное условие (6): 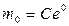 , т.е.
, т.е.  .
.
Таким образом, функция 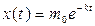 является решением задачи (3.5) – (3.6).
является решением задачи (3.5) – (3.6).
Единица измерения времени – год. Период полураспада 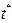 находим, решая уравнение
находим, решая уравнение 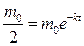 . Итак,
. Итак, 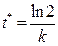 . В частности, так как для радия
. В частности, так как для радия 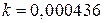 , то
, то  лет.
лет.
3.2). Решить Задачу Коши:
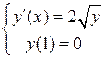 (3.7)-(3.8)
(3.7)-(3.8)
Решение. Функция 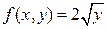 определена и непрерывна в области
определена и непрерывна в области
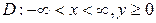 . Производная
. Производная 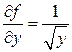 не определена в точках оси
не определена в точках оси 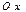 , поэтому в любой окрестности точки (1,0) не выполняются условия Теоремы о существовании и единственности решения Задачи Коши. Действительно, с одной стороны, разделяя переменные в уравнении (7) получим
, поэтому в любой окрестности точки (1,0) не выполняются условия Теоремы о существовании и единственности решения Задачи Коши. Действительно, с одной стороны, разделяя переменные в уравнении (7) получим 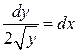 и, проинтегрировав обе части последнего равенства, находим общее решение в виде
и, проинтегрировав обе части последнего равенства, находим общее решение в виде 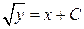 . Геометрически – это множество правых ветвей парабол
. Геометрически – это множество правых ветвей парабол 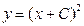 (т.к.
(т.к. 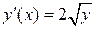
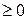 ) с вершинами в точках (-С,0). С другой стороны, исключаемая при разделении переменных в уравнении (3.7) функция
) с вершинами в точках (-С,0). С другой стороны, исключаемая при разделении переменных в уравнении (3.7) функция 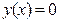 , является очевидным решением этого уравнения, которое должно быть названо особым. Ни при каких значениях произвольной постоянной С оно не может быть получено из формулы общего решения. Таким образом, через точку (1,0) проходят по крайней мере две интегральные кривые:
, является очевидным решением этого уравнения, которое должно быть названо особым. Ни при каких значениях произвольной постоянной С оно не может быть получено из формулы общего решения. Таким образом, через точку (1,0) проходят по крайней мере две интегральные кривые: 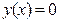 и
и 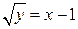 . Кроме того, интегральными кривыми являются также линии АОBD,
. Кроме того, интегральными кривыми являются также линии АОBD, 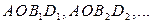 при любых
при любых 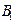 и
и  ,
, 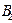 и
и 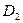 , … . Итак, поставленная задача Коши (3.7) – (3.8) имеет бесконечное множество решений.
, … . Итак, поставленная задача Коши (3.7) – (3.8) имеет бесконечное множество решений.

Рис2.1
Задания для самостоятельного решения
Найти общие решения дифференциальных уравнений
3.1. 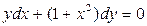 . 3.2.
. 3.2.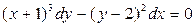 . 3.3.
. 3.3.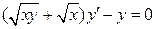 .
.
Найти решение задачи Коши.
3.4.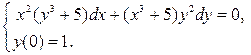 3.5.
3.5. .
.
3.6. 
Найти общее и особые решения уравнения.
3.7.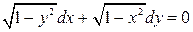
Ответы.
3.1. 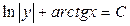 . 3.2.
. 3.2.  . 3.3
. 3.3  .
.
3.4. 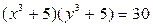 . 3.5.
. 3.5. 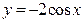 . 3.6.
. 3.6.  .
.
3.7.  .
.
Однородные дифференциальные уравнения
Функция 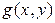 называется однородной порядка однородности
называется однородной порядка однородности  , если для любого числа
, если для любого числа 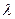 (такого, что
(такого, что 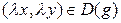 ) выполняется условие:
) выполняется условие:  . Например,
. Например, 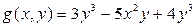 - однородная функция третьего порядка однородности.
- однородная функция третьего порядка однородности.
Уравнение (3) называется однородным дифференциальным уравнением,если коэффициенты 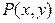 и
и 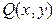 являются однородными функциями одинакового порядка однородности. Уравнение в виде (2) также может быть названо однородным, если
являются однородными функциями одинакового порядка однородности. Уравнение в виде (2) также может быть названо однородным, если  - однородная функция нулевого порядка однородности (
- однородная функция нулевого порядка однородности ( ).
).
Однородное уравнение приводится к уравнению с разделяющимися переменными введением новой искомой функции
 . (3.9)
. (3.9)
3.3). Найти общее решение уравнения
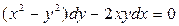 . (3.10)
. (3.10)
Решение. Функции 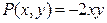 и
и 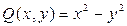 — однородные функции второго порядка однородности, поэтому данное уравнение является однородным. Используя замену (3.9), из которой
— однородные функции второго порядка однородности, поэтому данное уравнение является однородным. Используя замену (3.9), из которой  , а
, а 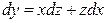 , записываем данное уравнение в виде
, записываем данное уравнение в виде
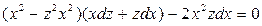 .
.
Разделяя переменные, получим 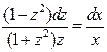 . Интегрируя обе части последнего равенства и учитывая, что
. Интегрируя обе части последнего равенства и учитывая, что 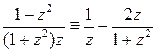 , находим
, находим 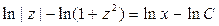 , откуда имеем
, откуда имеем 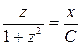 . Возвращаясь к исходной функции
. Возвращаясь к исходной функции  , получаем общий интеграл уравнения (3.10) в виде
, получаем общий интеграл уравнения (3.10) в виде 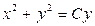 . Интегральные кривые уравнения (3.10) представляют собой семейство окружностей с центрами на оси
. Интегральные кривые уравнения (3.10) представляют собой семейство окружностей с центрами на оси  , проходящих через начало координат.
, проходящих через начало координат.
Задания для самостоятельного решения
3.8.  3.9.
3.9. 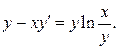 3.10.
3.10. 
3.11. 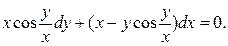 3.12.
3.12.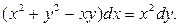
3.13. 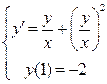 . 3.14.
. 3.14. 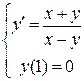 .
.
Ответы.
3.8.  . 3.9.
. 3.9. 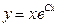 . 3.10.
. 3.10. 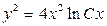 . 3.11.
. 3.11. 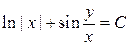 .
.
3.12. 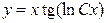 . 3.13.
. 3.13.  . 3.14.
. 3.14. 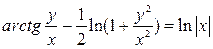 .
.
Линейные уравнения первого порядка. Уравнение Бернулли
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее первой производной:
 . (3.11)
. (3.11)
Здесь  и
и 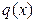 — заданные непрерывные функции. Уравнение (3.11), в котором
— заданные непрерывные функции. Уравнение (3.11), в котором 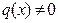 , называется линейным неоднородным, а уравнение
, называется линейным неоднородным, а уравнение
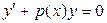 (3.12)
(3.12)
называется линейным однородным, соответствующим данному неоднородному уравнению (3.11).
Первый способ решения линейного неоднородного уравнения – метод подстановки. Он заключается в том, чтобы искать функцию 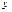 в виде произведения двух функций
в виде произведения двух функций
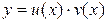 . (3.13)
. (3.13)
3.4). Решить уравнение
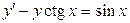 . (3.14)
. (3.14)
Решение. Это уравнение является линейным, поэтому его решение ищем с помощью подстановки (13), из которой находим 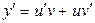 . В результате уравнение (3.14) приобретает вид
. В результате уравнение (3.14) приобретает вид 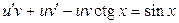 , или
, или
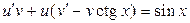 . (3.15)
. (3.15)
Для упрощения последнего равенства сомножитель 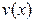 будем искать таким, чтобы
будем искать таким, чтобы  (равенство нулю множителя при функции
(равенство нулю множителя при функции 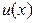 в уравнении (3.15)). Заметим, что это последнее условие является однородным уравнением, соответствующим линейному неоднородному уравнению (3.14). Кроме того, как и любое уравнение вида (3.12), оно является уравнением с разделяющимися переменными:
в уравнении (3.15)). Заметим, что это последнее условие является однородным уравнением, соответствующим линейному неоднородному уравнению (3.14). Кроме того, как и любое уравнение вида (3.12), оно является уравнением с разделяющимися переменными: 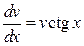 ,
,  ,
, 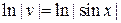 ,
, 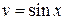 . Найденная функция является частным решением уравнения. В данном случае достаточно иметь хотя бы одну функцию
. Найденная функция является частным решением уравнения. В данном случае достаточно иметь хотя бы одну функцию 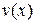 , обращающую в ноль выражение в круглой скобке в уравнении (3.15). Далее, подставляя найденный сомножитель
, обращающую в ноль выражение в круглой скобке в уравнении (3.15). Далее, подставляя найденный сомножитель 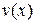 в уравнение (3.15), получаем
в уравнение (3.15), получаем 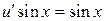 , отсюда
, отсюда  ,
, 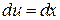 ,
, 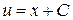 . Заметим, что при определении второго сомножителя константа интегрирования обязательно учитывается. И, наконец, по формуле (3.13) записываем общее решение уравнения (3.14):
. Заметим, что при определении второго сомножителя константа интегрирования обязательно учитывается. И, наконец, по формуле (3.13) записываем общее решение уравнения (3.14): 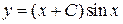 .
.
Второй способ решения линейного неоднородного уравнения называется методом вариации произвольной постоянной. Он заключается в том, что вначале решается однородное уравнение (3.12), которое, как мы отметили, является уравнением с разделяющимися переменными. Легко получить его общее решение: 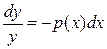 ,
, 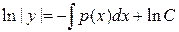 ,
, 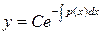 . Далее, решение уравнения (3.11) ищем, полагая
. Далее, решение уравнения (3.11) ищем, полагая 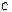 некоторой функцией переменной
некоторой функцией переменной 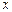 :
: 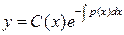 . Таким образом, при решении неоднородного уравнения (3.11) мы варьируем, меняем постоянную, входящую в общее решение уравнения (3.12).
. Таким образом, при решении неоднородного уравнения (3.11) мы варьируем, меняем постоянную, входящую в общее решение уравнения (3.12).
3.5). Решить уравнение
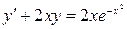 . (3.16)
. (3.16)
Решение. Разделяя переменные в линейном однородном уравнении 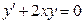 , соответствующем данному уравнению (3.16), получим:
, соответствующем данному уравнению (3.16), получим: 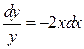 ,
, 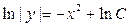 ,
, 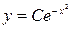 . Общее решение уравнения (3.16) будем искать в виде
. Общее решение уравнения (3.16) будем искать в виде
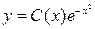 , (3.17)
, (3.17)
где 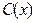 — неизвестная функция, для определения которой подставим
— неизвестная функция, для определения которой подставим 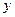 в виде (3.17) в уравнение (3.16):
в виде (3.17) в уравнение (3.16): 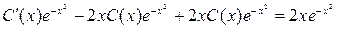 , т. е.
, т. е. 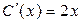 и
и 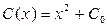 . Подставив найденную таким образом функцию
. Подставив найденную таким образом функцию 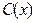 в (3.17), получим общее решение уравнения (3.16):
в (3.17), получим общее решение уравнения (3.16): 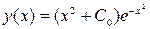 .
.
Уравнение  , где
, где  и
и 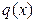 — заданные непрерывные функции, а показатель степени
— заданные непрерывные функции, а показатель степени  отличен от нуля (при
отличен от нуля (при  получаем рассмотренное выше линейное неоднородное уравнение) и от единицы (при
получаем рассмотренное выше линейное неоднородное уравнение) и от единицы (при  приводя подобные слагаемые и получаем линейное однородное уравнение), называется уравнением Бернулли. Оно решается теми же способами, что и линейное неоднородное уравнение.
приводя подобные слагаемые и получаем линейное однородное уравнение), называется уравнением Бернулли. Оно решается теми же способами, что и линейное неоднородное уравнение.
3.6). Решить уравнение
 . (3.18)
. (3.18)
Решение. Разделив обе части этого уравнения на 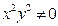 , убеждаемся, что это — уравнение Бернулли:
, убеждаемся, что это — уравнение Бернулли: 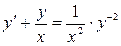 . Здесь
. Здесь 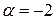 . Воспользуемся подстановкой (3.13):
. Воспользуемся подстановкой (3.13):
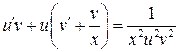 . (3.19)
. (3.19)
Вспомогательную функцию 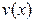 находим из условия
находим из условия  . Разделив в этом уравнении переменные, получим
. Разделив в этом уравнении переменные, получим  ,
, 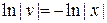 , откуда имеем частное решение
, откуда имеем частное решение 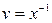 , подставляя которое в (3.19), получаем уравнение для нахождения функции
, подставляя которое в (3.19), получаем уравнение для нахождения функции 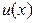 :
:  . Проинтегрировав последнее равенство, найдем
. Проинтегрировав последнее равенство, найдем 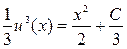 , или
, или 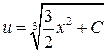 . Следовательно, общее решение уравнения (3.18) имеет вид
. Следовательно, общее решение уравнения (3.18) имеет вид  .
.
Задания для самостоятельного решения.
3.15. 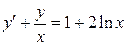 . 3.16.
. 3.16. 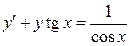 . 3.17.
. 3.17. 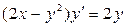 .
.
3.18. 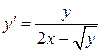 . 3.19.
. 3.19.  . 3.20.
. 3.20. 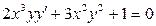 .
.
3.21.  . 3.22.
. 3.22.  . 3.23.
. 3.23. .
.
3.24.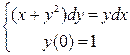 . 3.25.
. 3.25.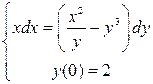 . .
. .
Ответы.
3.15. 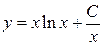 . 3.16.
. 3.16. 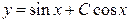 . 3.17.
. 3.17. 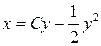 . 3.18.
. 3.18. 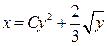 .
.
3.19. 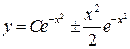 . 3.20.
. 3.20. 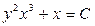 . 3.21.
. 3.21.  . 3.22.
. 3.22. 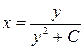 .
.
3.23.  . 3.24.
. 3.24. 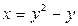 . 3.25.
. 3.25. 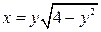 .
.
Уравнения в полных дифференциалах.
Дифференциальное уравнение (3.3), называется уравнением в полных дифференциалах, если его левая часть является дифференциалом первого порядка некоторой функции двух переменных  , т. е.
, т. е. 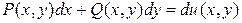 . Для того, чтобы уравнение (3.3) было уравнением в полных дифференциалах, необходимо и достаточно выполнение условия для коэффициентов
. Для того, чтобы уравнение (3.3) было уравнением в полных дифференциалах, необходимо и достаточно выполнение условия для коэффициентов  и
и 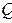 :
:
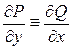 , (3.20)
, (3.20)
тогда уравнение (3.3) принимает вид 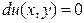 , и его общий интеграл легко записывается в виде:
, и его общий интеграл легко записывается в виде: 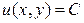 , где
, где 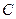 — произвольная постоянная.
— произвольная постоянная.
3.7). Решить уравнение 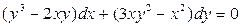 .
.
Решение. Условие (3.20) выполнено, т.к. 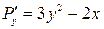 и
и 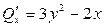 . Значит, данное уравнение является уравнением в полных дифференциалах. Следовательно, надо найти функцию
. Значит, данное уравнение является уравнением в полных дифференциалах. Следовательно, надо найти функцию  такую, что
такую, что 
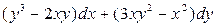 , т.е.
, т.е.
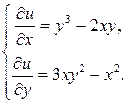 (3.21)
(3.21)
Проинтегрируем первое уравнение системы (3.21): 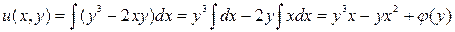 . Здесь мы учли, что при интегрировании по
. Здесь мы учли, что при интегрировании по  переменная
переменная 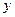 рассматривается как константа. По этой же причине постоянная интегрирования записана как некая произвольная функция
рассматривается как константа. По этой же причине постоянная интегрирования записана как некая произвольная функция 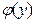 . Определим эту функцию, воспользовавшись вторым уравнением системы (3.21):
. Определим эту функцию, воспользовавшись вторым уравнением системы (3.21):
 ,
,
откуда 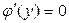 . Выберем в качестве решения последнего уравнения
. Выберем в качестве решения последнего уравнения 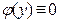 , тогда
, тогда  , и общий интеграл исходного уравнения имеет вид
, и общий интеграл исходного уравнения имеет вид 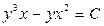 .
.
Задания для самостоятельного решения.
3.26. 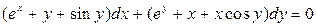 .
.
3.27.  .
.
3.28.  . 3.29.
. 3.29.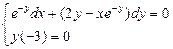 .
.
3.30.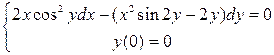 . 3.31.
. 3.31.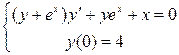 .
.
Ответы
3.26. 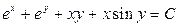 . 3.27.
. 3.27. 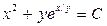 . 3.28.
. 3.28. 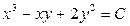 .
.
3.29. 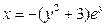 . 3.30.
. 3.30.  . 3.31.
. 3.31. 
3.3.Дифференциальные уравнения высших порядков, допускающие понижения порядка
Дифференциальное уравнение 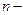 го порядка имеет следующий общий вид
го порядка имеет следующий общий вид
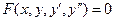 .
.
Его общее решение 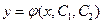 содержит две произвольные постоянные
содержит две произвольные постоянные 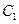 и
и 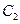 .
.
Рассмотрим несколько типов уравнений второго порядка, допускающих понижение порядка.
I. Простейший частный случай уравнения 2-го порядка записывается так: . Искомая функция здесь находится последовательным двукратным интегрированием.
. Искомая функция здесь находится последовательным двукратным интегрированием.
3.8). 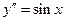 . Запишем это уравнение в виде
. Запишем это уравнение в виде 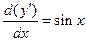 . Умножая обе его части на
. Умножая обе его части на  , имеем
, имеем 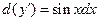 . И после интегрирования
. И после интегрирования 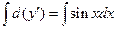 , получаем
, получаем 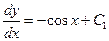 , где
, где 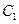 - произвольная постоянная. После умножения обеих частей последнего равенства на
- произвольная постоянная. После умножения обеих частей последнего равенства на  и интегрирования получаем общее решения данного уравнения
и интегрирования получаем общее решения данного уравнения  . Здесь
. Здесь 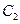 - вторая произвольная постоянная.
- вторая произвольная постоянная.
II. Уравнение не содержит искомой функции: 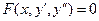 . Порядок такого уравнения может быть понижен заменой, введением новой искомой функции
. Порядок такого уравнения может быть понижен заменой, введением новой искомой функции 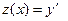 .
.
3.9). Найти общее решение уравнения:  .
.
Решение. Обозначим 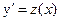 . Тогда
. Тогда 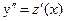 , и данное уравнение теперь выглядит так:
, и данное уравнение теперь выглядит так:
 ,
,
т.е. благодаря используемой здесь замене удалось исходное уравнение второго порядка преобразовать к дифференциальному уравнению первого порядка, добиться понижения порядка исходного уравнения. Разделяя переменные и интегрируя, из последнего равенства получаем: 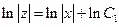 , т.е.
, т.е. 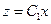 , а, значит,
, а, значит, 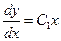 . Разделение переменных и интегрирование последнего равенства дает общее решение исходного уравнения:
. Разделение переменных и интегрирование последнего равенства дает общее решение исходного уравнения: 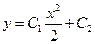 .
.
III. Уравнение не содержит независимой переменной  :
: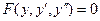 . Рассматривая
. Рассматривая 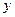 здесь как независимую переменную, можем на единицу понизить порядок уравнения введением в него новой искомой функции
здесь как независимую переменную, можем на единицу понизить порядок уравнения введением в него новой искомой функции 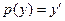 . При этом
. При этом 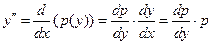 .
.
3.10). Решить уравнение: 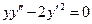 .
.
Решение. Пользуясь только что указанной подстановкой, понизим порядок данного уравнения: 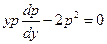 , или
, или  . Отсюда получаем два уравнения:
. Отсюда получаем два уравнения:
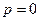 ,
,  .
.
Первое из них дает  , т.е.
, т.е.  . Второе уравнение решается разделением переменных, откуда
. Второе уравнение решается разделением переменных, откуда 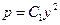 . Но, так как
. Но, так как  , то, разделяя переменные, получаем
, то, разделяя переменные, получаем  , т.е.
, т.е.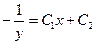 , или
, или  . Отметим, что найденное ранее решение
. Отметим, что найденное ранее решение  содержится в предыдущей функции при
содержится в предыдущей функции при 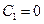 .
.
Задания для самостоятельного решения.
3.32. . 3.33.
. 3.33.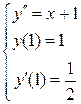 . 3.34.
. 3.34.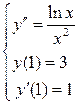 3.35.
3.35.  .
.
3.36. 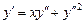 . 3.37.
. 3.37.  . 3.38.
. 3.38. 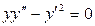 .
.
3.39. 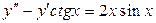 . 3.40.
. 3.40.  . 3.41.
. 3.41.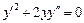 . 3.42.
. 3.42. 
3.43. . 3.44.
. 3.44. 
.
Ответы
3.32. 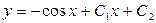 . 3.33.
. 3.33. 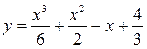 . 3.34.
. 3.34. 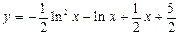 .
.
3.35. 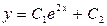 . 3.36.
. 3.36. 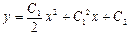 ,
, 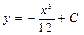 . 3.37.
. 3.37. 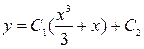 .
.
3.38. 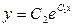 . 3.39.
. 3.39. 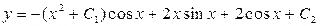 .
.
3.40. 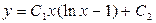 . 3.41.
. 3.41. 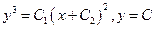 . 3.42.
. 3.42.  .
.
3.43. 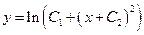 . 3.44.
. 3.44. 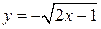 .
.
3.4.Линейные дифференциальные уравнения.
Линейным дифференциальным уравнением 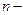 го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных, оно имеет следующий общий вид:
го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных, оно имеет следующий общий вид:
 (3.22)
(3.22)
Если заданные коэффициенты 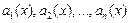 и правая часть
и правая часть 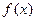 - функции, непрерывные на некотором интервале
- функции, непрерывные на некотором интервале 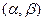 , то уравнение (3.22) имеет единственное решение
, то уравнение (3.22) имеет единственное решение  , определенное на интервале
, определенное на интервале 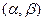 и удовлетворяющее начальным условиям
и удовлетворяющее начальным условиям
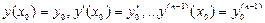 , (3.23)
, (3.23)
где 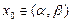 , а
, а 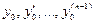 - любые действительные числа.
- любые действительные числа.
Уравнение (3.22), в котором 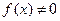 тождественно на
тождественно на 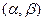 , называется линейным неоднородным дифференциальным уравнением (ЛНДУ), а уравнение
, называется линейным неоднородным дифференциальным уравнением (ЛНДУ), а уравнение
 (3.24)
(3.24)
- линейным однородным дифференциальным уравнением (ЛОДУ).
Общее решение уравнения (3.24) имеет вид
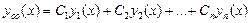 , (3.25)
, (3.25)
где 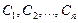 - произвольные постоянные, а
- произвольные постоянные, а 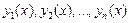 -
- 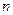 линейно независимых частных решений уравнения (3.24), составляющих так называемую фундаментальную систему решений ЛОДУ.
линейно независимых частных решений уравнения (3.24), составляющих так называемую фундаментальную систему решений ЛОДУ.
Критерием (т.е. необходимым и достаточным условием) линейной независимости 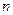 частных решений
частных решений 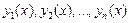 уравнения (3.24) является условие необращения в ноль на интервале
уравнения (3.24) является условие необращения в ноль на интервале 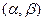 определителя Вронского для этих функций:
определителя Вронского для этих функций:
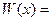

 (3.26)
(3.26)
Общее решение ЛНДУ (3.22) имеет следующий вид:
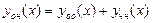 . (3.27)
. (3.27)
Здесь 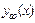 - общее решение ЛОДУ (3.24), соответствующего данному ЛНДУ (3.22), а
- общее решение ЛОДУ (3.24), соответствующего данному ЛНДУ (3.22), а 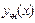 - некоторое частное решение ЛНДУ (3.22). Представление (3.27) вместе с формулой (3.25) описывает структуру общего решения ЛНДУ.
- некоторое частное решение ЛНДУ (3.22). Представление (3.27) вместе с формулой (3.25) описывает структуру общего решения ЛНДУ.
Линейные однородные уравнения с постоянными коэффициентами
Линейное однородное уравнение второго порядка с постоянными коэффициентами выглядит так:
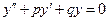 . (3.28)
. (3.28)
Здесь коэффициенты 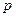 и
и 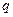 - некоторые действительные числа.
- некоторые действительные числа.
Определим значение параметра 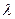 так, чтобы функция
так, чтобы функция 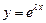 удовлетворяла равенству (3.28), т.е. являлась решением этого уравнения. Для этого подставим эту функцию и ее производные
удовлетворяла равенству (3.28), т.е. являлась решением этого уравнения. Для этого подставим эту функцию и ее производные 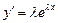 ,
, 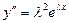 в равенство (3.28) . Получим
в равенство (3.28) . Получим 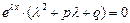 , откуда выводим равенство
, откуда выводим равенство
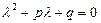 , (3.29)
, (3.29)
называемое характеристическим уравнением линейного однородного дифференциального уравнения (3.28). Уравнение (3.29) является квадратным уравнением и имеет 2 корня (действительных различных, действительных равных, или 2 комплексно - сопряженных). Каждому корню 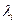 этого уравнения соответствует отдельное частное решение
этого уравнения соответствует отдельное частное решение  ,
,  В совокупности этот набор решений составляет фундаментальную систему решений уравнения (3.28), с помощью которой по формуле (3.25) можно записать общее решение этого уравнения.
В совокупности этот набор решений составляет фундаментальную систему решений уравнения (3.28), с помощью которой по формуле (3.25) можно записать общее решение этого уравнения.
Таким образом, алгеброй определяется характер решений линейных дифференциальных уравнений, а, значит, и те физические, химические, и.т.д. процессы, которые ими описываются.
Возможные при решении уравнения (3.28) случаи представлены в следующей таблице.
Таблица 2.
| № | Корни характеристического уравнения 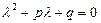
| Фундаментальная система решений диффер. уравнения (3.29) | Вид общего решения уравнения
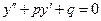
|
 и и  - действительные различные числа - действительные различные числа
| 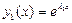 , , 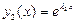
| 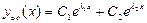
| |
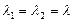 - двукратный корень - двукратный корень
| 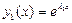 , , 
| 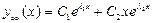
| |
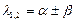 - комплексно сопряженные корни - комплексно сопряженные корни
| 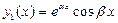 , ,
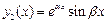
|

|
3.11). Решить уравнение  .
.
Решение. Характеристическое уравнение, соответствующее данному дифференциальному, имеет вид 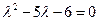 . Корни
. Корни 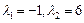 этого уравнения действительны и различны. Им отвечают два частных решения
этого уравнения действительны и различны. Им отвечают два частных решения 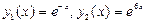 , с помощью которых записываем общее решение данного уравнения
, с помощью которых записываем общее решение данного уравнения 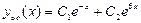 .
.
3.12). Решить уравнение 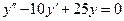 .
.
Решение. Характеристическое уравнение для данного дифференциального имеет вид: 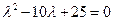 , или
, или 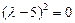 . Т.е. его корни
. Т.е. его корни 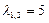 . В соответствии со случаем 2 Таблицы 2 частными решениями данного дифференциального уравнения, составляющими его фундаментальную систему решений, являются функции
. В соответствии со случаем 2 Таблицы 2 частными решениями данного дифференциального уравнения, составляющими его фундаментальную систему решений, являются функции  , а его общее решение имеет вид
, а его общее решение имеет вид 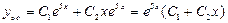 .
.
3.13). Решить уравнение 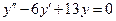 .
.
Решение. Характеристическое уравнение для данного дифференциального выглядит так: 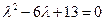 . Оно имеет пару комплексно - сопряженных корней
. Оно имеет пару комплексно - сопряженных корней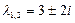 . Здесь
. Здесь 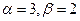 . Соответствующие частные решения
. Соответствующие частные решения 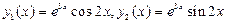 составляют фундаментальную систему решений данного дифференциального уравнения, а его общее решение записывается так:
составляют фундаментальную систему решений данного дифференциального уравнения, а его общее решение записывается так: 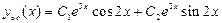 .
.
Задания для самостоятельного решения
3.45.  . 3.46.
. 3.46.  . 3.47.
. 3.47. 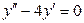 . 3.48.
. 3.48.  .
.
3.49.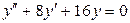 . 3.50.
. 3.50. . 3.51.
. 3.51.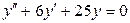 . 3.52.
. 3.52.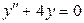 .
.
Ответы
3.45.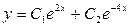 .3.46.
.3.46.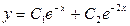 . 3.47.
. 3.47. . 3.48.
. 3.48.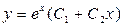 .
.
3.49.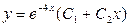 . 3.50.
. 3.50. . . 3.51.
. . 3.51.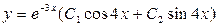 . 3.52.
. 3.52.  .
.
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
В том случае, когда в ЛНДУ второго порядка, т.е. в уравнении (22) при 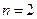 , коэффициенты в левой его части являются постоянными, оно имеет вид
, коэффициенты в левой его части являются постоянными, оно имеет вид
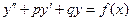 (3.30)
(3.30)
Следуя формуле (3.27), сначала (с помощью характеристического уравнения) необходимо решить соответствующее ему ЛОДУ: 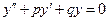 . Второе слагаемое в формуле (3.27), некоторое частное решение
. Второе слагаемое в формуле (3.27), некоторое частное решение 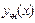 уравнения (3.30), может быть записано в виде функции того же типа, что и правая часть -
уравнения (3.30), может быть записано в виде функции того же типа, что и правая часть - 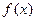 , если она имеет специальный вид, приведенный в следующей таблице.
, если она имеет специальный вид, приведенный в следующей таблице.
Таблица 3.
| № | 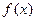 - правая часть ЛНДУ (30) - правая часть ЛНДУ (30)
| Корни характеристического уравнения (3.29) | Вид частного решения 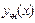
|
| I | 
| 1. Число 0 не является корнем характеристического уравнения | 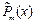
|
2. Число 0 -корень характеристического уравнения кратности 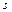
| 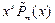
| ||
| II | 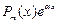
| 1. Число 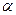 не является корнем характеристического уравнения не является корнем характеристического уравнения
| 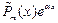
|
2.Число 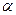 -корень характеристического уравнения кратности -корень характеристического уравнения кратности 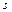
| 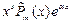
| ||
| III | 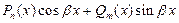
| 1. Числа 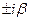 не являются корнями характеристического уравнения не являются корнями характеристического уравнения
|  , ,
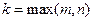
|
2. Числа 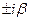 являются корнями характеристического уравнения являются корнями характеристического уравнения
|  , ,
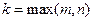
| ||
| IV | 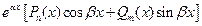
| 1. Числа 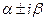 не являются корнями не являются корнями
| 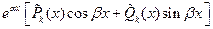 , ,
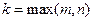
|
2. Числа 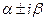 являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 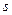
| 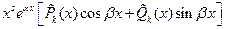 , ,
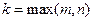
|
Указанные в этой таблице 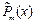 ,
, 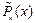 ,
, 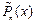 ,
, 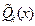 ,
,  - многочлены с неопределенными коэффициентами.
- многочлены с неопределенными коэффициентами.
3.14). Решить уравнение 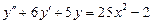 .
.
Решение. Однородное уравнение, соответствующее данному неоднородному имеет вид:
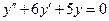 . Его характеристическое уравнение
. Его характеристическое уравнение  имеет корни
имеет корни 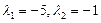 , которым соответствуют частные решения
, которым соответствуют частные решения 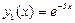 ,
,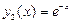 . По формуле (25)
. По формуле (25) 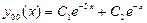 . Второе слагаемое в формуле (3.27) , т.е. некоторое частное решение
. Второе слагаемое в формуле (3.27) , т.е. некоторое частное решение 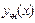 данного ЛНДУ, в соответствии с приведенной выше Таблицей 3, раздел I(1), является функцией подобной правой части
данного ЛНДУ, в соответствии с приведенной выше Таблицей 3, раздел I(1), является функцией подобной правой части 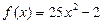 . А, так как среди корней характеристического уравнения нет числа
. А, так как среди корней характеристического уравнения нет числа  , то
, то
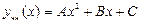 , (3.31)
, (3.31)
где 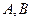 и
и 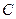 - неопределенные пока коэффициенты. Найдем эти числа, подставляя функцию (3.31) в исходное уравнение, которому она должна удовлетворять. Так как
- неопределенные пока коэффициенты. Найдем эти числа, подставляя функцию (3.31) в исходное уравнение, которому она должна удовлетворять. Так как 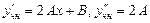 , то получим равенство
, то получим равенство 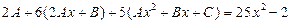 , или
, или
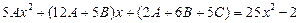 .
.
Приравнивая коэффициенты при одинаковых степенях  в обеих частях последнего равенства, получим систему из трех уравнений с тремя неизвестными
в обеих частях последнего равенства, получим систему из трех уравнений с тремя неизвестными 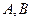 и
и 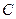 .
.
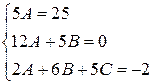
Откуда  . Поэтому
. Поэтому  , а общее решение данного уравнения:
, а общее решение данного уравнения: 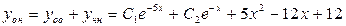 .
.
3.15). Решить уравнение 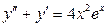 .
.
Решение. Сначала решим соответствующее однородное уравнение: 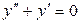 . Его характеристическое уравнение
. Его характеристическое уравнение  , или
, или 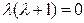 , имеет корни
, имеет корни  . Поэтому общее решение однородного уравнения записывается так:
. Поэтому общее решение однородного уравнения записывается так: 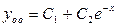 . Так как число
. Так как число 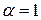 не является корнем характеристического уравнения, то в соответствии с разделом II (1) Таблицы 3 частное решение данного уравнения имеет вид
не является корнем характеристического уравнения, то в соответствии с разделом II (1) Таблицы 3 частное решение данного уравнения имеет вид 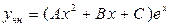 . Для нахождения коэффициентов
. Для нахождения коэффициентов 
– Конец работы –
Эта тема принадлежит разделу:
МАТЕМАТИКА
Федеральное государственное образовательное бюджетное... учреждение высшего профессионального образования... Московский технический университет связи и информатики...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4).
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов