Элементы симметрии и основы теории групп. Решетки Бравэ
Элементы симметрии и основы теории групп.
Решетки Бравэ
ВВЕДЕНИЕ
Курс лекций называется «Кристаллофизика». Основным предметом изучения является кристалл и связь закономерностей строения кристалла с проявлением физических свойств. Кристаллофизика является теоретической основой таких областей техники, как полупроводниковая электроника, пьезотехника, квантовая электроника, нелинейная оптика, и как наука о связи физических свойств кристалла с их симметрией возникла в начале нашего века благодаря трудам П. Кюри, Дж. Наймана. Ими введено понятие симметрии физических явлений – фундаментальное понятие кристаллофизики. Отцом отечественной кристаллофизики является академик А.В. Шубников (1887-1970). Он ввел понятие о симметрии математических величин и тем самым открыл новый подход к формулированию многих основных законов, устанавливающих связь симметрии кристаллов и явлений. Математический аппарат кристаллофизики – тензорная алгебра. Приведенная на с. 4 схема иллюстрирует классификацию наук, изучающих кристаллы, и место кристаллофизики среди них, на ней отмечены: 1 – кристаллография; 2 – математика; 3 – физика; 4 – химия; 5 – математическая кристаллография; 6 – кристаллофизика; 7 – кристаллохимия; 8 – тензорная алгебра, теория групп; 9 – физика твердого тела; 10 – химия твердого состояния.
 Каждому кристаллическому веществу присущи определенный порядок и симметрия в расположении частиц, четко установившееся расстояние между частицами, причем эти закономерности можно определить качественно и количественно.
Каждому кристаллическому веществу присущи определенный порядок и симметрия в расположении частиц, четко установившееся расстояние между частицами, причем эти закономерности можно определить качественно и количественно.
Расположение частиц в кристалле упорядочено. Под упорядоченным расположением атомов в пространстве понимается свойство пространственной периодичности. Для описания кристаллических форм используются специфические термины.
Структура кристалла – это конкретное расположение частиц в пространстве.
Пространственная решетка – это способ представления периодичности повторения в пространстве отдельных материальных частиц или их групп. Это бесконечное трехмерное периодическое образование, или, точнее, это геометрическое построение, с помощью которого в кристаллическом пространстве выявляются одинаковые точки.
Узлы пространственной решетки – это вершины параллелепипедов, из которых состоит кристаллическая решетка.
Принципиальное различие между структурой кристалла и пространственной решеткой не всегда осознается четко, так как по большей части и ту и другую невольно отождествляют с теми моделями из шариков и проволочек, какими принято иллюстрировать законы расположения частиц в кристаллах.
Нельзя, однако, забывать, что кристаллическая структура – это физическая реальность, а пространственная решетка – лишь геометрическое построение, помогающее выявить законы симметрии или наборы симметричных преобразований кристаллической структуры.
Период решетки. Кратчайшее из возможных расстояний между одинаковыми точками в ряду называется элементарной трансляцией или периодом идентичности или постоянной решетки.
Элементарная ячейка. Это понятие может быть рассмотрено с различных позиций. Если рассматривать кристалл как бесконечную пространственную периодическую совокупность атомов, то в качестве элементарной ячейки может быть выбран параллелепипед, построенный на трех элементарных трансляциях. Объем примитивной элементарной ячейки не зависит от ее формы и является величиной, постоянной для данной решетки; он равен объему, приходящемуся на один узел. Эти параллелепипеды плотно совмещаются друг с другом и заполняют все пространство.
Если же ставить вопрос о возможности исследования закономерностей физических свойств на основе представления об элементарной ячейке, тогда в качестве элементарной ячейки выбирается минимальная совокупность атомов, которая несет информацию о структуре кристалла в целом.
В качестве примера рассмотрим структуру, называемую кубической
гранецентрированной (рис. 1).
 Эта кристаллическая решетка может быть рассмотрена в тетраэдрическом редставлении (рис. 2).
Эта кристаллическая решетка может быть рассмотрена в тетраэдрическом редставлении (рис. 2).
 Если в центр каждого тетраэдра поместить атом того же сорта, что и вся структура, получится решетка типа алмаза. Тетраэдр с атомом в центре называется «алмазным узлом» и может служить примером элементарной ячейки в кристаллографическом рассмотрении, а вся структура (рис. 3) – пример элементарной ячейки в кристаллофизическом плане: это минимальная совокупность атомов, которая несет информацию о физических свойствах и строении всего кристалла в целом.
Если в центр каждого тетраэдра поместить атом того же сорта, что и вся структура, получится решетка типа алмаза. Тетраэдр с атомом в центре называется «алмазным узлом» и может служить примером элементарной ячейки в кристаллографическом рассмотрении, а вся структура (рис. 3) – пример элементарной ячейки в кристаллофизическом плане: это минимальная совокупность атомов, которая несет информацию о физических свойствах и строении всего кристалла в целом.
Если в центр тетраэдров поместить атомы другого сорта, получим решетку типа цинковой обманки.
Структурой алмазного типа обладают: германий, кремний, серое олово, алмаз. Структуру типа цинковой обманки имеют почти все полупроводниковые соединения элементов третьей и пятой групп или элементов шестой и второй групп. Это записывается следующим образом: А3В5 и А2В6.
Структурный тип. Этот термин также заимствован из кристаллографии. Вещества, сходные по своему строению, объединяются в одну совокупность, именуемую структурным типом, и ей присвоено название наиболее известного элемента из этой совокупности. Структурный тип также обозначается буквенно-цифровым символом, например, решетка типа алмаза К4. Буква означает принадлежность кристаллической системе (К – кубическая), а цифра – степень сложности структуры.
Третий способ выбора элементарной ячейки – это построение ячейки Вигнера-Зейтца. Чтобы построить такую ячейку, необходимо выделить какой-либо узел в качестве первоначального, нулевого. Затем к ближайшим узлам провести из нулевого узла векторы. Через середины этих векторов перпендикулярно к ним проводятся плоскости. Совокупность получившихся плоскостей выделяет вблизи выбранного узла некоторую область пространства, которая и называется ячейкой Вигнера-Зейтца. В трехмерном пространстве это многогранник. Как геометрическая фигура, он обладает всеми элементами симметрии решетки по отношению к поворотам и отражениям и содержит один узел в центре ячейки.
Элементарная ячейка – это, по существу, элементарный структурный блок, который, будучи распространенным в направлении декартовых осей многими сдвигами, кратными периоду решетки, образует идеальный трехмерный кристалл.
Выбор ячейки может быть весьма произволен, но наиболее полезен такой выбор ячейки, при котором монокристалл – ячейка содержит все симметрические характеристики кристалла в целом. Известный в кристаллофизике принцип Наймана утверждает, что элементы симметрии любого физического свойства кристалла должны включать элементы симметрии точечной группы кристалла. Так что элементарную ячейку следует выбирать с полезной для физических описаний полнотой симметрических свойств.
Базис решетки. Трехмерные кристаллические решетки обладают дополнительной характеристикой – базисом, т. е. числом атомов, приходящихся на одну элементарную ячейку в пространственной решетке. Для гранецентрированной решетки Fm3m (ГЦК) атомы, находящиеся в вершинах, дают вклад в данную решетку по 1/8, т. е. всего 1/8×8=1 атом, атомы, находящиеся в центрах граней, принадлежат одновременно двум решеткам, т. е. дают вклад по 1/2. Всего таких атомов 6 (6 граней), значит, вклад от них в данную решетку 1/2×6=3. Базис ГЦК структуры равен четырем (рис.4).
Для решетки Jm3m (рис. 5) объемно центрированной (ОЦК) базис находится следующим образом. В решетке восемь атомов в вершинах куба принадлежат одновременно восьми таким же решеткам, так что на долю данной решетки приходится по 1/8 атома, т. е. восемь атомов в данную решетку дают вклад 1/8×8=1. Атом, находящийся в центре, целиком принадлежит данному кубу, так что базис ОЦК решетки равен 2.
Базис задается числом базисных атомов с указанием их координат. Например, для ОЦК 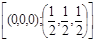 . Базис ГЦК
. Базис ГЦК 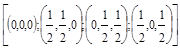 .
.
Элементы симметрии
Кристаллических структур
Симметричной фигурой называется фигура, которая может совместиться сама с собой в результате симметричных преобразований. Русский кристаллограф… Отражения и вращения, приводящие геометрическую фигуру в совмещение с самой… Воображаемые плоскости, линии и точки, с помощью которых осуществляются эти отражения и вращения, называются…Поворотная ось или ось симметрии
. При использовании интернациональной символики порядок оси обозначается «n» или… Преобразования пространственной симметрии, производимые над кристаллом любой структуры, относятся, в конечном счете, к…Плоскость зеркального отражения
Матрица представления для плоскостей зеркального отражения не может быть записана в общем виде, для каждой плоскости отдельно она имеет свой вид.…Центр симметрии
Обозначение в интернациональной системе , по Шенфлису – Сi. Матрица представления центра симметрииСоставные элементы симметрии
Операция симметрии представляет последовательное применение операции поворота плюс операцию зеркального отражения. Матрица представления – это… 2. Инверсионная ось. Инверсионная ось симметрии – ; действие ее включает в… Все рассмотренные элементы симметрии: ось симметрии, зеркально-поворотная ось, плоскость зеркального отражения, центр…Таблица 1
| Обозначение элемента симметрии или сочетания | Расшифровка | Дополнительные сведения |
| Х, Сn | Поворотная ось | 
|
| m, sn, sv | Плоскость симметрии |  , m ^оси Z , m ^оси Z
|
Окончание табл. 1
| Обозначение элемента симметрии или сочетания | Расшифровка | Дополнительные сведения |
 , Сi , Сi
| Центр симметрии или инверсии | 
|

| Зеркально-поворотная ось | 
|
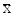
| Инверсионная ось | 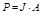
|
| Хm | Ось симметрии и параллельная ей плоскость симметрии | |

| Ось симметрии и перпендикулярная ей плоскость симметрии | |
| Х2 | Ось симметрии второго порядка, перпендикулярная оси симметрии Х-го порядка | |
| 2Х | Присутствие осей симметрии Х и второго порядка |
Рассмотрим такие сочетания элементов симметрии, как 23 и 32. В записи встречаем присутствие осей симметрии второго и третьего порядков, но во втором случае эти оси взаимно перпендикулярны. На рис. 12 показан характер расположения осей и соответственно различный вид многогранников, соответствующих каждому из этих сочетаний.
 Рис. 12. Пример различных комбинаций осей 32 и 23
Рис. 12. Пример различных комбинаций осей 32 и 23
Определим симметрию гранецентрированной решетки Fm3m.
4С3 – четыре оси симметрии третьего порядка;
6m – 6 плоскостей симметрии, параллельных этим осям;
6С2 – 6 осей симметрии 2 порядка;
3С4 – 3 оси симметрии 4 порядка;
3m – 3 плоскости симметрии, перпендикулярные этим осям;
J – центр симметрии.
Симметрия решетки типа ZnS-F 3m: 4С3, 6m, 3С4, 6С2.
3m: 4С3, 6m, 3С4, 6С2.
Трансляционная симметрия
, n1, n2, n3 – целые числа. – вектор трансляции. Операцию перемещения кристалла как целого параллельно самому себе, описываемую вектором , называем трансляцией. Вектор…Решетки и трансляционная симметрия
Решетка отображает симметрию структуры независимо, совпадает ли узел с атомом того или иного типа или с промежутком между атомами. Структура кристалла – это конкретное расположение частиц в пространстве,… Пространственная решетка характеризует периодичность повторения в пространстве отдельных материальных частиц.Элементы теории групп
Рис. 13. Совокупности точек, связанных различными операциями симметрии 1. Точечная группа не содержит элементов симметрии и обозначается –1.Свойства операций симметрии
1. Если кристаллическая структура характеризуется определенным набором элементов симметрии, то результатом следующих одно за другим преобразований… Пусть S и R – операции симметрии. Подействовав на функцию сначала оператором , получим тождественное (симметричное) состояние, т. е.Элементы симметрии пространственных групп
. Для каждой структуры характерен набор ее элементарных трансляций или… Пространственная группа кристалла включает в себя плоскости симметрии, простые и инверсионные оси 1, 2, 3, 4, 6…Решетки Бравэ
Исходя из идеи о периодическом расположении центров сферических материальных частиц в кристаллическом веществе, О. Бравэ в 1848 году показал, что…Таблица 2
| Кристаллическая система | Число ячеек | Симметрия ячеек | Характеристики элементарной ячейки |
| Триклинная | P | a¹b¹c a¹b¹g | |
| Моноклинная | P,C | a¹b¹c a=b=900¹g | |
| Ромбическая | P,C,J,F | a¹b¹c a=b=g=900 | |
| Тетрагональная | P,J | a=b¹c a=b=g=900 | |
| Кубическая | P,J,F | a=b=c a=b=g=900 | |
| Ромбоэдрическая | R | a=b=c 900¹a=b=g<1200 | |
| Гексагональная | P | a=b¹c a=b=900 g=1200 |
 Каждая решетка Бравэ – это группа трансляций, характеризующих расположение материальных частиц в пространстве.
Каждая решетка Бравэ – это группа трансляций, характеризующих расположение материальных частиц в пространстве.
Решетки Бравэ играют исключительно важную роль в кристаллографии. Любую кристаллическую структуру можно представить с помощью одной из 14 решеток Бравэ. Обозначение соответствующих осей и углов приведено на рис. 15.
Для выбора ячейки Бравэ используют три условия:
1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла, точнее наиболее высокой симметрии той сингонии, к которой относится кристалл. Ребра элементарной ячейки должны быть трансляциями решетки.
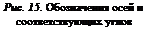 2. Элементарная ячейка должна содержать максимальное число прямых углов и равных углов и равных ребер.
2. Элементарная ячейка должна содержать максимальное число прямых углов и равных углов и равных ребер.
3. Элементарная ячейка должна иметь минимальный объем.
Типов решеток Бравэ
– примитивные (Р); – базоцентрированные (С); – объемно центрированные (J);Индексы узлов
, , , где a, b, c – параметры решетки; u, v, w – целые числа. Если за единицу измерения длин вдоль осей решетки принять параметры самой решетки a, b, c, то координатами узла будут…Индексы направления
Совокупность направлений, которые могут симметрично совместиться друг с другом с помощью преобразований симметрии, свойственных одному классу… Индексы направления представляют собой три наименьших целых числа,… Оси координат в кубической решетке имеют символы: Ох – [100], Оy- [010], Оz – [001]. Все параллельные направления в…Символы плоскостей
Пусть какая-либо плоскость решетки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc (m, n, p – целые числа). Отношение чисел… Серию отношений рациональных чисел m:n:p для всех параллельных плоскостей…Таблица 4
| Номер плоскости | Отрезки по осям | m:n:p | ||
| x | y | z | ||

| 2: :1 = 4:1:2 :1 = 4:1:2
| |||
| 4:1:2 | ||||
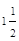
| 6: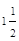 :3 = 4:1:2 :3 = 4:1:2
| |||
| 8:2:4 = 4:1:2 |
В кристаллографии и кристаллофизике принято характеризовать плоскости (или направления к ним) не параметрами, а индексами Миллера.
Индексы Миллера – это величины, обратные параметрам Вейсса, приведенные к целым числам. Если параметры плоскости p,q,r, то индексы Миллера определяются из соотношения
 :
: :
: = h:k:l.
= h:k:l.
Числа h, k, l, не имеющие общего множителя, носят название индексов Миллера плоскости. Индексы, написанные подряд, без запятых, и заключенные в круглые скобки – (hkl), называют символом плоскости. Символом (hkl) характеризуется весь набор параллельных плоскостей. Набор физически эквивалентных плоскостей представлен символом {hkl}. В этом символе в фигурных скобках заключена вся совокупность физически эквивалентных плоскостей, которая может быть получена путем перестановки индексов, смены знаков индексов.
Если плоскость параллельна какой-либо оси координат, т. е. пересекается с этой осью в бесконечности, то индекс этой плоскости по этой оси будет  .
.
Символы координатных плоскостей независимо от углов между осями всегда будут XOY = (001), XOZ = (010), YOZ = (100).
Метод описания граней и ребер кристалла с помощью индексов и символов установили задолго до того, как на опыте была доказана решетчатая структура кристалла. Он основывался на замечательном эмпирическом законе кристаллографии - законе целых чисел или законе рациональных отношений.
Этот закон утверждает: для любых двух граней реального кристалла двойные отношения параметров равны отношению целых чисел. Плоскость может быть гранью кристалла, только в том случае, если отрезки, отсекаемые ею на осях координат, и «единичные» отрезки связаны между собой соотношением
 :
: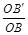 :
: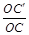 = p:q:r,
= p:q:r,
где p, q, r – целые, взаимно простые и для реальных кристаллов малые числа (рис. 20).
Именно поэтому на растущем кристалле появляются только грани определенного наклона, характерного для данного вещества.
 Грани, для которых отношение p:q:r является иррациональным, невозможны в реальном кристалле, как правило, p, q, r – числа, не превышающие пяти. Если эти числа будут целые, но больше 5, то грань возможна, но ее появление маловероятно.
Грани, для которых отношение p:q:r является иррациональным, невозможны в реальном кристалле, как правило, p, q, r – числа, не превышающие пяти. Если эти числа будут целые, но больше 5, то грань возможна, но ее появление маловероятно.
Итак, любую кристаллографическую плоскость и любую грань кристалла можно определить тремя целыми числами – индексами Миллера, которые обладают следующими свойствами:
1) это целые не имеющие общего множителя числа;
2) они обратно пропорциональны отрезкам, отсекаемым плоскостью от начала координат;
3) все параллельные плоскости обозначаются одним набором индексов Миллера;
4) если плоскость параллельна какой-либо оси, соответствующий индекс равен нулю;
5) в кристаллах кубической системы плоскость и нормаль к ней обозначаются одинаковым набором индексов Миллера.
Чтобы найти индексы Миллера любой кристаллографической плоскости, надо прежде всего выбрать начало координат (но не в данной плоскости); затем выразить отрезки, отсекаемые плоскостью на
оси координат, через осевые отрезки а, b, с, далее найти обратные значения этих величин, привести их к виду наименьших возможных рациональных дробей, имеющих общий знаменатель, и заключить
по лученные числа в круглые скобки (рис. 21).
лученные числа в круглые скобки (рис. 21).
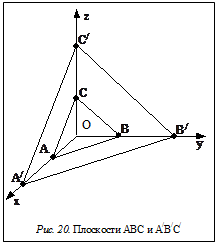
Рис. 21. Основные направления и плоскости куба:
а – индексы осей симметрии, диагоналей граней и пространственных диагоналей
кубической решетки; б – индексы основных плоскостей кубической решетки
Рассмотрим ряд примеров
Пример 1
Определить индексы плоскости, отсекающей на осях решетки отрезки А = 1, В = 2,С = 4.
Отношения  :
: :
: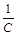 =
=  :
: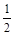 :
: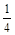 представляют рациональные числа. Общим знаменателем правой части является 4. Множителями являются 4 и 2. Поэтому h = 4, k = 2, l = 1 (421).
представляют рациональные числа. Общим знаменателем правой части является 4. Множителями являются 4 и 2. Поэтому h = 4, k = 2, l = 1 (421).
Пример 2
Определить индексы плоскости, отсекающей на осях решетки отрезки А = 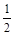 , В = 2 и С =
, В = 2 и С = 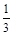 . Отношения
. Отношения  :
: :
: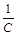 =
= :
: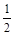 :
: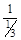 - тоже рациональные числа. Общим знаменателем является 2.
- тоже рациональные числа. Общим знаменателем является 2. 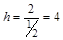 ,
, 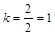 ,
, . Это и есть индексы плоскости (416).
. Это и есть индексы плоскости (416).
Отрезки, отсекаемые плоскостью на осях решетки, следующим образом выражаются через индексы этой плоскости: они обратно пропорциональны индексам плоскостей.
Пример 3
Определить отрезки, которые отсекает на осях решетки плоскость (123). Записываем величины, обратные индексам плоскости:  . Общий знаменатель равен 6, поэтому отрезки, отсекаемые плоскостью от осей, будут равны 6, 3, 2.
. Общий знаменатель равен 6, поэтому отрезки, отсекаемые плоскостью от осей, будут равны 6, 3, 2.
Основные геометрические соотношения в кристаллах
Уравнение, связывающее индексы плоскости и прямой hu + kv + + lw = 0, называется уравнением закона зон. Если индексы (hkl) заданы, то подбором всех u, v, w, удовлетворяющих данному… 2. Если две прямые лежат в плоскости или параллельны ей, то, зная их индексы, можно определить индексы плоскости.Гексагональных кристаллов
Плоскости с первой по шестую (на рисунке изображены проекции граней на ось XOY) являются физически эквивалентными плоскостями, плоскости с 7 по 9… Обозначим все плоскости с помощью индексов Миллера: 1. ()Правила работы с сеткой Вульфа
1) Приготовить наклеенную на картон сетку Вульфа, кальку, карандаш.
2) Сетку располагают так, чтобы ее экватор был горизонтален. На сетку кладут кальку, отмечается центр проекции, и на правом конце экватора отмечают нулевую точку. По этим меткам всегда можно привести чертеж в исходное положение.
3) Вся работа проводится на кальке, никакие отметки на самой сетке не допускаются.
4) Все построения проводятся путем вращения кальки относительно сетки.
Примеры решения задач с помощью сетки Вульфа
Задача 1. Построить стереографическую проекцию точки с заданными координатами r и j.
Решение
2) Отсчитываем заданный угол от jо по основному кругу проекции по часовой стрелке и отмечаем точку на круге. 3) Поворачиваем кальку так, чтобы найденная точка попала на конец одного из… 4) По данному диаметру отсчитываем r, ведя отсчет от центра сетки (rо = 0). Для углов 0о £ r £ 90о…Решение
2) Делаем отметку на конце диаметра сетки, по которому отсчитываем r. 3) Возвращаем кальку в прежнее положение и от этой отметки отсчитываем j по… Задача 3. Измерить угол между направлениями. Стереографическая проекция направления – есть точка. Угол между…Решение
Вращая кальку, приводим обе точки на один меридиан. Этот меридиан и является стереографической проекцией искомой плоскости.
Задача 5. По полюсу построить плоскость (полюсом называется стереографическая проекция нормали к плоскости).
Решение
1) Вращая кальку, выводим полюс на экватор сетки.
2) Отсчитываем по экватору 900 в направлении центра сетки и отмечаем меридиан, проходящий через точку отсчета. Этот меридиан и является искомым.
Задача 6. Найти полюс плоскости.
Решение
1) Стереографическая проекция плоскости – есть дуга. Вращением кальки добиваемся совмещения дуги с одним из меридианов.
2) Отсчитываем 900 от точки пересечения дуги с экватором в сторону центра проекции. Найденная точка отсчета и есть полюс плоскости.
Задача 7. Найти индексы плоскости (h1 h2 h3), если задана проекция его полюса.
Решение
Очевидно, что (суммирование по повторяющемуся индексу в правой части формулы не проводить); gi – углы между нормалью к плоскости и соответствующей… Рис. 28. Иллюстрация к задаче 7Построение стереографической проекции