Движение тел переменной массы. Реактивное движение

До сих пор мы считали, что масса тел в процессе их движения не меняется. Но так обстоит дело не всегда.

Рассмотрим, например, движение ракеты — классический пример тела, масса которого уменьшается по мере расхода топлива (рис. 4.4).

Рис. 4.4

Пусть в момент времени t масса ракеты m, а её скорость 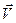. Спустя dt секунд скорость ракеты увеличится на , а масса уменьшится на величину dm и станет (m – dm).

dm — масса сгоревшего топлива, которое покинуло ракету со скоростью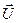относительно неё. Изменение импульса системы за время dt можно представить в следующем виде:

.

Слагаемым dm∙dV пренебрежем как малой величиной высшего порядка по сравнению с остальными слагаемыми. Значит

.

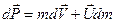Это изменение импульса системы равняется импульсу действующей внешней силы

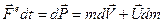
Полученный результат перепишем в форме уравнения движения

(4.14)

Здесь: слева — произведение массы ракеты на её ускорение,

справа — действующие силы: — внешняя сила,

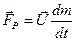— реактивная сила.

Реактивная сила возникает потому, что вылетающим продуктам сгорания сообщается относительная скорость 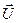. Вначале топливо было в покое относительно ракеты. Затем оно двигалось ускоренно и достигло скорости 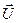. Это ускорение обусловлено силой взаимодействия продуктов сгорания с ракетой. Но по третьему закону Ньютона сила действует не только на продукты сгорания, но и на ракету. Это и есть реактивная сила, пропорциональная относительной скорости 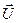и секундному расходу топлива .

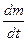Уравнение (4.14) называется уравнением движением тела переменной массы. Оно было впервые получено И.В. Мещереным и носит его имя:

(4.15)

где: — реактивная сила.

Теперь посмотрим, как будет двигаться ракета, на которую не действуют никакие внешние силы (= 0). Движение ракеты будем считать прямолинейным и спроецируем уравнение (4.15) на направление её движения:

;

отсюда:

;

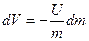или

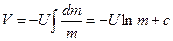. (4.16)

Постоянную интегрирования с найдём из начального условия. Будем считать, что в начальный момент полета — в момент старта — скорость ракеты V₍₀₎ = 0, а её масса равна стартовому значению m₀.

Перепишем (4.16) для этих начальных условий:

V₍₀₎ = 0 = —U∙ln∙m₀ + c,

то есть

c = U∙ln∙m₀

Используя этот результат в уравнении (4.16) получим

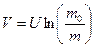. (4.17)

Это соотношение называется формулой Циолковского.

Используя эту формулу, оценим, например, какой должна быть стартовая масса ракеты m₀, чтобы вывести на околоземную орбиту груз массой m = 10³ кг.

Первая космическая скорость составляет V = 8 км/с, а относительная скорость истечения продуктов сгорания U — порядка 2 км/с.

Тогда

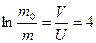
и

кг.

Если скорость истечения U принять равной 1 км/с, то есть вдвое меньше, то стартовая масса ракеты возрастёт до значения 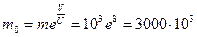кг.

То есть 3 тысячи тонн!

Таково влияние качества ракетного топлива на стартовую массу ракеты.

Лекция 5 «Динамика материальной точки»

План лекции

1. Движение в неинерциальных системах отсчёта. Силы инерции.

1.1. Силы инерции, возникающие при ускоренном поступательном движении системы отсчёта.

1.2. Сила инерции, действующая на тело, неподвижное во вращающейся системе отсчёта.

1.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчёта.

1. Движение в неинерциальных системах отсчёта

Законы Ньютона — основа классической механики — справедливы лишь в инерциальных системах отсчета.

Опытным путем можно установить инерциальность или неинерциальность той или иной конкретной системы.

Но если инерциальность одной системы отсчёта установлена, то, воспользовавшись принципом относительности Галилея, можно создать сколько угодно инерциальных систем. Ведь любая система, движущаяся относительно инерциальной прямолинейно, поступательно и равномерно, тоже является инерциальной.

Отсюда легко сделать вывод, что ускоренно движущаяся или вращающаяся система отсчёта — неинерциальная.

Как в такой — неинерциальной — системе описать движение тела?

В качестве уравнения движения в неинерциальной системе отсчёта вновь используется уравнение второго закона Ньютона. Но наряду с привычными, знакомыми нам силами, здесь приходиться привлекать совсем новые, необычные силы, которые получили название «силы инерции».

Познакомимся с этими силами, рассматривая движение тела в разных неинерциальных системах отсчёта.

1.1. Силы инерции, возникающие при ускоренном поступательном движении системы отсчёта

Это классическая задача о поведении маятника, прикреплённого к потолку железнодорожного вагона (рис. 5.1). Вагон движется ускоренно. Его ускорение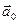

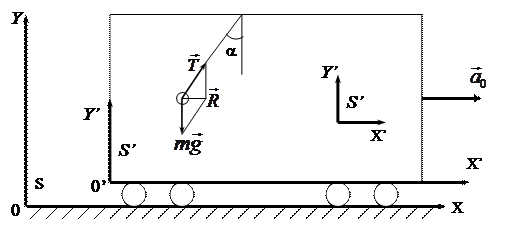
Рис. 5.1

Маятник, конечно, примет положение, изображённое на рисунке.

При этом на отклонившейся грузик маятника действуют две силы: гравитационная (сила тяжести) 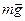и упругая (сила натяжения нити) 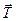. Равнодействующая этих двух сил и определит ускорение маятника 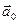. Ведь маятник движется вместе с вагоном с ускорением :

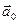R = mg × tga = ma₀

Это и есть уравнение движения грузика m, записанное в неподвижной системе отсчёта S, связанной с Землёй.

Теперь рассмотрим это же движение, перейдя в движущийся вагон.

В системе отсчета S’, связанной с вагоном, мы обнаружим необычную картину: маятник отклонился на угол a и застыл неподвижно, хотя на него действует сила

R = mg × tga = ma₀!

Налицо нарушение всех законов механики: на тело действует сила, а оно остаётся при этом в покое. Создается впечатление, что на шарик действует ещё одна сила 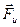, равная , но противоположного направления (рис. 5.2).

Рис. 5.2

Приложим эту силу, и всё становиться на свои места: равнодействующая сил, действующих на тело, равна теперь нулю и тело остаётся в покое. Его скорость V’ и, главное, ускорение a’ относительно вагона (в системе S’) равны нулю.

.

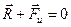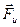— сила инерции, возникшая в результате ускоренного движения системы отсчёта

. (5.1)

Она равна произведению массы тела на ускорение системы отсчёта 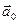. Но направлена сила инерции 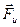в сторону, противоположную .

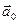Иногда эту силу называют фиктивной силой инерции, имея в виду её особые свойства. Представим, что при резком торможении вагона, чемодан падает с полки, то есть начинает двигаться ускоренно относительно вагона. Но при этом вы не сможете указать предмет, который подействовал на чемодан и заставил его двигаться с ускорением. У фиктивной силы инерции — силы действия — нет силы противодействия.

1.2. Сила инерции, действующая на тело, неподвижное во вращающейся системе отсчёта

Перенесём наш маятник на диск, вращающийся с угловой скоростью w вокруг вертикальной оси (рис. 5.3).

 

Рис. 5.3

Маятник отклонится от вертикали, двигаясь по окружности радиуса r.

Движение происходит под действием сил тяжести 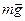и натяжения нити 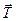. Их равнодействующая , направленная по радиусу к центру окружности, обеспечивает центростремительное ускорение .

Легко записать уравнение движения грузика m в неподвижной, инерциальной системе отсчёта S

R = mg ×tga = mw²r. (5.2)

Теперь перейдём на вращающийся диск и посмотрим на движение маятника в системе отсчёта, вращающейся вместе с диском S’ (рис. 5.4). Мы вновь увидим необычайную картину:

Рис. 5.4

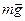в этой системе отсчёта маятник неподвижен. Но на него, несомненно, действует сила , представляющая собой равнодействующую двух сил и 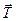. Во вращающейся, неинерциальной системе отсчёта тело, вопреки второму закону Ньютона, остаётся в покое, несмотря на действие вполне реальной силы . Можно воспользоваться уравнением движения Ньютона и в этом случае, если добавить к системе реально действующих сил ещё одну — силу инерции 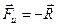(рис. 5.4). Теперь равнодействующая всех сил, действующих на тело (вместе с силой инерции) равна нулю. Поэтому тело остаётся в покое и его ускорение тоже равно нулю.

.

Или

. (5.3)

Во вращающейся системе отсчёта грузик маятника оказался в покое в результате действия трёх сил: силы тяжести 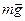, упругой силы натяжения нити 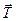и силы инерции .

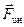Сила инерции в данном случае называется центробежной.

Центробежная сила равна центростремительной, но направлена по радиусу не к центру вращения, а в противоположную сторону — от центра.

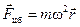(5.4)

Отметим, что центробежная сила инерции, действующая на тело, неподвижное во вращающейся системе отсчёта, зависит от положения этого тела. С увеличением расстояния до оси z, растёт и центробежная сила инерции F_цб. Это особенно хорошо видно, если разместить на вращающемся диске несколько маятников на разных расстояниях от оси вращения (рис. 5.5)

Z

Рис. 5.5

1.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчёта.

Рассмотрим самый простой случай: шарик массой т равномерно движется со скоростью v₀ вдоль радиуса вращающегося диска. Чтобы обеспечить такое движение снабдим шарик направляющим стержнем, по которому он мог бы перемещаться без трения. Нитка, прикрепленная к шарику, позволит ему в радиальном направлении двигаться с постоянной скоростью v₀ (рис. 5.6).

 

Рис. 5.6

Диск вращается с угловой скоростью w. Опишем движение шарика в неподвижной инерциальной системе отсчёта S(x, y). В этой системе движение шарика складывается из двух движений: равномерного прямолинейного — по радиусу диска со скоростью v₀ и кругового движения с угловой скоростью w.

В результате сложения этих двух движений, шарик будет двигаться по криволинейной траектории — разворачивающейся спирали.

В произвольный момент времени t шарик на расстоянии r от оси вращения будет иметь радиальную скорость v₀ и касательную — тангенциальную скорость, связанную с вращением диска (wr) (рис. 5.7).

Рис. 5.7

Посмотрим, как изменятся эти скорости шарика спустя малое время dt.

Во-первых, вся картина скоростей повернётся на угол da = wdt (рис. 5.7 б). Во вторых, радиальная скорость (оставаясь неизменной по величине — V₀) получит приращение:

dV₁ = V₀da = V₀wdt, (5.5)

связанное с повтором вектора скорости V₀ на угол da = wdt.

Изменится и тангенциальная скорость. Её изменение по величине определяется тем, что шарик удалится от оси вращения на расстояние dr = V₀dt. Поэтому:

dV₂ = w(r + dr) – wr = wdr = wV₀dt. (5.6)

Кроме того, эта скорость изменится на величину:

dV₃ = wrda = wrwdt = w²rdt, (5.7)

в связи с поворотом вектора этой скорости на угол da.

Проанализировав все эти изменения, придём к выводу, что в радиальном направлении изменение скорости составит величину:

dV_r = dV₃ = w²rdt,

а в тангенциальном:

dV_t = dV₁ + dV₂ = 2wV₀dt.

Разделив эти изменения на промежуток времени dt, получим соответствующие компоненты ускорения:

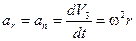; (5.8)

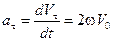. (5.9)

Несложно ответить на вопрос: какие силы обеспечивают эти ускорения?

Центростремительное ускорение создаётся упругой силой натяжения нити (F_ц.с. = F_упр. = ma_ц.с. = mw²r), направленной по радиусу к оси вращения. Касательное ускорение a_t поддерживается упругой силой деформированного стержня (= ma_t = m2wV₀). Стержень при движении прогибается и действует на шарик с силой, направленной в сторону вращения (рис. 5.8).

 

 

 

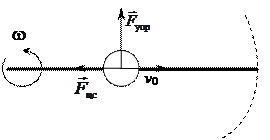
Рис. 5.8

Запишем уравнения движения шарика в инерциальной системе отсчёта. Это уравнения второго закона Ньютона для двух движений — вдоль радиуса:

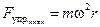, (5.10)

и в перпендикулярном направлении:

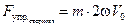. (5.11)

Теперь посмотрим, как представляется движение этого же шарика наблюдателю, вращающемуся вместе с диском.

Этот наблюдатель видит, что шарик в его вращающейся системе отсчёта движется равномерно и прямолинейно со скоростью 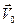= сonst вдоль радиуса диска. Ускорение шарика равно нулю, но при этом на него действует упругая сила натяжения нити F_ц.с. = mw²r и упругая сила деформированного стержня F = m2wV₀. Их равнодействующая никак не может быть равна нулю.

Для того, чтобы записать уравнение движения этого тела в неинерциальной системе отсчёта в виде уравнений второго закона Ньютона, к реально действующим упругим силам прибавим две силы инерции (рис. 5.9):

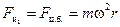(5.12)

и

. (5.13)

 

 

Рис. 5.9

Теперь и в радиальном и в тангенциальном направлениях суммы сил будут равны нулю, что и объясняет равномерное движение шарика вдоль радиуса.

С первой из сил инерции 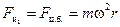мы знакомы. Это центробежная сила инерции.

Вторая сила инерции называется силой Кориолиса.

Эти силы можно записать в векторном виде:

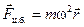
и

.

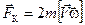Подводя итог рассмотрению движений в неинерциальных системах отсчёта, отметим следующие основные моменты.

Ньютоновским уравнением движения можно воспользоваться и в неинерциальных системах отсчёта. Но при этом систему реально действующих сил нужно дополнить силами инерции.

В неинерциальной системе отсчёта, движущейся прямолинейно и поступательно с ускорением 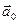, сила инерции равна:

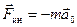. (5.14)

В неинерциальной системе отсчёта, вращающейся с угловой скоростью w, в общем случае следует ввести две силы инерции:

центробежную 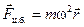, (5.15)

и кориолисову 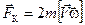. (5.16)

Лекция 6 «Работа и энергия»

План лекции

1. Работа и кинетическая энергия. Теорема о кинетической энергии. Теорема Кёнига.

2. Консервативные и неконсервативные силы.

3. Потенциальная энергия.