Огляд деяких систем числення

Сам процес числення (нумерація) - сукупність певних прийомів (правил, алгоритмів) представлення натуральних чисел. Систем числення існує багато.

У будь-якій системі числення прийняті деякі символи (знаки, слова) для позначення певних чисел, ці знаки називають базовими (вузловими). Наприклад, в 10-ій системі базовими є знаки (зображення) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, що позначають цілі натуральні числа від 0 до 9 і дроби за допомогою коми (крапки).

Решта чисел уявного діапазону числової вісі мають назву алгоритмічні і створюються в результаті виконання дій за певними правилами над базовими числами (10, 123, 543). Тому системи числення відрізняються одна від одної вибором базових (вузлових) чисел і способами утворення алгоритмічних. При письмовому позначенні вони відрізняються характером використаних числових знаків і принципами їх запису. Наприклад, у стародавніх вавілонян базовими були числа 1,10,60; у племені маорі (Нова Зеландія) - 1, 11, 112, 113; у римській системі числення вузловими були числа 1, 5, 10, 50, 100, 500, 1000, які позначалися знаками І, V, X, L, C, D, M: приклад MCMXCVII - 1997.

Системи числення, в яких алгоритмічні числа утворюються складанням вузлових, називаються адитивними. Наприклад, в стародавньоєгипетській системі числення числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 19, 40 позначалися відповідно:

 

У римській системі числення числа виходять шляхом складання і віднімання вузлових.

У сучасних числах (в т.ч. європейських, українській і російській мовах, ін.) застосований адитивно-мультиплікативний спосіб. В деяких країнах були прийняті алфавітні системи числення - наприклад, греки, стародавні слов’яни, ін. (цифри від 1 до 9 зображалися буквами алфавіту з межею зверху).

Будь-яка призначена для практичних розрахунків система числення повинна забезпечувати:

- однозначність відображення числа;

- представлення всіх чисел в діапазоні числової осі;

- простоту запису чисел і виконуваних операцій над ними;

- систему правил запису і читання чисел.

Системи числення діляться на позиційні і непозиційні.

Позиційна система числення - система, в якій значення базових знаків залежить від їх місцеположення в числі, розрядності.(Тобто 0…9 в розряді одиниць не дорівнює 0…9 в розряді десятків, сотень, тисяч, ін. - бо прийнято, що вага сусідніх розрядів таких чисел різниться на порядок).

Непозиційна система числення- система, в якій значення базових знаків не залежить від їх місцеположення в числі, розрядності.

Принцип побудови таких систем полягає у виборі базових знаків і при читанні (або запису) проводяться операції складання (іноді і віднімання). Наприклад: Робінзон Крузо застосував непозиційну систему числення для підраховування діб. Базовий знак - вертикальна риска, які він складав і отримував числа. Ця система неефективна з двох причин:

- запис числа може виявитися довгим і незручним;

- для виконання підрахунків необхідно використовувати іншу систему.

Проте вона дуже проста.

Римську систему числення можна назвати частково позиційною, хоча вона вважається непозиційною системою. Так, наприклад, в числах LX і XL знак X (10) приймає два значення ±10 і залежить від свого місцеположення відносно L (справа чи зліва).

 

2.2 Система залишкових класів

Однією з непозиційних систем числення, розробленою спеціально для застосування в спеціалізованих ЕОМ, є система в залишкових класах (СЗК).

Ідейне коріння СЗК пов’язане з працями Ейлера, Гауса і Чебишева з теорії порівнянь. Значний внесок в розвиток СЗК внесли чеські вчені математики М. Валах і А. Свобода, що працювали над представленням чисел у вигляді сукупності ненегативних вирахувань по групі взаємнопростих основ [1-21].

Хай необхідно записати число N, задане в 10-ій системі в системі СЗК.

Кінцеву множину позитивних цілих чисел, взаємно простих між со-бою, назвемо базисом основ системи числення в залишкових класах [14] .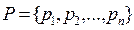

Під системою числення в залишкових класах будемо розуміти таку систему, в якій ціле число представляється у вигляді набору залишків (вирахувань) по вибраних основах р_i.

Тоді число N в СЗК буде записано як: 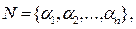(2.1)

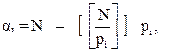де (2.2)

тобто a_i – є відображення числа N у вигляді позитивного залишку від ділення N націло на основу Р_i.

При цьому буде завжди справедлива нерівність a_i<p_i. (де і=1,2…n).

У відомій з теорії чисел першій і другій функціональній теоремі Гауса, доведено, що якщо числа р_i взаємно прості між собою, то опис {a₁, a₂, a_n}, що представляє N, є єдиним.

Нагадаємо, що взаємно простими числами називають числа, що мають найменший загальний дільник (НЗД), що дорівнює 1. Наприклад, 15 і 22 є взаємно прості числа (оскільки НЗД рівний 1).

Приклад. Нехай вибрані основи СЗК: р={3,5,7}. Представимо десяткове число N=67 у СЗК.

Рішення. Знайдемо залишки згідно виразу 2.2

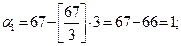
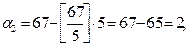
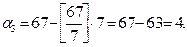
Отже, число 67 записується в СЗК як {1,2,4}, або в двійковій - {001,010,100}.

Діапазон чисел, що представляються, дорівнює: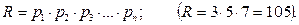

Зворотний переклад числа з СЗК в десяткову систему проводиться за формулою:

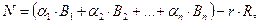(2.3)

де r - ранг, що приймає значення 0, 1, 2, … так, щоб права частина виразу 2.3 була менше R;

B_i - ортогональний базис, що визначає при виборі базису СЗК.

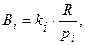
де k_i - ціле позитивне число (k_i=1, 2, …, р_і-1), при цьому k_i вибирається таким, щоб залишок від ділення В_і на р_і дорівнював одиниці (тобто вага базису k_i вибирається виходячи з рівності):

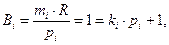(2.4)

Приклад. Визначимо для СЗК з основами {3,5,7} ортогональні базиси B_i та переведемо число {1,2,4} в десяткову систему.

;

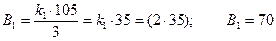(для р₁=3 умова 2.4 виконується при k=2),

;

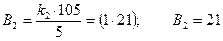(для р₂ =5 умова 2.4 виконується при k=1),

;

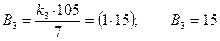(для р₃ =7 умова 2.4 виконується при k=1), тоді N = (a₁×B₁+a₂×B₂+a₃×B₃) - r × R = (1×70+2×21+4×15) - r ×105 =172-1×105=67.

Запишемо число 67 в двійковій системі 1000011 і в СЗК 001_ 010_ 100. Цифри СЗК в кожному розряді вирахувань по-перше, незалежні один від одного і не залежать від позиції, а лише залежать від базису; по-друге, кожен розряд вирахувань несе інформацію про число в цілому. Ця властивість СЗК використовується для відновлення спотвореної інформації при передачі по лінії зв’язку.

 

3 ПОЗИЦІЙНІ СИСТЕМИ ЧИСЛЕННЯ

 

3.1 Представлення чисел в позиційних системах числення

Система числення, в якій значення базисної цифри визначається її положенням в розрядах числа, називається позиційною. Наприклад, в десятковій системі числення в числі 222, перша цифра зліва від коми означає дві одиниці, друга - два десятки, третя - дві сотні.

Позиційна система числення визначається своєю основою.

Основа q позиційної системи числення - кількість знаків, що використовуються для відображення числа в даній системі.

Якщо q - ціле позитивне число, то позиційна система числення називається природна.

Позиційних систем числення може бути багато оскільки за основу можна прийняти будь-яке число і утворити нову систему числення.

Число в позиційній системі числення визначається рівністю:

,

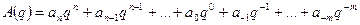або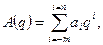

де а_i - коефіцієнти розрядів в знаках системи; q - основа системи числення; A(q) - довільне число; m, n - кількість дробових і цілих розрядів.

При записі числа, запис основи і знак "+" опускають, а ступінь визначають по розряду від коми,

тобто .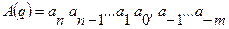

Наприклад, число 934,125 записано в десятковій системі числення. Число 124,57₍₈₎ записано у 8-й системі числення (беруться цифри 0, 1, ..., 7).

У двійковій системі числення використовують цифри 0, 1.

Наприклад, число 1001,1 = 1×2³ + 1×2⁰+1×2^-1 =17,5 (див. таблицю 3.1).

Вага розряду Р_i числа в позиційній системі числення- це відношення 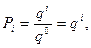де і - це номер розряду справа наліво. Вага розрядів росте справа наліво. Якщо візьмемо розряд Р_і=10^К, то наступний старший матиме вагу P_i+1=10^K+1, а молодший P_i-1=10^K-1. Такий взаємозв’язок розрядів припускає, при виконанні операцій, передачу інформації між ними.

Таблиця 3.1 - Еквіваленти десяткових чисел в різних системах числення

	Десяткова цифра
	q=2	q=3	q=5	q=8	q=16
					A
					В
					С
					D
					E
					F

 

Якщо в даному розряді накопичилося значення одиниць (десятків, сотень, і т.д.) рівне або більше q, то повинна відбуватися передача одиниці в сусідній, старший розряд. При складанні, такі передачі назвемо переносом одиниці в старший розряд, а при відніманні – позикою одиниці із старшого розряду. Приклад: 9 + 2 = 11; 17 – 8 = 9.

Глибина числа– це кількість знаків (зображень), які використано при записі числа в одному розряді. Поняття «глибина числа» співпадає з поняттям «основа» і дорівнює значенню q – тобто для 10-ї, 8-ї, 2-ї систем числення, відповідно: 0, 1, 2, …, 9 (десять); 0, 1, 2, …, 7 (вісім); 0, 1 (два).

Довжина числа– це кількість розрядів в записі числа. Часто вжива-ється термін – довжина розрядної сітки пристрою (кількість розрядів n).

Для різних систем характерна своя довжина розрядної сітки для запису одного і того ж числа. Наприклад, 96₍₁₀₎ = 140₍₈₎ = 10120₍₃₎ = 1100000_(2). Чим менша основа, тим більше потрібно розрядів для запису числа і навпаки.

 

 

Рисунок 3.1 Числова вісь діапазону чисел, що представляються

Величина розрядної сітки n, що прийнята в ЦА, у свою чергу накладає обмеження на уявний діапазон чисел (яким він може оперувати) – це інтервал числової вісі між максимальним і мінімальним числом (рис. 3.1). У загальному випадку, максимальне (мінімальне) число уявного діапазону, залежить від основи системи числення і кількості виділених розрядів n: N(q) _max = (qⁿ-1), N(q) _min = - (qⁿ-1). Наприклад, три розряди десяткової системи забезпечать діапазон чисел (з урахуванням знаку) N_min= -999, N_max= 999.

3.2 Вибір системи числення комп’ютера

 

3.2.1 Переваги двійкової системи

Розробку комп’ютера починають з вибору системи числення, методів виконання арифметичних і логічних операцій, елементної бази. Ці питання є важливими, оскільки повинні забезпечити задану точність і швидкість обчислень, надійність в роботі, діапазон чисел.

Вибір системи числення у великій мірі обумовлюється наступними основними причинами:

1. Основу системи визначає число знаків (їх зображень) в одному розряді. Тут перевагу має двійкова система, а не десяткова оскільки вона вимагає всього два знаки (стани), а десяткова - десять. Елементи, з десятьма станами (декатрони), що є в наш час, мають малу швидкість перемикання, громіздкі, мають невисоку надійність в роботі.

2. З одного боку система числень повинна забезпечити простоту арифметичних операцій, а з іншого великий діапазон уявних чисел. Ці дві суперечності вирішуються на користь простоти арифметичних операцій при представленні чисел. Насправді, в двійковій системі не треба додаткових пристроїв представлення чисел. Сам сигнал несе інформацію про число і має двійкову природу: є сигнал або його немає - "1 " або "0". Крім того, майже всі елементи електронних схем (є струм/ напруга або ні) мають двійкову природу (реле, діод, транзистор, тригер, фотоприймач, стан оптоволокна, ін.).

Якщо прийняти показник ефективності системи з погляду витрат устаткування:

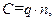
де q - основа (глибина) системи, n – довжина (розрядність) системи.

Розрядність n визначається з діапазону уявних чисел. Максимальне число з основою q: 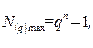звідси знайдемо n:

n=log_q( N_{(q) max} + 1),

тоді витрати на устаткування підраховують за формулою:

C = q log_q (N(q) _max + 1).

Якщо за одиницю устаткування прийняти умовний елемент з одним стійким станом, то можна порівняти системи числення з погляду витрат.

Графік відносного показника приведений на рис. 3.2.

Рисунок 3.2 - Відносні витрати при різних значеннях основ

Наймінімальніші витрати будуть при основі е = 2,72, тобто, з погляду витрат, виходить найекономнішою буде система з q=3. Вона застосовується в ЕОМ "Сетунь". Проте, більшість ЕОМ використовують двійкову системи через простоту арифметичних операцій в ній.

Розглянемо це на прикладі складання в цій системі:

0+0=0, 1+0=1, 0+1=1, 1+1=10.

Складання цілих чисел без знаку представлено схемою (рис. 3.3).

Приклад. Знайти С=А+В. А=+1011 (+11); В=+1001 (+9); С=+10100 (+20).

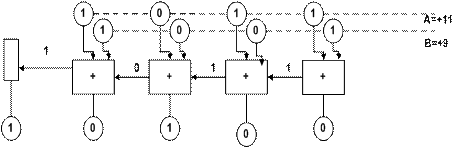Рисунок 3.3 - Структурна схема бінарного (двійкового) суматора

 

Множення проводиться в двійковій системі ще простіше: 0×0=0, 0×1=0, 1×0=0, 1×1=1.

 

4 МЕТОДИ ПЕРЕКЛАДУ ЧИСЕЛ З ОДНІЄЇ ПОЗИЦІЙНОЇ СИСТЕМИ ЧИСЛЕННЯ В ІНШУ

Раніше ми відзначали, що будь-яке число можна представити поліномом з основою q₁, але це ж число можна представити іншим поліномом (див. рис. 3.3) з основою q₂, інакше: N(q₁)= N(q₂). Представимо це для загального числа (що має цілу і дрібну частини - неправильний дріб) у наступному вигляді: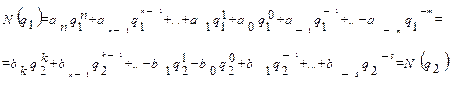

4.1 Методи перекладу цілих чисел

 

4.1.1 Метод підбору коефіцієнтів

Завдання перекладу числа з основою q₁ в число з основою q₂ зводиться до відшукування коефіцієнтів полінома нової основи. Цю задачу можна вирішити методом підбору коефіцієнтів полінома.

Правило. На початку беремо число з максимальною степінню основи, перевіряємо її вхід до даного числа так, щоб воно не перевищувало задане, потім підбираємо коефіцієнти менших степіней полінома, так щоб сума давала початкове число. Всі дії повинні виконуватися за правилами q_і-ї арифметики, тобто за правилами початкової системи числення.

Наприклад. Перевести десяткове число 96 у трійкову систему.

Рішення. 96 = 0×3⁵+1×3⁴ + 0×3³+1×3²+2×3¹ + 0×3⁰ = 010120₍₃₎

Проведемо перевірку методом підстановки значень ваги розрядів, множення його на підібраний коефіцієнт і обчислення загальної суми.

96=0×243 + 1×81 + 0×27 + 1×9 +2×3 + 0×1.

Цей прийом застосовується тільки при "ручних" перекладах. Машинні алгоритми використовують метод ділення на основу нової системи числення.

 

4.1.2 Метод ділення на основу нової системи

Поліном цілого числа N(q₁) можна записати за схемою Горнера в іншому вигляді:

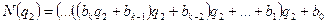
де b₀…b_k -коефіцієнти молодшого b₀, старшого b_k розрядів числа N(q₂).

Якщо праву частину розділити на q₂, то отримаємо цілу частину (у лапках) і залишок з b_і (0<i<k). Повторюючи ділення k+1 разів отримуємо кожного разу залишки b₁, b₂, ..., b_к і цілі частини. Останній залишок b_к є старшим розрядом залишку числа, представленого в основі q₂ (неподільний залишок).

Приклад. 12₍₁₀₎ перевести в бінарну (двійкову) систему числення.

Рішення. Ділимо на q=2 (у дужки поміщений залишок):

 

 

Частка (1) менше основи 2, тому це теж залишок, причому старший, тому припиняємо ділення. Відповідь: 1100 (12₍₁₀₎).

 

4.1.3 Метод ділення на основу в будь-якій позитивній степіні

Попередній метод має один недолік. При великих числах, операція ділення має багато ітерацій. Це знижує швидкодію. Метод ділення на основу нової системи в будь-якому позитивному степіні аналогічний попередньому. Тут беруть для ділення число (з новою основою q_k) близьке до заданого числа N(q_i), але що не перевищує його. Кожен залишок від ділення записують в двійкових розрядах, число яких рівне узятому степіні.

Наприклад. Перевести в бінарну систему числення число N=523 _(10).

Рішення. Вибираємо, найближче до заданого, число 2⁹ = 512 і ділимо:

523 : 512=1(залишок 11).

Отримали два залишки: старший - 1, молодший - 11. Кожний із залишків розписуємо в дев’яти бінарних розрядах: 1000000000 і 000001011. Потім сполучаємо (додаємо) записи (старші нулі можна не записувати) і отримуємо результат- число 1000001011.

В двійковій системі (для цілого числа) b₀ завжди «0» або «1». В першому випадку N(q₂) - це парне число, в другому - непарне.

 

4.1.4 Метод віднімання найближчих, менших степінних ваг

Метод полягає в наступному. Вибирають значення найближчої, розрядної ваги бінарного (двійкового) числа, менше заданого.

Віднімаючи його від заданого числа, отримують залишок. У розряді вибраної ваги, ставиться 1. Потім порівнюють залишок з новим меншим ваговим розрядом. Якщо залишок менший, то в цьому ваговому розряді ставиться 0, якщо залишок більший, то в цьому розряді ставиться 1, а із залишку віднімається вага цього розряду. Виходить новий залишок, який знову порівнюється з наступними меншими вагами. Так продовжується до останнього (молодшого) вагового бінарного розряду і отримають число.

Приклад. Перевести десяткове число 1125 в двійкове. Метод - віднімання менших найближчих розрядних ваг. Найближчою меншою розрядною вагою буде число 1024=2¹⁰. Ставимо в десятому розряді 1 (зліва від коми, де міститься 2¹⁰).

Віднімаємо 1125-1024 =101, де 101 - десятковийзалишок, який порівнюємо з числом 2⁹= 512. Залишок 101 менше 512, це означає, що на місці 2⁹ ставимо 0. Порівнюємо наступну розрядну вагу 2⁸= 256>101. Знову на місці розрядної ваги 2⁸ ставимо 0. Аналогічно буде і для розряду 2⁷ - ставимо 0. Порівнюємо наступну розрядну вагу 2⁶=64<101. У цьому розряді ставимо 1 і віднімаючи 101-64=37 отримуємо новий залишок, який порівнюємо з розрядною вагою 2⁵=32<37. В цьому розряді ставимо 1, і віднімаючи 37-32=5, отримуємо новий залишок, який легко розписати в чотирьох розрядах, що залишилися: 0101. Таким чином, отримуємо число 10001100101₍₂₎=1125_(10). Перевіримо: 1024+64+32+4+1=1125.

Метод виключає громіздку операцію ділення і при невеликому досвіді легко виконується користувачем. Метод придатний для перекладу як цілої, так і дробової частини числа.

 

4.2 Переклад правильних дробів множенням на основу системи числення

Дробову частину числа можна записати в новій системі:

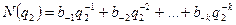, (4.1)

цей вираз можна переписати по схемі Горнера:

.

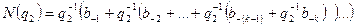Якщо праву частину множити послідовно на q₂, то знаходитимемо новий неправильний дріб, в цілій частині якої будуть числа b_-1, b_-2, ..., b_-k, при цьому всі дії повинні виконуватися за правилами q₁-арифметики, і отже в цілій частині дробів, що виходять, з’являтимуться еквіваленти чисел нової системи числення, записані в початковій системі числення.

Приклад: Перевести десятковий дріб 0,625 в двійкову систему числення. Рішення:

0,	625×2
	250×2
	500×2
	000×2

Відповідь: N= 0,1010. Перевірити за формулою 4.1.

Правило: для перекладу правильного дробу (без цілої частини) необхідно, діючи в арифметиці початкової системи числення, помножити число, що переводиться, на основу нової системи, у результату відокремити цілу частина, а дробову частину, що залишилася, знову помножити на цю основу і так до отримання потрібного числа значущих цифр. Результат записувати як 0, ... і дробову частину у порядку отримання.

Приклад. Перевести двійковий дріб 0,1101 в десятковий.

Рішення:

	0,	1101×1010
b-1	1000,	0010×1010
b-2	0001,	0100×1010
b-3	0010,	1000×1010
b-4	0101,

 

Відповідь: N=0,8125.

При перекладі правильних дробів з однієї системи числення в іншу, може вийде дріб у вигляді нескінченного ряду або ряду, що розходиться. Тому, процес перекладу необхідно закінчувати:

- при появі в дробовій частині по всіх розрядах нулів;

- якщо буде досягнута задана точність дробу (тобто необхідне число роз рядів).

Приклад. Перевести дріб 0,543 з шісткової системи в трійкову.

Рішення:

0,	543(6)×3
2,	513×3
2,	343×3
1,

Відповідь: N = 0,543₍₆₎ ~0,221₍₃₎=0,532₍₆₎

 

4.3 Переклад неправильних дробів

Правило. Для перекладу неправильного дробу (тобто такого дробу, що містить цілу частину) з однієї системи числення в іншу необхідно здійснити роздільно переклад її цілої і дробової частин, а результати записати послідовно, відокремивши цілу частина від дробової комою. Наприклад: 98,625₍₁₀₎ дорівнює 1100010,1010_(2).

4.4 Переклад з 16-ої і 8-ої систем в 2-ву і навпаки

При перекладі чисел з десяткової системи в 2-ву, часто викорис-товують проміжну 8-ву систему. Це дає економію в числі операцій.

Таблиця 4.1 - Перевод у бінарну систему

q2=8	q2=2
Число	залишок	число	залишок	тріада
3 кроки
			7 кроків

Приклад. Перевести десяткове число 121 в двійкове (див. табл. 4.1) через проміжну 8-у систему. Для порівняння наведен переклад через основу q=2.

 

Правило. Щоб перевести число з 16-ї і 8-ї системи в 2-у необхідно кожну цифру числа, що переводиться, представити відповідно чотирирозрядним або трирозрядним двійковим кодом (тетрадами або тріадами), розташував їх на місцях (розрядах) цих цифр. Нулі в старших і молодших розрядах, що не змінюють значення числа можна опускати.

 

Приклади: 171₍₈₎ в двійкове N=001 111 001;

753,335₍₈₎ в двійкове

N=111 101 011,011 011 101.

Правило. Для перекладу чисел з двійкової системи числення в шістнадцяткову (вісімкову) слід двійкові цифри числа, що переводиться, згрупувати по чотири (три) в обидві сторони від коми (при необхідності неповні групи доповнити нулями), кожну групу двійкових цифр замінити відповідною їй цифрою в новій системі числення. Нові цифри розташувати на місцях замінюваних кодів.

 

Приклад: 111111010,1100001001₍₂₎ перевести в 16-у і 8-у системи числення.

а) 0001 1111 1010 , 1100 0010 0100₍₂₎

1 F А , 3 2 4₍₁₆₎

Відповідь: 1FA,C24₍₁₆₎

б) 111 111 010, 110 000 100 100₍₂₎

7 7 2 , 6 0 4 4 ₍₈₎

Відповідь: 772,6044₍₈₎

 

Узагальнюючи, робимо висновок: у якості проміжних систем числення, доцільно використати системи з основою q=2^k, для спрощення перетворення їх в двійкову систему і навпаки (де цифри замінюють їх еквівалентами).

 

4.5 Переклад двійково-десяткових систем числення

Двійкові розряди розбиваються на тетради з вагою розрядів наприклад, 8421, а в тетрадах записують цифри від 0 до 9 у двійково-десяткових кодах, тобто 1 треба ставити у тих розрядах, вага яких враховується в записуваній цифрі. Переклад з однієї системи до іншої проводять по тетрадах.

Приклад: N=995₍₁₀₎ ® 1001/1001/0101.

 

4.6 Форма представлення чисел в комп’ютері

У десятковій системі існують багато форм представлення чисел. Ми, вміло користуючись цим, самі вибираємо ту або іншу форму представлення чисел. Наприклад, число 0,25 можна уявити, як 1/4, коли виконуємо операції з такими ж дробами. Можна уявити, як 25×10^-2 або 2500×10^-4 або 0,0025×10² або 0,3 при округленні і т.д.

Всю різноманітність запису чисел розбивають на природні і нормалізовані (нормальні) форми.

Нормалізованою формою запису будь-якого числа N звичайно називають математичний вираз типу N=±0,mхq^(±n), де ±m – мантиса (у вигляді правильного дробу зі значенням у старшому розряді, що не дорівнює «0»), q - основа, ±n - порядок числа.

При природній формі, число записують в натуральному вигляді, наприклад: для позитивних чисел: 125 (ціле число); 0,125 (правильний десятинний дріб); 125,125 (неправильний десятинний дріб). При норма-лізованій формі запису одне і те ж число може приймати різний вигляд і його форма залежить від прийнятих правил (обмежень), що діють при записі. Наприклад, 12500 може бути записано 12,5 ×10³ =0,125×10⁵= 125000×10^-1 і т.д.

Така різноманітність форм представлення чисел є причиною ускладнення пристроїв і алгоритмів функціонування ЦА обчислювачів.

Щоб уникнути цього, в ЦА прийняті свої нормалізовані форми запису і відображення чисел, що дозволяють мінімізувати вартість апаратних і алгоритмічних засобів.

5 ФОРМАТИ ПРЕДСТАВЛЕННЯ ЧИСЕЛ В КОМП’ЮТЕРІ

5.1 Представлення чисел з фіксованою комою (крапкою)

Автоматне зображення числа – це представлення числа N в розрядній сітці ЦА, в наперед заданому форматі і правилами відображення. На рис. 5.1 представлений звичайний машинний формат числа з фіксованою комою на n-розрядів (для знакової частини числа надано один додатковий розряд Sg1).

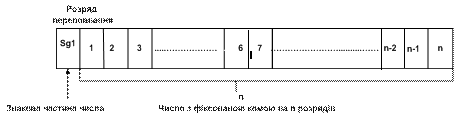Рисунок 5.1 - Формат машинного представлення числа з фіксованою комою (крапкою) - ФФК

При представленні числа у форматі з фіксованою комою (ФФК) в двійковій системі числення увесь формат n-розрядної сітки розбивається наперед на дві основні частини-знакову і числову:

- один (або два зліва) розряди для представлення знаку числа (0 або 00 плюс «+»; 1 або 11 мінус «-»);

- наступні k розрядів визначають для розміщення цілої частини числа;

-інші (n-2-k) розрядів відводять для розміщення дробової частини числа.

Дійсно, положення коми строго фіксоване в розрядній сітці ЦА.

Позначимо машинне зображення числа N через N_m, тоді число N_m дорівнює: ,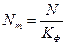

де К_ф - масштабний коефіцієнт прийнятого формату, величина якого залежить від числа розрядів цілої частини, тобто для рис 5.1 K_Ф=2^k=2⁶.

Приклад. Записати число N=+11,00111000111 (природний запис) у форматі машини з К_Ф=2⁶, кількість розрядів n=16. N_m= N×2^-6.

[N]_m=0/000011,001110001 (машинний запис числа N, останні два розряди 11 - втрачені із за відсутності знакомісць для їх розміщення).

Для сприйняття машинної форми числа N_m знакову його частину (крайні зліва один або два розряди) відокремлюють знаком «слеш» / чи .

Навпаки, число N визначається як N=N_m×K_Ф=+11,001110001. Знак «+» для позитивного числа (природний запис) не записується.

Діапазон уявних чисел залежить від обраного формату цілої частини і складає:

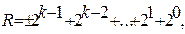
де k - кількість розрядів числа.

При записі чисел у форматі з фіксованою комою, якщо число виходить за межі розрядної сітки числа, молодші розряди відкидаються. При цьому, можуть виникати значні погрішності, зокрема, ділення на «0», що приводить до невизначеності і необхідності втручання у розрахунки. Проте, при роботі ЕОМ у форматі з фіксованою комою швидкість виконання арифметичних і логічних операцій висока.

Помилка представлення чисел зменшується при правильному виборі (розрахунку) масштабних коефіцієнтів К_Ф. У деяких ЦА при переповненні розрядної сітки автомата, виводять один розряд «переповнення» із зупинкою розрахунків, що порушує його нормальне функціонування. (Наприклад, у ЄС ЕОМ ХХХХ АЛП виконуються операції окремо з цілими числами і дробами, а переповнення від складання дробів додається до цілої частини).

5.2 Представлення чисел у форматі з рухомою комою (ФРК)

Іншою найбільш поширеною нормальною формою є представлення чисел у формі з рухомою комою. В цьому випадку в нормальній формі число записується як

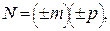
N - нормалізоване число; m - мантисса, а р - характеристика (порядок) числа.

Таке уявлення, в загальному випадку, не є однозначним. Тому, для нормалізованого числа вводять, як правило, обмеження. Найбільш зручною і поширеною є вимога вигляду:

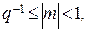(5.1)

де q - основа системи.

Правило.Нормалізованою формою представлення чисел є форма числа, для якої справедлива умова 5.1.

В цьому випадку абсолютне значення мантиси може бути в межах від 0,q^-1 до (0,q^-1+0,q^-2+…+0,q^-n), тобто до 1 при n→∞, де n - кількість розрядів для запису мантиси без знаку.

Розташування коми у числі, мантису якого помножено на порядок, не є постійним. Тому і форма запису називається з рухомою комою (крапкою).

Формат машинного відображення чисел з рухомою комою представлений на рис. 5.2 для 16-и розрядної сітки.

 

Зн. мант. Мантиса Зн. поряд. Порядок

 

Рисунок 5.2 - Формат машинного представлення числа з рухомою комою (крапкою)

Формат уявлення цілої частини числа визначається знаком порядку і числом порядку і може змінюваватися. Але завжди формат числа повинен містити: знак числа, мантису, знак порядку, порядок (де порядок визначає скільки розрядів мантиси необхідно відлічити вправо або вліво, щоб поставити кому, яка відокремлює дробову частину у кінцевому вигляді числа).

Отже, перш ніж записати число в ЦА з його розрядною сіткою, це число нормалізують, тобто приводять до вигляду, коли в старшому розряді мантиси немає «нуля», а є «одиниця» (для двійкової системи числення). Решта всіх форм називається ненормалізованими.

Порядок - це показник степіні для обранної системи числення, на який потрібно помножити (для позитивного знаку порядку) або розділити (для негативного знаку порядку) мантису для перетворення, тобто, Р=q^±p,

де Р - число, яке записане в двійкових розрядах порядку. При нормалізації число зрушують порозрядно вправо (якщо є ціла частина числа) або вліво (до одиниці після коми). При зрушенні вправо порядок (тобто степінь основи) збільшується з кожним зрушенням на 1. При зрушенні вліво порядок зменшується кожного разу на 1.

Приклади. Записати двійкове число в нормальній формі (звичайний машинний код-один розряд під код знаку):

+11101,011 (природна форма); 0,11101011×2⁺⁵ (напівмашинна форма); 011101011101(звичайний машинний код).

Для прийнятого формату (рис.5.2) число запишеться у машинній формі (модифікований машинний код- два розряди під код знаку):

 

Зн. мант. Мантиса Зн. поряд. Порядок

 

При записі мантиси зручно щоб старший розряд був зліва, а в полі порядку розташування старшого розряду обумовлено коментарем (визначено для окремого ЦА особливо). Приклад:

+0,00011111 (природна форма) = 011111×2^-3 (напівмашинна форма) = 011111000100011 (звичайний машинний код, наявність коми припускається, але в ЦА вона за «слешем» відсутня).

Оскільки основа 2₍₁₀₎=10₍₂₎ завжди постійна, то її запис в характеристиці числа опускається, а діапазон уявних чисел визначається розрядною сіткою.

Максимальне уявне число буде при позитивних знаках мантиси і порядку, і при максимальних значеннях їх чисел, іншими словами, при запису числа - по всіх розрядах одиниці. Швидкість обчислень у ФРК менша ніж у ФФК, а точність і діапазон - вища.

Мінімальне уявне число має негативні знаки мантиси і порядку, при мінімальному значенні мантиси і максимальному (тобто одиниці по всіх розрядах) порядку.

,

.

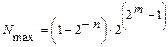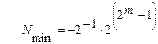5.3 Погрішності представлення чисел

Представлення чисел в ЦА, як ми бачимо, завжди спричиняє за собою появу погрішностей в розрахунках, величина яких залежить від обмежень, що накладаються на автомат по розрядній сітці та формі представлення чисел.

 

5.3.1 Абсолютна похибка представлення чисел DN

Абсолютна похибка представлення чисел DN називається різниця між дійсним значенням числа N_і та його значенням N_m, отриманим після машинного відображення, операцій АЛП.

Приклад: двійкове число +11,00111000111 при n=15 і K_Ф=2^k, k=6, тоді N_m = 000011,001110001 [останні два розряди 11 - втрачені]. Перевівши в десяткові числа, отримаємо:

N =11,00111000111 (+3,2221678);

N_m =000011,001110001 (+3,2207031);

DN =N–N_m = +3,2221678– (+3,2207031)= +0,0014647.

Правило. Максимальна похибка DN для чисел формату з фіксованою комою не перевищує одиниці молодшого розряду сітки:

,

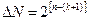де n - розрядність автомата;

k - степінь масштабного коефіцієнта К_Ф;

N_m - значення машинного числа в двійковій системі після його переводу (тобто з N в N_m).

 

5.3.2 Відносна похибка представлення числа dN

Відносна похибка представлення числа dN. Це відношення абсолютної погрішності DN до числа N в процентному відношенні, тобто: .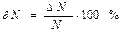

Зазвичай N визначається математично після виконання арифметичних операцій в десятковій системі.

Після визначення абсолютної погрішності визначаємо відносну похибку в %. Приклад: з попереднього рішення DN=0,0014647, тоді

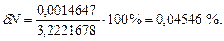
6 БІНАРНА (ДВІЙКОВА) АРИФМЕТИКА

У арифметиці будь-якого типу беруть участь завжди два або більше чисел. Як результат виконання арифметичних операцій з’являється нове число. Формально це можна представити у вигляді:

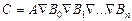, (6.1)

де 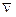- знак будь-якої арифметичної дії з чотирьох: складання, віднімання, множення, ділення.

Будь-яке з чисел А, B₀, B₁, B_n є операндами, тобто числами, що беруть участь в арифметичних операціях, які виконуються ЦА.

Необхідно звернути увагу на те, що у виразі 6.1 опущено індекс m - машинне число. Але всі операнди і результат С є машинними числами. Правила виконання арифметичних операцій на рівні розрядів операндів:

,

,

,

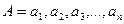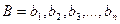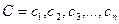де n - розрядна сітка автомата.

Алгоритми виконання арифметичних операцій в системі числення з основою q аналогічні алгоритмам в десятковій системі числення.

Результат виконання операції Ñ цифр а_i та b_i в i-м розряді представляється двома цифрами: цифрою C_i - результатом відповідної операції в даному розряді та цифрою П_i - перенесенням в старший розряд або позики зі старшого розряду (при відніманні).

Результат C_i і перенесення П_i формуються за наступними правилами:

Додавання:

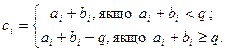
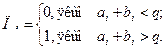
Віднімання:

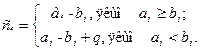
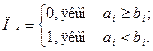
Множення:

 

Виконання операції не може бути зведене до операції над окремими цифрами розрядів. Тому ділення виконується по аналогії з діленням в десятковій системі.

Двійковий напівсуматор (HS)- пристрій, що виконує арифметичну дію складання без урахування переносу П_i з попереднього розряду, тобто на його вхід подаються тільки числа розрядів a_i та b_i без переносу П_i (наприклад, наймолодші розряди операндів А і В).

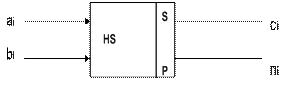
Рисунок 6.1 - Двійковий напівсуматор

Правила складання напівсуматора можна представити у вигляді таблиці 6.1, що має назву таблиця істинності (ТІ).

Таблиця 6.1 - Напівсуматор

ai	bi	ci	Пi

Тут порозрядне складання виконується за формулою:

a_i + b_i = C_i + П_i ,

де а_i, b_i - розряди чисел А, В;

C_i - сума і-го розряду;

П_i - перенос у наступний розряд.

Але не враховувати переносів при складанні багаторозрядних чисел не можна.Тому, при складанні користуються пристроєм, що має назву двійковий суматор. Це пристрій, що виконує арифметичні дії складання з урахуванням переносу (П_i-1). від попереднього розряду і передачі переносу (П_i). в наступний розряд. Його робота і структурна схема була розглянута в розділі 3 (рис. 3.3).

ТІ двійкового суматора представлена в таблиці 6.2.

Таблиця 6.2 - Суматор

ai	bi	П(i-1)	Ci	Пi

Тут порозрядне складання виконується за формулою:

a_i+b_i+П_i-1=C_i+П_i,

де а_i, b_i - розряди чисел А, В;

C_i - сума і-го розряду;

П_i-1 - перенос з попереднього розряду;

П_i - перенос у наступний розряд.

При виконанні арифметичної операції- віднімання в двійковій системі числення (в десятковій- аналогічно), нерідко проводиться позика, рівно-сильна відніманню одиниці зі старшого розряду. Запозичення зі старшого розряду еквівалентно додаванню до молодшого розряду величини основи.

Крім того, цю позику необхідно враховувати при відніманні цифр наступного старшого розряду (тобто чи була позика в молодшому розряді). З урахуванням цього, і пам’ятаючи, що від’ємник завжди повинен бути менше зменшуваного можна представити правила у вигляді таблиці 6.3.

Таблиця 6.3 – Від’ємник бінарних чисел

ai	bi	Zi	Ci	Z(i+1)
		-1 -1 -1 -1		-1 -1 -1 -1

 

Порозрядне віднімання виконується за формулою:

а_i – b_i + Z_i = C_i + Z_i+1,

де a_i, b_i – операнди розряду;

C_i – різниця розряду;

Z_i – позика із молодшого і-го розряду;

Z_i+1 – позика у старшого розряду.

 

Порівняння даних табл. 6.2 і 6.3 свідчать про те, що при відніманні операнду В від А порозрядно АЛП повинен мати додаткові розряди для зберігання знаку «–» для Z_i , Z_(i+1) що ускладнює схему АЛП (при тому що a_i, b_i і С мають знак «+»). Тому перевагу надано двійковому суматору.

Розглянемо приклади на складання і віднімання для чисел з фіксованою комою (ФФК). Оперуватимемо з шестизначними, позитивними числами за модулем менше одиниці.

Приклади: а) виконати операцію складання бінарних чисел +А і +В (двох операндів А і В):

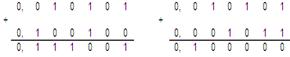
б) виконати операцію віднімання бінарних чисел +С і -D (двох операндів С і D):

в) віднімання в 8-ій системі: г) віднімання в 3-ій системі:

д) виконати операцію множення бінарних чисел +Е і +F:

е) виконати ділення бінарних чисел +G і +H (у вигляді неправильного дробу +G і цілого числа +H):

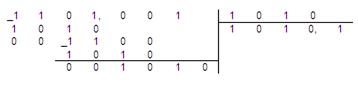
Проте, таке віднімання, ділення і множення для автоматів є складним оскільки при виконанні цих операцій в обчислювальних ЦА виникає проблема представлення негативних чисел. Для машинного представлення негативних чисел використовуютькоди: прямий, обернений і доповняльний.

Одним із способів виконання операцій за допомогою двійкового суматора, є заміна операції віднімання операцією суми із оберненим або доповняльним кодом негативного числа:

А–В= А + (-В)=А+В*.

Заміна віднімання складанням ставить проблему представлення негативного числа в цифровому форматі. Це може бути вирішєно, наприклад, за допомогою використання властивості циклічності чисел при їх переліку, рахунку, зображенні (два, три, …, дванадцять, тринадцять…).

7 КОДИ БІНАРНИХ ЧИСЕЛ

 

Развернуть

Открыть в широком формате