рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Транспорт
- /
- Множення чисел на ДСОК при негативному множнику
Реферат Курсовая Конспект
Множення чисел на ДСОК при негативному множнику
Множення чисел на ДСОК при негативному множнику - раздел Транспорт, ПРИКЛАДНА ТЕОРІЯ ЦИФРОВИХ АВТОМАТІВ Випадок В<0. Якщо Множник Негативний, То Добуто...
Випадок В<0. Якщо множник негативний, то добуток чисел на суматорі ДСОК є додатком виправленя [`А ] і [A]об×2-n до отриманого добутку обернених кодів співмножників.
Доказ. Нехай А=[A]об і В<0, тоді 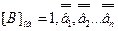 ; відповідно до подання у ФРК, фіксовано перед старшим розрядом |B|+[B]об=q-q-n=2-2-n; звідси [В]об=2+В-2-n; тож,
; відповідно до подання у ФРК, фіксовано перед старшим розрядом |B|+[B]об=q-q-n=2-2-n; звідси [В]об=2+В-2-n; тож, + 2-n-1, добуток дорівнює: А×В =Aоб×
+ 2-n-1, добуток дорівнює: А×В =Aоб× +[A]об× (-2-n)+
+[A]об× (-2-n)+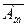 ; є два виправлення: перше [A]об×(-2-n) порівняне мале (тому часто ігнорується) і друге +
; є два виправлення: перше [A]об×(-2-n) порівняне мале (тому часто ігнорується) і друге +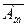 .
.
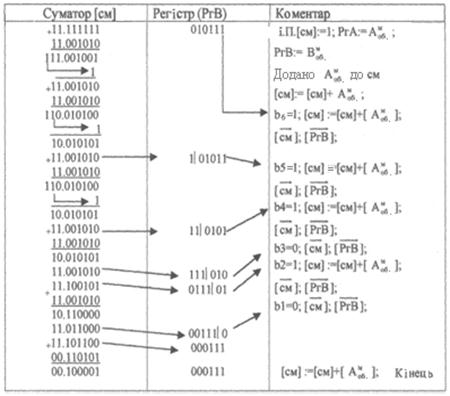
Алгоритм. Множення на ДСОК (при В<0) виконується в наступній послідовності (наведена в таблиці 13.2):
- у суматор записуються 11.111...1 (машинний нуль оберненого коду);
- у регістр В записується множник у оберненому коді (без знака);
- у суматор додається множене у оберненому коді Аоб;
- ведеться аналіз розрядів РгВ (починаючи з молодшого), і якщо там «1» («0»), то до вмісту суматора додається (нічого не додається) обернений код множеного;
- після циклу додавання і аналізу робиться зсув вправо вмісту суматора і РгВ на один розряд (можна з переносом молодших розрядів суматора в старші розряди РгВ);
- після аналізу і зсуву старшого розряду множника до результату додають виправлення [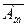 ] - інверсію Аоб, включаючи і знак;
] - інверсію Аоб, включаючи і знак;
- якщо знак результату негативний, то він у оберненому коді і необхідне перетворення у прямий код;
- після перетворення в прямий код, необхідно перевірити нормалізацію результату.
Приклад. Метод 2, множення чисел на ДСОК. А=-0/110101; В=-0/101000; А×В=+2120. Рішення: Запишемо машинне зображення чисел.
Амоб = 11/001010; Вмоб = 11/010111; 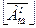 = 00/110101.
= 00/110101.
Послідовність виконання операції множення наведена в таблиці 13.2.
З урахуванням розрядів РгВ будемо мати 100100001000111. Переповнення «1» із знакового розряду Sg1 додається до молодшого розряду числа. Тоді, одержимо відповідь: Спр=00100001001000=2120(10).
Існує ряд методів множення заснованих на роздільному під-сумковуванні груп часткових доданків з наступним об’єднанням сум з урахуванням переносів. Роздільна обробка проміжних сум і переносів вимагає так званого "дерева суматорів" (використано в IBM-360).
Таблиця 13.2 - Множення на ДСОК при негативному множнику
Існують також прискорені методи множення, засновані на використанні матриць проміжних результатів. Розглянемо схему множення:
A = a5, a4, а3, а2, a1
*B = b5, b4, b3, b2, b1
a5b1 а4b1 а3b1 а2b1 а1b1
+.........................................
а5b5 а4b5 а3b5 а2b5 а1b5
С10 С9.......................С2 С1
Цю схему можна представити також у вигляді матриці таблиці 13.3. Кожний елемент цієї матриці дорівнює "0" або "1".
Таблиця 13.3 Матричне множення чисел

Добуток двох чисел можна одержати, якщо підсумувати елементи матриці в діагональному порядку. Cкладати доводиться тільки 0 або 1, тому операцію додавання можна виконувати за допомогою напівсуматорів і суматорів на один двійковий розряд.
 Рисунок 13.1 - Структурна схема пристрою множення для реалізації матричного алгоритму
Рисунок 13.1 - Структурна схема пристрою множення для реалізації матричного алгоритму
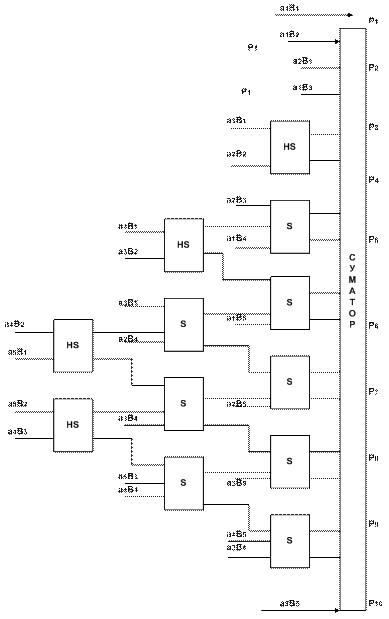
Рисунок 13.2 - Схема множного пристрою за алгоритмом Дадда
Найбільше поширення одержали алгоритми Дадда, Уоллеса (матричний) і алгоритм збереження переносів [1-21]. На рис. 13.1 представлена структурна схема матричного пристрою множення для реалізації матричного алгоритму.
Алгоритми відрізняються друг від друга групуванням часткових добут-ків, кількістю етапів перетворень. Для матричного алгоритму - чотири етапи перетворення, для алгоритму Дадда – три етапи. Однак, матричні методи множення, незважаючи на більший об’єм устаткування, дають великий виграш часу, а використання ВІС значно знижує обмеження на устаткування.
Розглянуті методи множення знайшли широке застосування в практиці бінарної арифметики.
14 ДІЛЕННЯ БІНАРНИХ ЧИСЕЛ
14.1 Методи ділення бінарних чисел
Найбільше поширення одержали наступні методи виконання операції ділення чисел:
1. На кожному кроці з діленого віднімається дільник (починаючи зі старших розрядів) стільки разів, скільки це можливо до одержання залишку менше дільника. У частці записується цифра, рівна числу цілих частин дільника N. L - залишок. A: B= N×B+L
2. Інший метод ділення полягає в множенні діленого на обернену величину З=А:В=А×В-1=А×1/В.
Тут виникає проблема знаходження обернених величин шляхом розкладання в біноминальний ряд Ньютона, використовуючи модель розкладання бінома ступеня m:
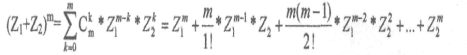 де Ckm - біномінальні коефіцієнти число різних сполучень із m різних змінних по k у кожному сполученні:
де Ckm - біномінальні коефіцієнти число різних сполучень із m різних змінних по k у кожному сполученні:

3. У третьому методі використовують наближені формули знаходження частки, які зводять операцію розподілу до операції додавання, вирахування, множення.
Перший розглянутий метод відносять до “шкільних” алгоритмів ділення з відновленням залишку. Розглянемо приклад розподілу в бінарній арифметиці.
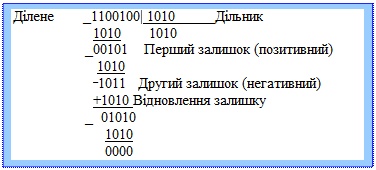 |
Приклад: Ам=00/1100100. (100(10)); Вм=00/1010. (10(10)). Рішення наведене нижче (використано правила бінарного віднімання).
 |
14.1.1 Алгоритм ділення з відновленням залишку
Формально алгоритм описується в такий спосіб. Нехай А - ділене, В - дільник, С - частка: A=0,α1α2...αn; B=0,b1b2...bm, C=0,c1c2...cr.
На кожному кроці визначається залишок Аi=Ai-1-B×2-i, проводиться аналіз: якщо залишок Аi>0, то в старший розряд частки записується Ci=l, робиться лівий зсув і перехід до визначення наступного залишку. Якщо Ai<0, то Сi=0 і відновлюється залишок Ai=Ai-1+B×2-i, а на наступному кроці після зсуву визначається новий залишок і т.д.
Даний алгоритм ділення з відновленням залишку реалізується на двійкових суматорах оберненого (ДСОК) або доповняльного (ДСДК) кодів. Структурна схема наведена на рис. 14.1.
Частковий залишок (частка) виходить в результаті послідовного виконання операції віднімання (із заміною віднімання на додавання в доповняльному коді), тому частіше застосовується суматор ДСДК для алгебраїчного додавання.
 |
Рисунок 14.1 - Структурна схема ЦА операції ділення
14.2 Ділення чисел з фіксованою комою з відновленням залишку
Ділення виконується за алгоритмом із відновленням залишку на суматорі доповняльного коду (ДСДК) у наступній послідовності:
- визначається знак частки по формулі SgС=SgАÅSgВ;
- проводиться подання діленого і дільника в машинних кодах, коли ділене завжди, незалежно від його знака, береться в прямому коді з позитивним знаком, а дільник завжди, незалежно від його знака, береться у доповняльному коді з негативним знаком;
- усунення дробової частини в дільнику, шляхом переносу коми вправо на n розрядів (за аналогією з десятковою системою числення). Щоб дріб не змінився, у діленому також переносять вправо кому на n розрядів;
- починаючи зі старших розрядів, до діленого додають дільник у доповняльному коді, що рівнозначно вирахуванню з діленого дільника й аналізують знак проміжного залишку:
1) якщо знак проміжного залишку 00 (позитивний), то в регістр частки РгС записується 1, починаючи зі старшого розряду. Залишок зсувається на один розряд вліво (просто знакову крапку перенести вправо на один розряд), зноситься наступний розряд діленого (що не брав участь до цього в ділені). Після цього, проміжний залишок підготовлений до наступного додатка діленого у доповняльному коді;
2) якщо знак проміжного залишку 11 (негативний), то в регістр частки РгС записується 0, починаючи зі старшого розряду. Залишок відновлюється шляхом додатка до нього дільника в прямому коді з позитивним знаком. Відновлений залишок зсувається вліво на один розряд (крапку, що відокремлює знак, перенести вправо на один розряд), зноситься наступний розряд діленого (що не брав участь до цього в ділені). Після цього, проміжний залишок підготовлений до наступного додатка дільника у доповняльному коді;
- дії попередніх пунктів повторюються до одержання машинного нуля або заданої точності обчислення (кількість розрядів дробу після коми за цілою частиною числа). Кома дробу встановлюється в частці С після зносу останнього розряду цілої частини діленого.
- результат ділення представлений у регістрі частки С в прямому коді.
Знак результату привласнюється відповідно до пункту 1.
Приклад. Розділити число А= -100111(-39) на В= -11(-3), представлених у (ФФЗ) . Розрядність суматора і регістрів дорівнює 6.
Рішення: Операція робиться на ДСДК (модифікований код) за алгоритмом із відновленням залишку.
1. Визначаємо знак частки: SgС=SgАÅSgВ =1Å1=0. Знак позитивний.
2. Записуємо машинні зображення чисел: Ампр=00/100111; Вмпр=11/11; Вмдоп=11/01;
3. Виконуємо послідовність дій над числами за методом алгоритму з відновленням залишку (таблиця 14.1).
Примітка: ДСДК не використовує перенос ПSg1 при переповненні суматора старшого розряду знака (див. рис. 8.1).
Відповідь: Спр=11/01101 (-13).
У таблиці 14.1 вертикальними стрілками показані знесення наступних розрядів діленого в проміжні залишки. Горизонтальні стрілки відображають розряди запису результату в регістр частки РгС. Одиниці переповнення, що одержані після підсумовування, пропадають, тому що використається ДСДК. При виконанні операції лівого зсуву залишків, переноситься вправо крапка, що відокремлює знак числа( при цьому, старший розряд знака суматора Sg пропадає).
Таблиця 14.1 - Приклад ділення чисел А на В з відновленням залишку
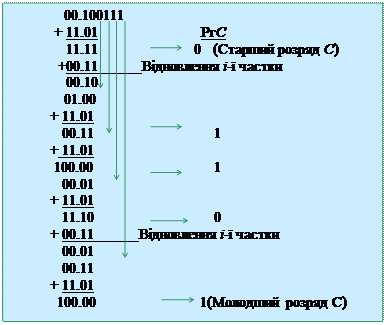 |
Відповідь: Спр=11/01101 (-13).
15 ДІЛЕННЯ ЧИСЕЛ З ФІКСОВАНОЮ КОМОЮ БЕЗ ВІДНОВЛЕННЯ ЗАЛИШКУ
Аналізуючи попередній алгоритм, бачимо, що у випадку, коли Ci - чергова цифра частки дорівнює "0", то проводиться відновлення залишку по формулі Ai-1 = Ai + В×2-i (на і-му кроці алгоритм ділення Ai = Ai-1 - В×2-i, де Ai-1 - попередній залишок, Ai - поточний залишок). Відновлений залишок приймається за A’i і процес ділення триває, тобто:
Аi+1=А’i - B×2-(i+1) =(Ai+В×2-i)-B×2-(i+1)
Перетворюючи цей вираз, одержимо:
Aі+1=Ai+B×2-(i+ 1) . (15.1)
З формули 15.1 витікає, що відновлювати залишок немає необхідності. Це дає можливість одержати інший метод ділення бінарних чисел, що і розглядається далі.
15.1 Алгоритм ділення без відновлення залишку
Метод ділення бінарних чисел без відновлення проміжних залишків виконується в послідовності:
- визначити знак частки за формулою: SgС=SgАÅSgВ;
- представити числа (операнди) у доповняльному коді в машинному зображенні, ділене (завжди), незалежно від його знака, береться в прямому коді з позитивним знаком, а дільник (завжди), незалежно від його знака, береться в доповняльному коді з негативним знаком;
- привласнити суматору значення См:=Амдоп ; РгВ:=Bмдoп; РгС:=0;
- усунути дробову частину в дільнику, переносячи кому вправо на n розрядів (за аналогією з десятковою системою числення) і, щоб дріб не змінився, у діленому також перенести вправо кому на n розрядів;
- починаючи зі старших розрядів, до діленого додають дільник у доповняльному коді, що рівнозначно вирахуванню з діленого дільника й аналізують знак проміжного залишку:
1) якщо знак проміжного залишку 00 (позитивний), то в регістр частки РгС записується 1, починаючи зі старшого розряду. Залишок зсувається на один розряд вліво (знакову крапку перенести вправо на один розряд), зноситься наступний розряд діленого, що не брав участі до цього в діленні. Після цього, проміжний залишок підготовлений до наступного додатка діленого у доповняльному коді;
2) якщо знак проміжного залишку 11 (негативний), то в регістр частки РгС записується 0, починаючи зі старшого розряду. Залишок зсувається на один розряд вліво (знакову крапку перенести вправо на один розряд), зноситься наступний розряд діленого, що не брав участі до цього в діленні. Після цього, проміжний залишок підготовлений до наступного додавання до нього дільника в прямому коді зі знаком 00;
- дії попереднього пункту повторюються до одержання машинного нуля або заданої точності обчислення (кількість розрядів дробу після коми цілої частини числа). Кома дробу встановлюється в частці після зносу останнього розряду цілої частини діленого.
- знак результату привласнюється відповідно до пункту 1. Результат ділення представлений у регістрі частки в прямому коді.
Приклад 1. Розділити на ДСДК числа (ФФЗ): А=16,25(10); В=-3,25(10)
Рішення: виконуємо ділення методом без відновлення залишку.
- визначаємо знак частки С: Sg0С=0 Å 1=1. У старші розряди регістра частки С заносимо значення негативного знака 11/;
- встановлюємо регістри РгА, РгВ і См у нульовий стан, очистивши їх від попередньої інформації;
- переводимо десяткові числа в бінарні, прямі і доповняльні коди (п.15.1):
Апр=0010000,01 (+16,25); Впр=1111,01 (-3,25); Вмдоп=11�0,11; Впр.від.=0011,01. Для вирахування використаємо Вмдоп=11�0,11. Для дільника в прямому коді зі знаком «+» беремо Вмпр=0011,01. (Щоб провести ділення з операндами А і В, як з цілими числами, перенесемо зап`яту на два розряди вліво в А і В).
Для порівняння кількості кроків при виконанні операції ділення проведіть самостійно операцію ділення на ДСДК вказаних чисел А= +16,25(10) і В= -3,25(10) за алгоритмом без відновлення залишку.
 |
Рішення наведене по алгоритму без відновленням залишку.
15.2 Ділення чисел з рухомою комою
При діленні чисел представлених у ФРК, ділення виконують над мантиссою mС=mА/mВ, а порядки віднімаються:
РС=РА-РB (15.2)
При цьому можливі два випадки:
- мантиса |mА|≥ |mB|;
- мантиса |mА|<|mB|.
Розподіл мантис виробляється в такому ж порядку, як і у форматі з фіксованою комою. При цьому, використаються методи з відновленням і без відновлення залишку. Результату привласнюється порядок РС.
Примітка. В алгоритмах ділення застосовується правило: на першому кроці підготовки операндів А і В до ділення робиться так, щоб ½А½ завжди було менше ½В½ (тимчасово змінюючи вимогу нормалізації операнда А і, відповідно, корегуючи значення порядка Р на +1) для того, щоб при першому кроці операції ділення не було переповнення молодшого знакового розряду Sg2: порівняйте дії над нормалізованими двійковими операндами, наданими у ФРК: А=+0,101.2+1 і В=+0,101.2+1:
а) ділене Ампр=00,1010�0�1; дільник Вмпр= 00,1010�0�1; частка Смпр=01,0000�0�0- отримали ненормоване число і переповнення знакового розряду (тоді, згідно вимог g і δ, треба робити зсув на першому же кроці алгоритму ділення, що затримує процес у часі);
б) ділене Ампр=00,0101�010; дільник Вмпр=00,1010�0�1; частка Смпр= 00,1000�0�1-отримали нормоване число С автоматично без переповнення знакового розряду Sg2, бо вибрано½А½<½В, (ф-ла 15.2).
6 БІНАРНО – КОДОВАНІ ДЕСЯТКОВІ СИСТЕМИ ЧИСЛЕННЯ
16.1 Загальні вимоги до БКДС
Візьмемо будь-яке десяткове число, наприклад, 689 і представимо кожний його розряд у бінарній (двійковій) системі числення. Тоді, 689=0110.1000.1001. Якщо кожний десятковий розряд представляти бінарною тетрадою (чотири молодших розряди цілих двійкових чисел), то будь-яке десяткове число буде представлене в бінарно-кодованій десятковій системі числення (БКДС). Узагальнюючи приклад для будь-якої системи числення, можна сказати, що будь-яке число А, представлене цифрами з основою В ¹ 2k, може бути записане в бінарно-кодованій системі числення (БКС) як:
АБКС = ±Σі(Σℓdℓqℓ)×Вр-1,
де d – бінарні розряди; q – вага кожного бінарного розряду. Вираз в дужках представляє ℓ-й розряд числа А, вага якого В, у свою чергу залежить від місця розташування в числі Вр-1.
На практиці в інформаційних системах найбільш широке поши-рення одержали БКДС (основні їх типи представлені в таблиці 16.1).
Взагалі, можна знайти багато варіантів і способів кодування десяткових чисел. Однак, для того щоб у БКДС можна було виконувати арифметичні операції, ефективно проводити кодування - декодування, необхідно, щоб вони відповідали ряду основних вимог:
- одиничності, тобто кожна десяткова цифра повинна представлятися єдиною бінарною комбінацією, кодом;
- впорядкованості, тобто більшій десятковій цифрі повинна відповідати більша двійкова, що забезпечує ефективність операції порівняння чисел;
- парності, що полягає в тому, що парній (непарній) десятковій цифрі повинні відповідати парні (непарні) двійкові. Це забезпечує ефективність операцій округлення, множення, ділення;
- доповняльності - сума прямого і оберненого двійкового коду будь-якої десяткової цифри повинна рівнятися коду числа 9;
- зваженості (відповідності ваг) для двійкових і десяткових розрядів.
Таблиця 16.1 - Основні типи БКДС
| Десяткове число | ЕКВІВАЛЕНТИ ДЕСЯТКОВИХ ЦИФР У КОДАХ БКДС | ||||||||
| 8421+3 | 8-4-21 | 2 з 5 | 84-2-1 | ||||||
Перераховані обмеження дозволяють значно спростити виконання арифметичних операцій. Істотним у цьому випадку є простота подання інверсних кодів і простота виділення сигналу переносу з десяткового розряду при виконанні операції додавання.
16.2 Характеристики бінарно (двійково)-десяткових кодів
Розглянемо основні характеристики і область застосування двійково-десяткових кодів (ДДК) систем числення, наведених у таблиці 16.1.
16.2.1 Код із природними вагами 8421
У цьому коді кожна десяткова цифра представлена у звичайній бінарній системі числення. Використовується код при перекладі чисел з десяткової системи у двійкову, індикації роботи регістрів, суматорів, лі-чильників і ін. пристроїв. В арифметичних операціях застосовується рід-ко через труднощі виділення переносів і одержання доповняльності до 9.
Приклад. Записати число 765 у ДДК 8421.
Рішення. Записується кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів: 765=0111.0110.0101
16.2.2 Код 8421+3 (код з надлишком 3)
У цьому коді до кожної десяткової цифри додається 3. Код не відповідає вимозі виваженості. Застосовують його найчастіше в десятковій арифметиці, тому що легко виділяється десятковий перенос.
Приклад. Записати число 765 у ДДК 8421+3.
Рішення. Записуємо кожний десятковий розряд числа 765 у двійковому коді з урахуванням вагових розрядів і надлишком +3: 765=1010.1001.1000
– Конец работы –
Эта тема принадлежит разделу:
ПРИКЛАДНА ТЕОРІЯ ЦИФРОВИХ АВТОМАТІВ
Запорізький національний технічний університет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Множення чисел на ДСОК при негативному множнику
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов