Понятие генеральной совокупности и выборки. Эмпирические аналоги параметров генеральной совокупности
Понятие генеральной совокупности и выборки. Эмпирические аналоги параметров генеральной совокупности. Два взгляда на выборку. Вероятностные свойства выборочных характеристик.
Генеральной совокупностью называют исходное множетсво объектов из которого производится выборка.
Выборка (выборочная совокупность) – совокупность случайно отобранных из генеральной совокупности объектов. Выборка должна быть репрезентативной, то есть правильно отражать пропорции генеральной совокупности, что достигается случайностью отбора, когда каждый элемент попадает в выборку.
Выборка называется повторной, если случайно отобранный для обследования объект возвращается в генеральную совокупность перед отбором следующего объекта. В противном случае выборка называется бесповторной.
Распределениеслучайной величины Х в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением.
Эмпирическим распределением называется распределение, которое каждому элементу выборки1 х1,…,хn ставит в соответствие вероятность1/n.
| Оцениваемый параметр генеральной совокупности | Точечная оценка параметра по выборке объема n | ||||||
По несгруппированным данным
(n мало)
n - объём выборки |
По сгруппированным данным
mi – частота встречаемости значения признака xi; - объём выборки Генеральная средняя или математическое ожидание µ Средняя…Теорема 1.
Рассмотрим понятие производящей функции СВ X, которая является функцией от t вида X € N(μ;σ), Из теоремы единственности следует, что каждому закону распределения… Производящая функция нормальной СВТеорема №7
Доказательство:Интервальные оценки для генеральной средней, полученной из нормальной совокупности, при известной и неизвестной генеральной дисперсии.
нижняя граница …Интервальные оценки для генеральной дисперсии, полученные по выборке из нормальной генеральной совокупности.
1)Доверит.интерв.для и ,если объём выборки небольшой (n ≤ 30): Согласно стат-ке имеющей χ2 распр-е Пирсона с ν =n-1 степ.своб,для…Оценка неизвестных параметров.
Вариационным рядом называют расположенные в возрастающем порядке значение признака. Если ряд сгруппирован, то эти значения указывают вместе с… В случае дискреного ряда х - значение признака Значение признака х … При построении интервального ряда весь диапазон изменения признака R = xmax-xmin, где соответственно максимальное и…Проверка гипотез о законе распределения ген.совокупности.
Закон распределения случайной величины F(x), построенный на основе наблюдений, имеющихся в распоряжении исследователя, называется эмпирическим.… При проверке рассматриваются две гипотезы. Нулевая гипотеза Н0 утверждает, что… Критерий согласия основан на использовании различных мер расстояний между анализируемой эмпирической функцией…Критерий согласия Пирсона
Наблюдаемое значение статистики критерия рассчитывается на основе данных, представленных в виде вариационного ряда по формуле: , где mi – частота i-го значения или интервала (число наблюдений выборки, равных… pi – вероятность принятия случайной величиной i-го значения или вероятность попадания в i-й интервал;Проверка гипотез о равенстве генеральных средних двух нормальных генеральных совокупностей
Пусть X и Y нормальные совокупности с известными дисперсиями и и неизвестными математическими ожиданиями и . Из генеральных совокупностей взяты две… Которая при выполнении нулевой гипотезы имеет нормированный нормальный закон распределения.Проблема Беренса - Фишера. Сравнение математических ожиданий двух нормальных генеральных совокупностей, генеральные дисперсии которых неизвестны и не равны.
Для справки: Проблема Беренса-Фишера- аналитическая проблема, возникшая в связи со статистич. задачей сравнения по эмпирич. данным математич. ожиданий в двух нормальных распределениях, дисперсии к-рых неизвестны (предполагается, что отношение дисперсий также неизвестно).
Пусть X и Y нормальные совокупности с равными, но неизвестными дисперсиями 
и математическими ожиданиями 
и 
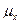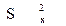. Из этих совокупностей взяты две случайные независимые выборки с параметрами
, 
и 
, 
. На уровне значимости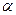 
проверяется гипотеза H0 : 
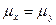. В основе критерия лежит статистика:
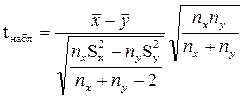
Которая при выполнении нулевой гипотезы H0 имеет распределение Стьюдента с 
степенями свободы. При заданном уровне значимости 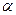выбор критической области зависит от конкурирующей гипотезы:
H1: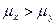 
- ПКО или H1: 
-ЛКО =>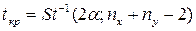 
H1: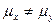 
ДКО => 
Тогда, если:
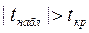=> отвергается с вероятностью ошибки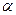
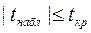=> гипотеза не противоречит опытным данным
НО! Прежде чем использовать этот критерий, нужно проверить его на применимость, проверив гипотезу о равенстве дисперсий двух генеральных совокупностей.
Пусть Х и У – генеральные совокупности, значения признаков которых распределены по нормальному закону с дисперсиями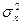 
и 
. И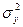з этих совокупностей взяты две случайные независимые выборки, объемами nx и ny , и пусть 
и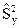 
- исправленные выборочные дисперсии,
причем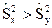 
, где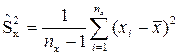 
Требуется проверить H0 :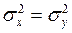 
против альтернативной H1 : 
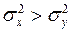. Основой критерия является статистика: 
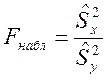, которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора(F-распределение) с 
и 
степенями свободы.
Для проверки выбирают ПКО. Границу критической области определяют из условия:
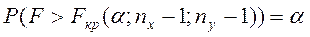
Если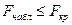 
=> гипотеза не противоречит опытным данным
Если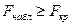 
=> гипотеза отвергается
22 Проверка предположения, что две выборки объемом n1 и n2 взяты из одной нормальной генеральной совокупности.
23 Проверка гипотез о значении дисперсии генеральной совокупности. Вычисление мощности критерия
Пусть из генеральной совокупности, значения признака которой распределены по НЗР с неизвестной дисперсией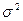 
, взята случайная выборка из n независимых наблюдений и пусть S2 – выборочная дисперсия. Требуется проверить нулевую гипотезу H0 :
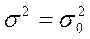, где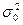 
- определенное заданное значение дисперсии. Используют выборочную характеристику: 
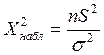, которая при выполнении гипотезы H0 имеет распределение «хи-квадрат» с (n-1) степенями свободы.
Критические области выбираются исходя из конкурирующей гипотезы:
H1: 
- ПКО => 
>
Если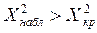 
, то нулевую гипотезу отвергают. Если 
, то гипотеза не противоречит опытным данным.
Мощность критерия в этом случае: 
H1: 
- ЛКО =>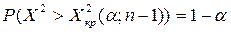 
Если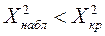 
, то гипотеза отвергается. Если 
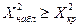- не отвергается.
Мощность критерия: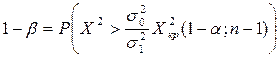 
H1: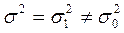 
=> ДКО => Левую и правую границы критической области находят из услови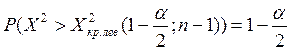й: 
и 
Если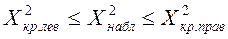 
=> гипотеза не отвергается
Есл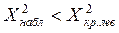и 
и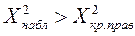 
=> отвергается
24 Проверка гипотез об однородности дисперсий ряда генеральных совокупностей. Критерии Бартлетта и Кохрана