Колебательное звено.

ξ – параметр затухания колебаний, лежит в пределах: 0 < ξ < 1

Чем меньше ξ, тем выше колебательность системы.

Временные характеристики представляют собой затухающие колебания.

 

[Закладка 2]

 

Преобразование	Исходная схема	Эквивалентная схема
1. Перенос узла ветвления через звено. а) по направлению передачи сигнала

 

Колебательное звено АФЧХ

 

 

I_M

 

 

ω=∞ ω=0

 

 

ω

 

АЧХ

 

А(ω) ξ = 0,1

ξ = 0,3

ξ = 0,4

 

ξ = 0,5

 

ξ = 0,8

 

 

ω

 

ω_p

 

Колебательное звено характеризуется наличием резонансной частоты, однако, резонансная частота, явно присутствует только для малых коэффициентов затухания.

 

ФЧХ

ω

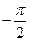ξ = 0,9

 

π

 

ξ = 0,1

φ(ω)

 

ЛАЧХ

 

L(ω) ξ = 0,1

 

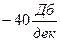
ω_ср ξ = 0,9

ω

ω_с=

 

 

Реальная ЛАЧХ может резко отличаться от асимптотической, т.е. ошибка будет более 3 Дб в зависимости от величины коэффициента затухания. В пределах от 0,4 до 0,7 можно пользоваться асимптотической ЛАЧХ.

Для других значений необходимо проводить уточнение в окрестностях ω_с (частоты сопряжения) Описываются устройства с пружинами, маятниками, катушками индуктивности и т.д.

 

Консервативное звено (частный случай колебательного звена, когда ξ = 0):

Передаточная функция:

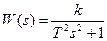
АФЧХ

I_m

 

 

ω

 

k Re

 

ω = 0

 

ω = ∞

 

 

АЧХ

 

A(ω)

 

k

 

 

ω_р ω

 

ФЧХ

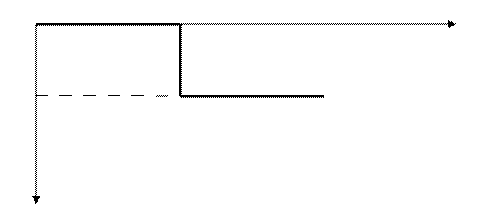
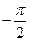ω

 

 

-π

 

φ(ω)
у консервативного звена ω_рез = ω_{сопряжения}

Переходной процесс для единичного ступенчатого сигнала и дельта функции представляет собой не затухающие колебания, равные частоте собственной колебаний системы.

 

ЛАЧХ

 

L(ω)

ξ = 0,1

 

 

 

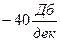
ω

 

При анализе СУ часто выделяют специальные звенья, которые не являются элементарными, но позволяют упростить анализ системы:

1) форсирующее звено первого порядка

, где τ – постоянная дифференцирования.

АФЧХ

Переходная и импульсная функции

,

Группа инерционных звеньев

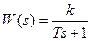
Звенья похожи, как зеркальные.

 

ЛАЧХ

L(ω)

 

 

ω

 

 

Т.е. форсирующее звено – это опережение сигнала, усиление.

 

2) Форсирующее звено второго порядка

 

 

φ(ω)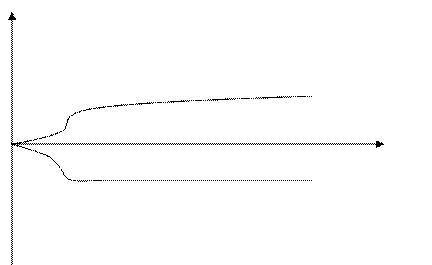

 

 

 

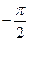ω

 

 

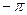
K

 

2kTξs

 

kTs kTs

 

L(ω) форсирующее звено

II порядка

 

ω

 

 

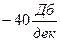
колебательное звено

 

3) Апериодическое звено второго порядка

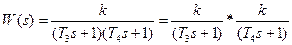
При большой дисперсии (рассеивание энергии в пространстве) энергии в объекте коэффициент затухания системы может оказаться больше единицы, и, тогда, колебательное звено, ведет себя как апериодическое звено второго порядка.

 

1)

Представляет собой интегрирующее и форсирующее звенья первого порядка

2) Интрегрально-дифференцирующее звено

Все перечисленные звенья являются алгебраическими.

 

Трансцендентные звенья. Основным и элементарным элементом этой группы является звано чистого запаздывания. Если выходная величина повторяет входную с некоторой задержкой во времени, то в идеальном случае описывается следующим образом

, где τ – время запаздывания.

Используется в любых транспортных системах.

ЛАЧХ и АЧХ такого звена совпадают с характеристиками пропорционального звена.

 

АФЧХ: ФЧХ:

I_m

 

 

Re

ωτ

 

 

φ(ω)

 

Построение АЧХ разомкнутой цепи звеньев.

Передаточную функцию можно привести к

Для построения асимптот ЛАЧХ выполняют следующие правила (правила приведены не последовательно!):

1. Частотная область разбивается на диапазоны в соответствии с уравнением . Число сопрягаемых частот равно числу постоянной времени в передаточной функции системы, поэтому число диапазонов больше на 1.

2. Низкочастотная асимптота проводится под наклоном -(20*r) Дб/дек, где r – порядок астатизма системы (число интегрирующих звеньев). Она проходит через точку с координатами ω=1 Гц, на высоте 20lgk [Дб] точка начала построения ЛАЧХ.

3. На сопрягающих частотах ω_с ЛАЧХ изменяет наклон в соответствии с тем, какому из звеньев соответствует постоянная времени сопрягающей частоты. В числителе звенья дают «+» изломы (+20Дб/дек – для форсирующего звена 1-го порядка; +40Дб/дек – для форсирующего звена 2-го порядка). Если передаточная функция в знаменателе, то наклон «-» (-20Дб/дек – для апериодического звена; -40Дб/дек – для колебательного звена).

4. Каждая новая асимптота идет до следующей сопрягающей частоты.

 

Для построения ЛФЧХ необходимо построить ЛФЧХ каждого из звеньев входящих в исходную передаточную функцию, а затем провести графическое сложение.

Сначала производится расчет максимального сдвига фаз в системе. Для этого все сдвиги фаз звеньев складывают, при этом звенья в числителе дают положительные сдвиги фаз, а в знаменателе – отрицательные. Перегиб равен

 

 

Неминимально-фазовые звенья.

Все рассмотренные ранее звенья являются минимально фазовыми, кроме звена частого запаздывания. Неминимально-фазовые звенья, это такие звенья, которые, в отличие от обычных типовых звеньев, имеют большие фазовые сдвиги при равенстве АЧХ соответствующего им звена.

 

Звено с положительным полюсом.

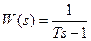(неустойчивое апериодическое звено)

АЧХ и ЛАЧХ такого звена только совпадают с АЧХ и ЛАЧХ апериодического звена

 

 

A(ω) L(ω)

 

 

 

 

ω

 

 

ω = 0 ω = ∞

Re

 

 

 

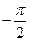
-π

 

Звено с положительным нулем

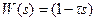
Существует также неустойчивое колебательное звено, которое так же содержит отрицательные слагаемые в знаменателе, и в отличии от колебательного звена на низких частотах имеет сдвиг фаз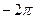

 

Закон регулирования

Под законами регулирования или управления понимают алгоритм или функциональную зависимость, определяющая управляющее воздействие на объект. Чаще всего управляющее воздействие обозначается как u(t)

Линейный закон описывается следующее формулой:

отсюда, т.к. данный закон есть сумма элементарных звеньев, то законы управления или регулирования описывают чувствительность регулятора пропорциональной, интегральной или дифференциальной составляющей.

Выделяют следующие регуляторы или законы управления (любой закон реализуется при помощи подключенных соответствующих элементарных звеньев):

P – пропорциональный закон

I – интегральный закон

PI – изодромный закон

PD – пропорционально-дифференциальный закон

И более сложные PID, PIID, PIDD и т.д.

Самые распространенные это PID регуляторы.

 

Анализ САУ

Анализ включает в себя определение способности системы эффективно функционировать и выполнять требования, предъявляемые к этой системе (быстродействие, колебательность и т.д.)

Способность функционировать оценивается по понятию устойчивости, для чего применяются критерии устойчивости. На первом этапе оценивается устойчивость линейной системы. Если система оказывается на границе устойчивости, то необходимо обязательно учесть нелинейность системы и после чего сделать вывод об устойчивости системы. Для нелинейных систем, оценка устойчивости проводится в большом и малом. Линейные системы оцениваются по устойчивости только в малом, т.е. при малых входных воздействиях.

 

Понятие устойчивости.

Устойчивость – свойство системы, характеризующее способность системы возвращаться в равновесное состояние после снятия внешних сил, которые вывели ее из данного состояния равновесия.

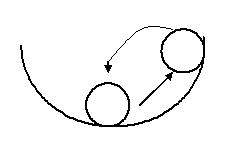устойчивая система

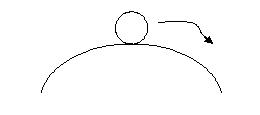неустойчивая система

 

безразличная система

А В

А В

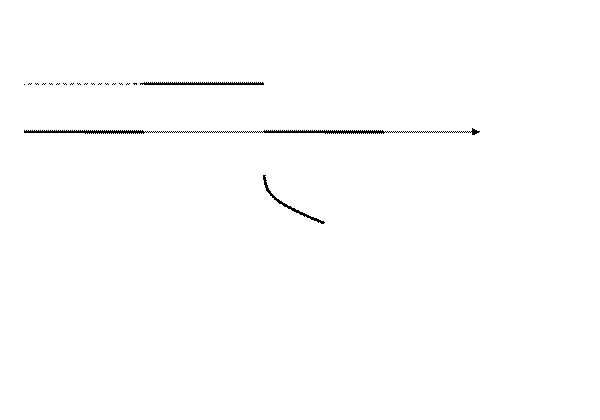
устойчивость в малом, неустойчивость в большом

 

 

 

u(t)

 

u₂

 

 

u₁

t₁ t₂ t

 

I

 

t

∞

II

 

 

t

 

III

 

 

t₁ t₂ t

 

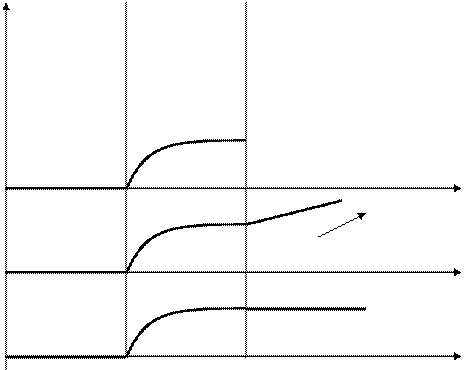
I – устойчивая система, в момент времени t₂ переходной процесс может еще не закончится

II – неустойчивая система, переходной процесс как-то продолжается

III – безразличная система, положение равновесия (на границе устойчивости)

Графики могут быть и колебательные.

 

Математическое условие устойчивости.

Т.к. по графику переходного процесса можно однозначно провести оценку устойчивости системы, следовательно необходимо найти выходной сигнал системы, который определяется из дифференциального уравнения САУ:

 

Решение данного уравнения дает нам слагаемые (У_в и У_п)

У_в – вынужденная составляющая выходного сигнала.

У_п – переходная составляющая выходного сигнала.

При чем У_п определяет поведение системы после снятия нагрузки (или сил), следовательно, зная У_п можно определить устойчивость системы, при этом У_п полностью определяется полиномом D(p), который равен:

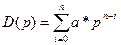
а этот полином определяет вид знаменателя передаточной функции (по нему можно определить устойчивость системы). Решение данного полинома в общем виде:

, где s₁–s_n – корни данного полинома, они же корни характеристики этого уравнения, т.е. корни знаменателя передаточной функции С₁-C_n – постоянные интегрирования.

Допустим, что у нас уравнение первого порядка, при чем корень вещественный, возможно, что отрицательный или положительный.

 

 

 

Неустойчивый

C₁e^s1t

 

 

 

Устойчивый

 

 

Если система II-го порядка, то в ней возможно появление комплексных сопряженных корней (возможны три случая):

1) корни содержат отрицательную вещественную часть В этом случае график представляет собой затухающие колебания (т.е. устойчивая система);

2) если корень с положительной вещественной частью, то получим расходящиеся колебания, т.е. система неустойчивая;

3) корни имеют нулевую вещественную часть (получим затухающие колебания), т.е. безразличную систему (система находится на границе устойчивости)

 

Для систем любого порядка, в которых корни могут быть комбинацией предыдущих случаев оказывается, что даже одна положительная вещественная часть какого-либо корня приводит к неустойчивому переходному процессу.

 

Математическое условие устойчивости:

Для устойчивости системы необходимо и достаточно, чтобы вещественная часть всех корней характеристического уравнения была отрицательна, если имеется хотя бы один корень с положительной вещественной частью, то система неустойчива.

 

 

 

I_m

+jB₂

 

+jB₃

-α₃ -α₂

Re Устойчивая система

α₁

-jB₃

 

 

-jB₂

 

 

 

 

I_m

 

+jB₂

 

-α₂

Неустойчивая система

+α₄ Re

 

-jB₂

 

Если в системе имеется хотя бы один нулевой корень (s = 0)? То система находится на апериодической границе устойчивости. Если есть хотя бы одна пара чисто мнимых корней, т.е. 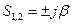(α = 0) то система находится на колебательной границе устойчивости. Для таких систем ничего нельзя сказать об устойчивости, поскольку математическая модель и математическое описание для линейных систем имеет ряд упрощений и допущений.

Т.к. нахождение корней характеристического уравнения высокого порядка является затруднительным (все математические пакеты позволяют найти корни только приблизительными методами, следовательно не обладают 100% точностью) поэтому были разработаны специальные критерии оценки устойчивости, без нахождения корней. Существует две группы критериев: 1) алгебраические; 2) частотные.

 

Алгебраические критерии устойчивости:

Не решая самого характеристического уравнения можно судить о знаках действительной или вещественной части корня по косвенным признакам. На основе этих косвенных признаков были разработаны критерии устойчивости Гурвица.

Для данного критерия составляется некий ряд неравенств, которые связывают коэффициенты характеристического уравнения системы:

λ – корни характеристического уравнения.

(где a₀>0)

Составим для такого полинома определитель Гурвица; он имеет n строк на n столбцов, где n – порядок уравнения.

 

Матрица (определитель)

Правила:

1) По главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a_n-1 до a₀.

2) От каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы увеличивались сверху вниз.

3) На место коэффициентов с индексами меньше нуля или больше n ставятся нули.

 

Условие устойчивости заключается в требовании положительности определители Гурвица и всех его диагональных миноров.

Критерии Гурвица:

Для устойчивости линейной САУ необходимо и достаточно, чтобы главный определитель Гурвица и все его диагональные миноры были больше нуля. Необходимым условием устойчивости является требование чтобы все коэффициенты характеристического уравнения были больше нуля.

Если a₀ = 0, то система находится на апериодической границе устойчивости.

Интегрирующее звено – больше всего изменений в САУ.

Если =0, то система находится на колебательной границе устойчивости.

Недостаток критерия – трудности расчетов для систем высокого порядка.

Поэтому были предложены критерии Льенара-Шепарда, который говорит, что для устойчивости линейных САУ необходимо и достаточно чтобы были положительными четные или нечентые миноры определителя Гурвица.

 

Критерий устойчивости Рауса.

Этот критерий предполагает использование коэффициентов характеристического уравнения по которым составляется таблица Рауса по определенному алгоритму. В первой строке записываются четные коэффициенты a_n, a_n-2, a_n-4, во второй нечентые a_n-1, a_n-3 и т.д. Для остальных строк используется следующая формула:

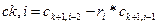
где i больше или равно s (номер строк)

k – номер столбца.

Число строк таблицы равно n+1, где n – порядок уравнения.

 

Критерий Рауса.

Для устойчивости линейной САУ необходимо и достаточно чтобы коэффициент первого столбца таблицы Рауса (c₁₁, c₁₂, c₁₃ …) были положительны. Если есть хотя бы один отрицательный, то система неустойчива. Количество переменных знаков в первом столбце определяет число первых корней.

 

Частотные критерии устойчивости.

Данные критерии относятся к графическо-аналитическим методам и по виду частотных характеристик позволяет судить об устойчивости.

Достоинства: простота построения для систем любого порядка, наглядность, возможность оценивать устойчивость замкнутых систем по частотным характеристикам разомкнутой системы.

Недостатки: неточность (приблизительность) графиков.

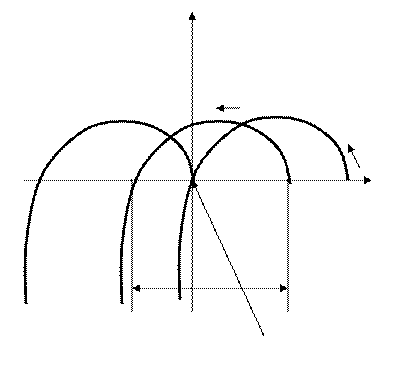
Запишем характеристический полином САУ в виде

Для такого уравнения можно применить принцип аргумента, который основан на понятии поворота векторов корней уравнения при изменении частоты ω

 

 

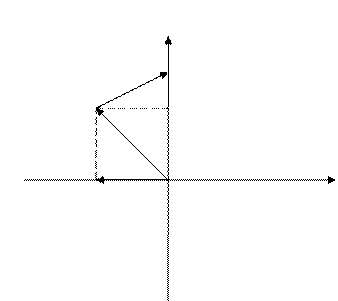
I_m

λ-λ₁

 

 

jβ

λ₁

- частота, т.е. вектор вращается

 

α Re

 

Представим характеристическое уравнение системы разомкнутой по теореме Безу. Получим:

, где (i = 1,2,3…n) – нули или корни полинома Q(A)

Если частота ω изменяется, то вектор 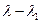или вращается по часовой или против часовой стрелки в зависимости от того с какой стороны от мнимой оси он расположен.

Для системы любого порядка необходимо оценить не только направление вращения результативного вектора (вектор вращается против часовой стрелки, если корень левый и по часовой если корень правый) для определения угла поворота необходимо сделать следующее

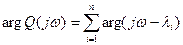
Если l нулей (корней) полинома Q(λ) расположен в правой полуплоскости а остальные (n-l) нулей, в левой то при изменении частоты ω от 0 до +∞ аргумент вектора изменится на угол (n-2l)или

 

Критерий устойчивости Михайлова

Основан на исследовании связи между расположением корней характеристического уравнения и годографом данного полинома на комплексной плоскости. Для исследования берется знаменатель передаточной функции, для которого строится частотная характеристика, которая называется годографом Михайлова.

Для устойчивости системы n-ого порядка необходимо и достаточно чтобы вектор годографа Михайлова при изменении частоты от 0 до +∞ повернулся бы против часовой стрелки не обращаясь в ноль, вокруг начала координат на угол , где n – порядок уравнения.

 

I_m

n=2

 

n=5

 

0 Re

 

n=3

 

 

n=4

 

I_m

 

0 Re

n=3

 

 

n=3

 

 

-∞

 

 

S=jω

Если =0, то годограф из начала координат и находится на границе устойчивости. Значит в системе интегрирующее звено (ошибка стремится к нулю)

 

 

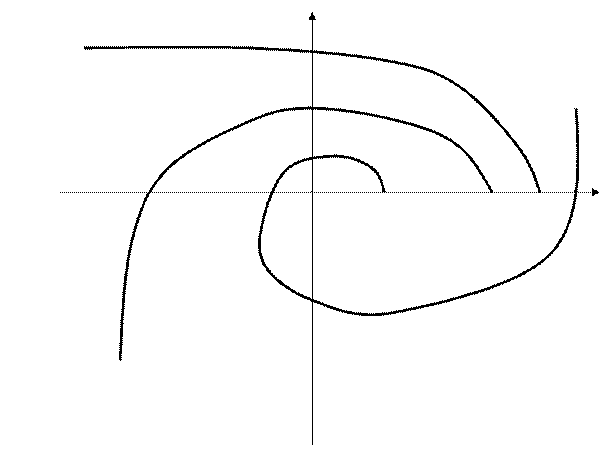
I_m

 

 

2 1 ω 3

 

a₀=k_кр

 

a₀ Re

 

k_кр

 

 

n=3 n=3 n=3 a₀=0

 

 

При 3– система на кол-ной границе устойчивости (чисто мнимый корень)

Т.к. чаще всего a₀ – коэффициент есть коэффициент усиления системы, то годограф Михайлова позволяет определить его критическое значение k_кр

Часто можно определить устойчивость системы без построения графика, для этого используется условие премежаемости корней.

 

I_m

ω₁

 

 

ω₂ ω₀ Re

 

ω₃

 

n=4

 

Из вещественной части уравнения находят частоты, при которых годограф пересекает мнимую ось U(ω)=0, эти частоты находят как корни уравнения им присваивают нечетные индексы (ω₁, ω₃, ω₅ и т.д.) аналогично для мнимого уравнения по частотам дают частные индексы (ω₀, ω₂, ω₄ и т.д.) Если выполняется условие ω₀<ω₁<ω₂< ω₃<… то условие выполнено и система является устойчивой.

 

Критерий устойчивости Найквиста (для разомкнутой системы)

Данный критерий позволяет оценивать устойчивость замкнутой системы ( с учетом обратной связи) по передаточным функциям разомкнутой системы которая в большинстве случаев проще замкнутой. Как и в случае с Михайловым так же рассматривается угол поворота некого вектора на комплексной плоскости который зависит от корней.

 

 

Замкнутая система:

 

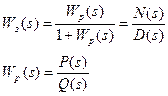
В результате такой подстановки можно убедиться что порядок заменяемой замкнутой системы совпадает с порядком разомкнутой системы, но отличается по коэффициентам. Если для такой системы определить угол поворота по принципу аргумента, то окажется что он также зависит от количества левых и правых корней в системе. При этом возможны два случая: 1- разомкнутая система устойчива; 2- разомкнутая система неустойчива, при этом замкнутая система может быть как устойчива так и неустойчива. Годограф по которому определяется вращение – годограф Найквиста, который можно найти из следующего уравнения

если s = jω, то

где - годограф Найквиста, а - АФЧХ разомкнутой системы

Т.к. один годограф от другого отличается на 1, то рассмотрим АФЧХ разомкнутой системы относительно точки с координатами (-1;j₀) (-1;0)

Если разомкнутая система устойчива, то для устойчивой разомкнутой системы необходимо и достаточно чтобы АФЧХ разомкнутой системы не охватывало точку с координатой (-1;j₀)

 

I_m I_m

 

 

ω=0 ω=0

-1 -1

 

Re Re

 

устойчивая разомкнутая неустойчивая

неустойчивая замкнутая разомкнутая система

устойчивая замкнутая

II случай – если разомкнутая система неустойчива, то для устойчивой замкнутой системы необходимо и достаточно чтобы АФЧХ разомкнутой системы охватывало точку (-1;j₀) l/2 раз, где l – число правых корней характеристического уравнения.

 

Если АФЧХ системы проходит через точку (-1;y₀), то система находится на границе устойчивости.

 

-1 ω

 

 

Логарифмический критерий Найквиста

Как и для способа определения устойчивости по АФЧХ разомкнутой системы можно оценить устойчивость и по другим частотным характеристикам разомкнутой системы. Наиболее удобные – логарифмические.

 

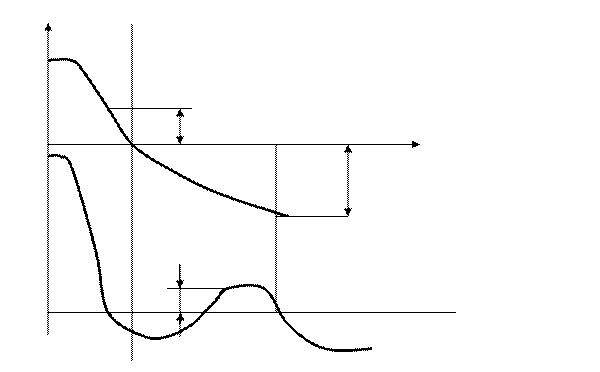
L(ω)

 

 

L(ω)<0

L(ω)>0

ω_ср L_π2 ω

 

 

L_π1

 

θ₀

-π

1 2 3

φ (ω) «-» «+» «-»

 

H_π2 H_π1 I_m

 

 

R=1

 

2 (-1)

 

3 180⁰ Re

θ₀

ω

 

 

Если рассмотреть АФЧХ и ЛЧХ, то можно увидеть четкое соответствие. Так на отрицательном направлении вещественной оси, там, где находится точка (-1;y₀) можно найти точки пересечения графика с этой осью при этом оказывается, что годограф на этих точках получает поворот -180⁰. Следовательно, эти точки на ЛФЧХ находятся на том же угле. Т.к. точка (-1;y₀) годограф может охватывать только при условии, что он >1, то на ЛАЧХ нас интересует диапазон частот, где l(ω)>0. На частоте среза (ω_ср) вектор единичен, но именно на ней по ЛФЧХ определяется степень удаленности его от линии –π

Формулировка критерия Найквиста: Для устойчивости линейной САУ необходимо и достаточно, чтобы ЛФЧХ на диапазоне где L(ω)>0 имела нулевое число переходов через именно –π

Критерий Найквиста, кроме оценки устойчивости позволяет определить так называемый закон устойчивости – на сколько обеспечена устойчивость системы, при возможных изменениях ее свойств. Выделяют два запаса устойчивости: 1) запас устойчивости по фазе; 2) запас устойчивости по амплитуде.

По фазе определяется величина угла на частоте среза (ω_ср) как разница угла –π и значения ЛФЧХ на этой частоте. Запас по амплитуде определяется по частоте на которой ЛФЧХ имеет сдвиг фазы –π, а величина ЛАЧХ на этой частоте дает запас по амплитуде. Если ЛФЧХ на частоте срезу имеет сдвиг фазы –π, то система находится на границе устойчивости.

Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо чтобы ЛФЧХ пересекло линию -πраз. Где L – число правых корней характеристического уравнения.

 

 

Устойчивая астатическая система.

 

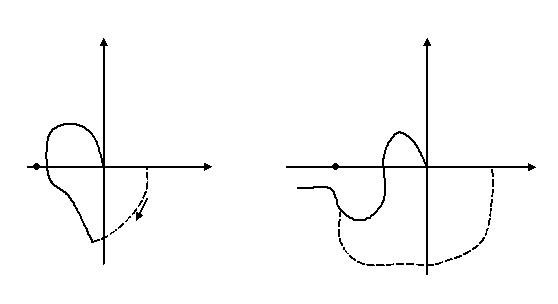
I_m I_m

 

ω=∞ ω=∞

-1 -1

0 Re 0 Re

 

первый порядок астатизма второй порядок астатизма

На данных рисунках разомкнутая система находится на границе устойчивости, но т.к. точка (-1;j₀) не охвачена, то замкнутая система устойчива.

 

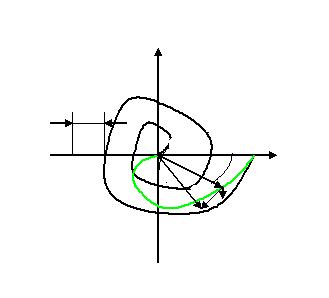
Критерий Найквиста для систем с запаздыванием.

Рассмотрим апериодическое звано II порядка

Построив для нее АФЧХ можно убедиться, что система является устойчивой для любых T, если ввести в систему звено чистого запаздывания, то АФЧХ разомкнутой системы будет определяться по следующему уравнению:

Т.е. новая характеристика будет отличаться от первоначальной только сдвигом фаз на каждой частоте. Он будет увеличиваться на величину –ωt, где t – время запаздывания.

 

 

 

 

H_π

φ(ω)

 

Из-за значений увеличивается отставание по фазе. Такое звено резко ухудшает устойчивость системы и значения уменьшает запас. При наличии такого звена всегда требуется определить приблизительное время запаздывания.

 

Области устойчивости

D – разбиение.

При анализе системы часто стоит вопрос не только оценить устойчивость системы при определенных ее характеристиках, но и найти некие границы, в которых могут измениться эти параметры без потери устойчивости системы. Наиболее просто из них способ – способ определения параметров, при которых система будет находится на границе устойчивости. Чаще всего для этого используют алгебраические критерии устойчивости.

Однако, найденные границы никаким образом не позволяют дать оценку по качеству, т.е. при каких значениях система более устойчива, при каких менее, т.е. либо устойчива либо нет. Некоторую качественную оценку дает критерий Найквиста, при помощи запаса устойчивости. Выделяют два способа определения границы устойчивости: 1) в плоскости одного параметра; 2) в плоскости двух параметров. Эти два способа позволяют определить не только границы устойчивости, но и области параметров, при которых система является устойчивой. Такие области называют областями устойчивости.

Корни, при изменении параметров каким-то образом, двигаются на комплексные плоскости и могут попасть на мнимую ось, что и будет соответствовать выходу на соответствующую границу устойчивости. В этом случае сама мнимая ось является границей области устойчивости движения корней. Если для построения областей устойчивости применить критерий Михайлова, в котором один иди два параметра могут быть заданы как варьируемые, то полученный новый годограф, будет представлять некую область устойчивости, а весь метод называется D-разбиением.

Для такого D-разбиения необходимо получить передаточные функции замкнутой системы, в который входит варьируемый параметр. После разбиения на вещественную и мнимую составляющие системы, мы получим систему из двух уравнений, из которых мы и находим области устойчивости при изменении частоты от -∞ до +∞.

 

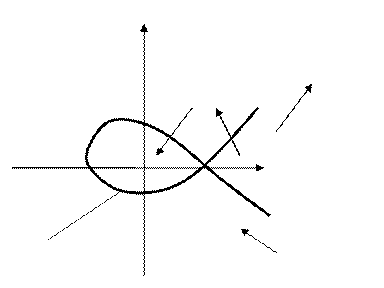
I_m(B)

 

ω = +∞

 

II

 

 

I III

 

Re(A)

 

т.е. мнимая ось ω = +∞

изогнутая

область

 

область III – область устойчивости в данном случае.

Количество правых корней равно количеству областей (+1)

В результате получаются от двух и более областей.

Далее необходимо определить какая из областей является областью устойчивости. Для этого в случае построения в плоскости первого параметра необходимо взять любую точку внутри интегрирующей области и по значениям этой точки провести оценку устойчивости по любому известному критерию. Если для данной точки система оказывается устойчивой, то в этой области по ее границе наносится штриховка внутрь с продолжением ее в другой области.

В случае построения области устойчивости в плоскости 2-х параметров нанося штриховку по следующему принципу:

Если при возрастании частоты будет положителен определитель

то штриховку наносят слева, если отрицателен – справа.

 

Структурная устойчивость САУ

Если устойчивость системы может быть достигнута путем изменения ее параметров не меняя ее структуры – такая система называется структурно устойчивой, в противном случае структурно неустойчивой. В случае отсутствия скрещивающихся связей при последовательном соедини различного набора элементарных звеньев (если интегрирующее звено только одно), то такая система может быть структурно устойчивой. Если же интегрирующих звеньев два и более, то добиться устойчивости такой системы без изменения ее структуры невозможно.

Случай многоконтурной системы управления. Удобным является провести оценку устойчивости по всем контурам по отдельности. И если каждый из них оказывается устойчивым, то такая система является так же устойчивой.

 

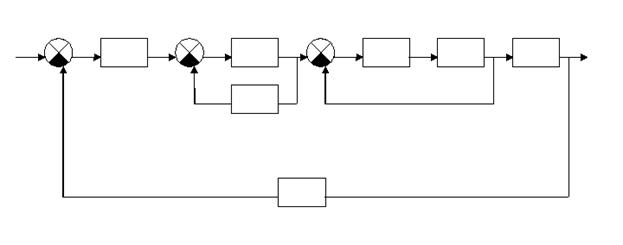
1 2 4 5 6

 

 

 

 

 

I контур содержит звенья 1,2,4,5,6,7

II контур содержит 2,3 звенья

III контур содержит 4,5 звенья

Контур содержит обратную связь и элемент сравнения.

Достоинства такого метода:

Возможность определения того контура, который оказывает отрицательное влияние на устойчивость системы и в дальнейшем нужно обеспечить устойчивость данного контура. Для таких систем можно применять все известные критерии, при этом в случае применения частотных критериев результатом будет серия частотных критериев.