Первісні поняття. Подія

Теорія ймовірностей вивчає математичну модель випробування (досліду, експерименту), наслідок якого неможливо передбачити. При цьому припускається, що таке випробування може бути повторено необмежену кількість разів при незмінних основних умовах. Комплекс другорядних умов, які неможливо проконтролювати, змінюється від випробування до випробування. Саме ці умови приводять до того, що результати однотипних випробувань можуть бути різними.

Приклад 1. Підкидається монета. Результатом випробування (спостереження) є випадання монети гербом або ціною вгору.

Урахувати всі причини, що впливають на результат випробування з підкиданням монети, неможливо. Деякі з цих причин невідомі, а вплив інших (опір повітря, пружні властивості монети і поверхні, на яку вона падає, висота підйому монети, кутова швидкість і т.д.) вдається оцінити тільки приблизно. Тому неможливо точно передбачити впаде в даному випробуванні монета гербом вверх чи ні. Однак, є можливість оцінити, як часто монета, яку підкидають багато разів, впаде гербом вгору.

Позначимо через W множину наслідків випробування, що розглядається. Множина W та її різні підмножини використовуються при побудові імовірносної моделі цього випробування. Множину W називають простором елементарних подій. При цьому, кожному наслідку випробування ставиться у відповідність одна і тільки одна точка простору W – елементарна подія w. Випадкова подія (далі просто подія) – будь-який факт, який може наставати чи не наставати в результаті проведення випробування. Позначають випадкову подію, як правило, великими літерами латинського алфавіту. Для кожної випадкової події A і кожної елементарної події w можна сказати, сприяє чи ні елементарна подія w появі події A. Подію A можна розглядати як підмножину W, яка складається з тих точок w, що сприяють появі події A.

Малюнок 1.1 відповідає тому випадку, коли елементарна подія w₁ сприяє події A а елементарна подія w₂ не сприяє.

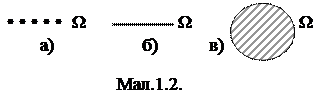Множина W може бути як дискретною (мал.1.2а), так і неперервною (мал.1.2б,в). У першому випадку вона складається із скінченної або зчисленної (такої, яку можна перерахувати) кількості точок, а у другому – із незчисленної кількості точок.

Приклад 2. Підкидається гральний кубик (кубик, зроблений з однорідного матеріалу, грані якого позначені числами 1,2,3,4,5,6). Результатом випробування (спостереження) є число, що випало на верхній грані кубика.

Простір W складається з шести точок w_i, де через w_i позначено елементарні події, що відповідають випаданню грані, на якій написано число i (i=1,2,3,4,5,6): W{w₁,w₂,w₃,w₄,w₅,w₆}. Події A (випадання парного числа) сприяють елементарні події w₂, w₄, w₆ – A{w₂,w₄,w₆}.

Приклад 3. Монета підкидається до першого випадання герба.

Простір W складається зі зчисленної кількості точок w_i, де через w_i позначено елементарну подію, що відповідає випаданню ціни (Ц) в перших i–1 підкиданнях монети і герба (Г) при i-му підкиданню. Отже, w₁ – Г, w₂ – Ц₁Г, w₃ – Ц₁Ц₂Г, ..., w_n – Ц₁Ц₂...Ц_n-1Г, ..., w_¥ – Ц₁Ц₂...Ц_n... (w_¥ - відповідає випадку, коли герб не з’являється ніколи) і W{w_¥,w₁,w₂,w₃, ...}.

Нехай подія A – це випадання герба при другому підкиданні монети, а подія B – випадання герба не раніше другого підкидання. Тоді події A сприяє лише елементарна подія w₂ – A{w₂}, а події B – елементарні події w₂, w₃, ..., w_¥ – B{w₂, w₃, ..., w_¥}.

Приклад 4. Визначається термін безвідмовної роботи приладу. Простір W складається з незчисленної множини додатних чисел (ці числа не можна перерахувати та пронумерувати).

Нехай подія A полягає в тому, що прилад працював не більше 100 годин. Тоді W{t: t>0}, а A{t: 0<t<100}.

Приклад 5. Проводиться стрільба по плоскій круглій мішені радіуса R кулею, розмірами якої можна знехтувати (кидається точка на площину).

Елементарною подією w є точка попадання в мішень (припускаємо, що непопадання умовами випробування виключається). Простір W складається з незчисленної множини точок, які неможливо пронумерувати W{ (x,y): x²+y² £ R²}, (x,y) – прямокутні координати точки попадання в системі координат, початок якої співпадає з центром мішені (мал. 1.2.в).

Нехай події A та B полягають в тому, що точка попадання знаходиться відповідно на відстані R/2 і на відстані, не меншій, ніж R/2. Тоді A{ (x,y): x²+y² = R²/4}, B{(x,y): R²/4 £ x²+y² £ R²}.

Зауваження. У зв’язку з прикладом 5 відзначимо:

1. Якщо нас цікавить тільки відстань від точки попадання до центра мішені, то доцільно ототожнити всі точки, які знаходяться на колі x²+y²=r², rÎ[0,R]. Це приводить нас до одномірного простору елементарних подій W₁{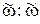Î[0,R]} , який має простішу структуру, ніж W (мал.1.2.б). Подія A співпадає з елементарною подією =R/2.

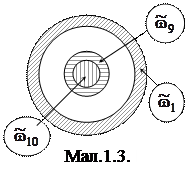
2. Нехай мішень розбита концентричними колами x²+y² = (kR/10)² (k=1,2,3...,10) на 10 зон, кожна з яких відповідає певному числу вибитих очок (мал.1.3). Усі точки, що попадають в одну зону, вважатимемо тотожними. В результаті приходимо до дискретного простору W₂{} (мал.1.2.а). Події B сприяють елементарні події , , .

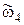Подія, що наступає при будь-якому наслідку випробування, називається вірогідною. Вона співпадає з множиною W і позначається надалі також літерою W. Подія, яка не наступає ні при жодному з наслідків випробування називається неможливою. Вона співпадає з пустою множиною і надалі позначається символом Æ. В умовах прикладу 2 випадання не більше шести очок – вірогідна подія, а випадання семи очок – неможлива.

Відзначимо, що коли дискретний простір W якогось випробування складається з n точок, то кількість всіх подій, пов’язаних з цим випробуванням дорівнює 2ⁿ.

Подія 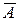, яка полягає в тому, що подія А не наступає, називається протилежною події А або запереченням А (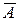доповнює множину А до W: 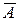=WА). В умовах прикладу 2 подія 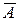{w₁,w₃,w₅}.