рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Вид работы: Конспекты
/
Умовна ймовірність

Реферат Курсовая Конспект

Выберите учебное заведение

Умовна ймовірність

Умовна ймовірність - Конспект, раздел Философия, Конспект лекцій з курсу ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА ЕЛЕМЕНТИ Нехай Атаb Є Подіями, Пов’Язаними З Деяким Випробуванням І P(B)>0. ...

Нехай АтаB є подіями, пов’язаними з деяким випробуванням і P(B)>0.

Означення 1. Умовною ймовірністю P(АïB) події А за умови здійснення події B називається відношення

. (1)

Властивості умовної ймовірності аналогічні властивостям ймовірностей 1-3 пункту 1.2.2.

Із співвідношення (1) випливає теорема множення ймовірностей

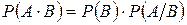. (2)

Якщо P(A)>0, то теорема множення може бути записана у вигляді

. (2¢)

Ця теорема дозволяє знайти ймовірність перерізу (добутку) подій, якщо із змісту задачі зрозумілі (легко обчислюються) значення умовних ймовірностей.

Приклад 1. Ймовірність аварії при запуску ракети дорівнює 0,15. Ймовірність аварії на старті є 0,12. Яка ймовірність аварії при умові успішного старту.

Розв’язок. Нехай подія A полягає у тому, що запуск ракети успішний, а подія B - це успішний старт ракети. Із умов задачі випливає, що A·B=A. Отже,

Таким чином, P(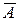/B)=1–P(A/B)=0.034.

Означення 2. Подія А називається незалежною від події B, якщо P(АïB)=P(А) (P(B)>0).

Нехай подія А незалежна від події B і P(A)>0. Тоді з формул (2) та (2¢) випливає, що подія B незалежна від події А. Таким чином, поняття незалежності подій є взаємним.

Події А та B незалежні тоді і тільки тоді, коли виконується рівність

. (3)

Якщо події А та B незалежні, то будуть незалежними такі пари подій: `А та B; А та`B;`А та`B.

У тому випадку, коли кількість подій перевищує два, вводиться поняття незалежних у сукупності подій. Останнє означає, що ймовірність якої-небуть події не залежить від здійснення інших. Наприклад, для трьох подій А₁, А₂, А₃, незалежних у сукупності, повинні виконуватись співвідношення P(A₁/A₂)=P(A₁), P(A₁/A₃)=P(A₁), P(A₁/A₂·A₃)=P(A₁), P(A₂/A₃)=P(A₂), P(A₂/A₁·A₃)=P(A₂), P(A₃/A₁·A₂)=P(A₃). Для подій А₁, А₂,..., А_n, незалежних у сукупності, справедливе співвідношення

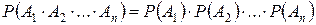. (3¢)

Приклад 2. Проводиться два постріли по мішені. Ймовірності попадання при першому та другому пострілі дорівнюють відповідно 0.3 і 0.6. Яка ймовірність, що у мішені буде: а) точно одна пробоїна; б) хоча б одна пробоїна?

Розв’язок. Позначимо через A_i (i=1,2) подію, яка полягає у тому, що при i–му пострілі буде попадання у мішень. Події A₁ та A₂ незалежні, але сумісні.

а) Нехай A – подія , яка полягає у тому, що у мішені буде точно одна пробоїна. Тоді 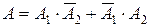. Оскільки поді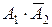ї і 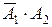несумісні, то на підставі аксіоми 3 і теореми множення ймовірностей одержимо

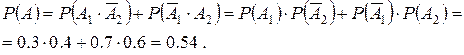
б) Нехай B – подія , яка полягає у тому, що в мішені буде хоча б одна пробоїна. Тоді B=A₁+A₂ і на підставі теорема додавання і множення ймовірностей матимемо

Інший спосіб розв’язку: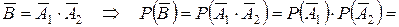

Приклад 3. Для умов прикладу 1 пункту 1.1.2 знайти ймовірність безвідмовної роботи (надійність) схеми, елементи якої виходять із ладу незалежно один від іншого з ймовірностями рівними відповідно 1– p_i (i=1,2,3). Яка схема надійніша при умові p_i=p (i=1,2,3)?

Розв’язок. Зрозуміло, що події A_i, які розглядаються в прикладі, незалежні у сукупності.

а) На підставі теорем додавання та множення ймовірностей одержимо:

P(A) =P(A₁·A₂)+P(A₃) – P(A₁·A₂·A₃)=P(A₁)·P(A₂)+P(A₃) – P(A₁)·P(A₂)·P(A₃)=

= p₁·p₂+p₃ – p₁· p₂· p₃.

б) Аналогічно знаходимо

P(A) =P(A₁)·P(A₂+A₃) =P(A₁)·[P(A₂)+P(A₃) – P(A₂)·P(A₃)] =

= p₁·(p₂+p₃ – p₂· p₃).

Більш надійною є перша схема, оскільки при p Î(0;1)

p²+p – p³> 2p² – p³.

Відмітимо, що при знаходженні ймовірності суми сумісних подій доцільно переходити до протилежної події.

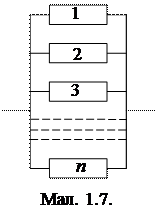
Приклад 4. Система (мал.1.7) складається з n паралельно з’єднаних елементів, які виходять з ладу протягом деякого проміжку часу незалежно один від одного з ймовірностями 1 – p_i (i=1,…,n). Знайти ймовірність безвідмовної роботи (надійність) системи.

Розв’язок. Нехай подія A_i (i=1,…,n) означає, що i-тий елемент не вийшов з ладу (справно працює). Позначимо через A подію, яка полягає у безвідмовній роботі системи. Оскільки система безвідмовно працює лише тоді, коли працює хоча б один її елемент, то A = A₁ÈA₂È...ÈA_n. Перейдемо до події, протилежної A (система виходить з ладу, якщо перестали функціонувати всі її елементи): . Оскільки події A_i незалежні у сукупності, то

P(A) = 1 – P(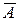) = 1 – = 1 – (1 – p₁)...(1 – p_n).

Внаслідок того, що 1 – p_i < 1, одержаний результат узгоджується з допущенням про зростання надійності системи при зростанні n.

Використаємо результат прикладу 4 для того, щоб знайти найменше число однотипних елементів, необхідних для забезпечення заданої надійності P системи:

P =1 – (1 – p)ⁿ Þ n = ëlg(1 – P) / lg(1 – p)û +1, (4)

де ëaû – найбільше ціле число, менше від a.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Конспект лекцій з курсу ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА ЕЛЕМЕНТИ

ХАРКІВСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ БУДІВНИЦТВА ТА АРХІТЕКТУРИ... Конспект лекцій з курсу...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Умовна ймовірність

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Передмова
Конспект лекцій підготовано для студентів технічних ВУЗ’ів. При його створенні ставилася задача відібрати матеріал, який можна викласти за час, відведений учбовим планом на курс теорії ймовірності

Первісні поняття. Подія
Теорія ймовірностей вивчає математичну модель випробування (досліду, експерименту), наслідок якого неможливо передбачити. При цьому припускається, що таке випробування може бути повторено необмежен

Алгебра випадкових подій.
Подія А &Egr

Частота та ймовірність випадкової події
Ймовірність події A – це число, яке характеризує можливість (долю впевненості) появи цієї події в розглядуваному випробуванні (досліді, експерименті). Іноді ймовірність того чи іншого резуль

Аксіоми ймовірності та її властивості.
Означення 1. Ймовірністю називається числова функція P(A), визначена на множині всіх подій, пов’язаних з даним експериментом, яка задовольняє таким аксіомам: 1. P(A) ³ 0; 2.

Формула повної ймовірності
Часто для вивчення випробування, з яким пов’язана подія A, корисно ввести до розгляду події Hk, дл

Класичне означення ймовірності
Розглянемо випробування, простір якого складається з N точок (випробування із скінченою кількістю наслідків). Якщо ймовірності елементарних подій відомі, то ймовірність будь-якої події A у випробув

Комбінаторні методи підрахунку кількості наслідків
Для того, щоб знайти ймовірність події за формулою (1), потрібно знати і загальну кількість наслідків випробування і число наслідків, які сприяють настанню цієї події. Суттєву роль при підрахунках

Асимптотичні формули для схеми Бернуллі.
Формула (1) приводить до громіздких обчислень при великих значеннях n і k, а також при малих значеннях p або 1– p. Тому, доцільно мати наближені, але прості формули для розрахунку відповідних ймові

Випадкова величина та її функція розподілу
Означення 1. Одновимірною випадковою величиною називається величина, значення якої залежить від наслідку експерименту (інакше кажучи, випадковою величиною називається числова функція, яка визначена

Дискретні випадкові величини
Випадкова величина X називається дискретною, якщо: 1) сукупність її можливих значень можна перерахувати – x1, x2,..., xn (або x

Неперервні випадкові величини
Випадкова величина X називається неперервною, якщо: 1) множина її значень співпадає з проміжком (кількома проміжками) числової осі; 2) ймовірність того, що випадкова величина набуває будь-як

Перетворення розподілів
Нехай розподіл випадкової величини X є відомим. Потрібно знайти розподіл випадкової величини Y, яка пов’язана з функціональною залежністю Y=g(X) (Y приймає значення g(

Функція розподілу випадкового вектора
Якщо кожний наслідок випробування задається упорядкованою сукупністю n випадкових величин, то прийнято говорити про n-вимірний випадковий вектор. Виявляється, що для повного опису ви

Дискретний випадковий вектор
Y X y1 y2 ... ym x1

Неперервний випадковий вектор
Випадковий вектор називається неперервним, якщо його координати X та Y є неперервними випадкови

Найважливіші види двовимірних розподілів.
1) Рівномірний розподіл. Випадковий вектор називається рівномірно розподіленим у області D, якщо

Закон розподілу суми випадкових величин
Теорема. Нехай випадкові величини X та Y незалежні та мають щільності ймовірностей pX(x) і pY(y). Тоді щільність ймовірності випадков

Ентропія і інформація
Нехай – випадковий вектор. Означення 1. Інформацією, яка міститься в координаті Y по відношен

Стійкість середнього арифметичного
Повну інформацію про випадкову величину дає її розподіл ймовірності. Проте часто експериментатор не володіє такою інформацією, та вона і не є необхідною. Досить охарактеризувати випадкову величину

Математичне сподівання випадкової величини
Означення 1. Математичним сподіванням випадкової величини X називається число MX, яке в залежності від типу випадкової величини визначається формулою

Математичне сподівання функції випадкової величини
Теорема 1. Якщо розподіл випадкової величини X є відомим, то математичне сподівання випадкової величини Y=g(X) дорівнює

Математичне сподівання функції випадкового вектора
Сформулюємо результат, в якому формули (1) та (2) містяться як окремі випадки. Теорема 1. Якщо відомий розподіл випадкового вектора

Кореляційний момент випадкових величин
Означення 1. Кореляційним моментом (кореляцією, коваріацією) K(X,Y) випадкових величин X та Y називається число K(X,Y)=M

Дисперсія випадкової величини та її властивості
Після того, як математичне сподівання випадкової величини знайдено, виникає питання, наскільки сильно значення випадкової величини відхиляється від математичного сподівання. Характеристикою ступен

Дисперсія суми випадкових величин
Теорема. 1) Якщо випадкові величини X та Y корельовані (отже, залежні), то D(X+Y)=DX+DY+2K(X,Y); (4) 2) Якщо випадкові вели

Нерівність П.Чебишева
Нерівність П.Чебишева встановлює верхню межу для ймовірності відхилення випадкової величини від її математичн

Коефіцієнт кореляції та кореляційна матриця
Означення 1. Коефіцієнтом кореляції rX,Y випадкових величин X та Y називається число

Регресія
Якщо ми знаємо розподіл однієї координати випадкового вектора при умові, що інша координата приймає певне значення, то можна ввести поняття умовного математичного сподівання. Означення 1.

Теорія масового обслуговування.
Ця теорія є одним з найважливіших розділів прикладної теорії ймовірності. Теорія масового обслуговування вивчає функціонування систем, у які поступають виклики (вимоги) на обслуговування. Моменти н

Найпростіші задачі теорії надійності
Головне питання теорії надійності полягає в визначенні ймовірнісних характеристик працездатності системи, якщо відома її структура і ймовірносні характеристики працездатності окремих елементів.

Таблиця 1.
Значення функції . x Ф(x

Таблиця 2.
Значення te(n-1), які задовольняють рівнянню

Таблиця 3.
Значення χk2(ε), які задовольняють рівнянню

Таблиця 4.
n ε=0.1 ε=0.05 ε=0.01 z0.1(1)(n)

Таблиця 5.
Значення Fn,m(ε), які задовольняють рівнянню , де