Неперервні випадкові величини

Випадкова величина X називається неперервною, якщо: 1) множина її значень співпадає з проміжком (кількома проміжками) числової осі; 2) ймовірність того, що випадкова величина набуває будь-якого наперед заданого значення x₀ дорівнює нулю: P{X= x₀}= 0 (взагалі кажучи, із 2) випливає 1)). Зауважимо, що хоча P{X=x₀}=0, подія X=x₀ є можливою.

Випадкові величини, описані вище у прикладах 3), 4), 5) пункту 2.1.1, є неперервними.

Означення 1. Невід’ємна функція p_X(x) називається щільністю ймовірності (щільністю розподілу) випадкової величини X, якщо ймовірність попадання випадкової величини у довільний проміжок [x₀; x₀+Dx) малої довжини приблизно дорівнює p_X (x₀)·Dx:

P{XÎ[x₀; x₀+Dx)} ~ p_X (x₀)·Dx (Dx®0). (6)

Таким чином, число p_X (x₀)·Dx характеризує долю тих випробувань у достатньо довгій серії, в яких випадкова величина X попадає у проміжок [x₀; x₀+Dx).

Щільність ймовірності p_X(x) випадкової величини X має розмірність, обернену до X.

Щільність ймовірності p_X (x) випадкової величини X має таку характерну властивість, яку сформулюємо у вигляді теореми.

Теорема. Ймовірність попадання неперервної випадкової величини X у проміжок [c; d) знаходиться за формулою

. (7)

Для доведення формули (7) потрібно розбити проміжок [c; d) на велику кількість відрізків [x_k; x_k+1) малої довжини Dx_k (відрізки не перетинаються). Ймовірність попадання випадкової величини X у проміжок [x_k; x_k+1) на підставі (6) приблизно дорівнює p_X (x_k)Dx_k. Підсумовуючи ці ймовірності і переходячи до границі при max Dx_k ® 0, одержуємо формулу (7). У лівій частині формули (7) можна замінити проміжок [c; d) на [c; d], (c; d). Геометричний зміст теореми дає малюнок 2.5.

Із співвідношення (7) випливають такі наслідки:

1) 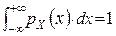(умова нормування);

2) .

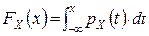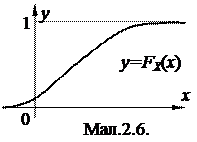Наслідок 2) у точках неперервності функції p_X (x) має таку еквівалентну форму запису:

.

Функція розподілу неперервної випадкової величини є неперервною кусково-гладкою функцією. Характерний вигляд функції розподілу приведено на мал.2.6.

Приклад 1. Щільність ймовірності неперервної випадкової величини X має вигляд

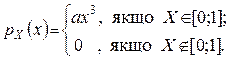
Знайти: 1) a; 2) F_X (x); 3) P{XÎ[1 ∕ 3; 4]} .

Розв’язок. 1) Коефіцієнт a знаходимо із умови нормування:

.

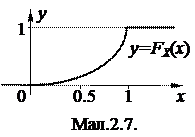
2)

Графік функції розподілу приведено на мал.2.7.

3) .

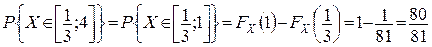Розглянемо деякі найбільш важливі неперервні розподіли.

1) Рівномірний (прямокутний) розподіл. Випадкова величина X рівномірно розподілена у проміжку [c ; d], якщо її щільність ймовірності має вигляд (мал.2.8.а):

Цей розподіл є неперервним аналогом класичного означення ймовірності (відповідає припущенню про довільний вибір точки у проміжку [c ; d]). Графік функції розподілу приведено на мал.2.8.б.

Якщо при вимірюванні результат округляється до найближчого цілого значення, то помилка вимірювання є неперервною випадковою величиною, яка рівномірно розподілена у проміжку [– 0.5 ; 0.5].

Помилка, яка допускається при округленні числа з точністю до 10^-m, рівномірно розподілена у проміжку [– 0.5·10^-m ; 0.5·10^-m].

2) Показниковий розподіл. Випадкова величина X має показниковий розподіл з параметром l>0, якщо її щільність розподілу

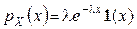, (8)

де 1(x)= – одинична функція.

Відповідна функція розподілу має вигляд

.

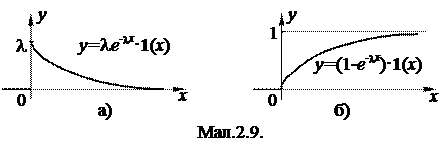
Графіки щільності ймовірності та функції розподілу приведені на мал.2.9.а і 2.9.б.

Показниковий розподіл (і тільки він серед неперервних розподілів) має властивість «відсутності післядії»:

P{X > x₁+ x₂ ⁄ X > x₁} = P{X > x₂} (x₁, x₂ > 0).

Дійсно,

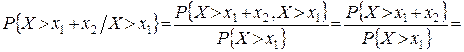
Зауваження. Нехай кількість відмов приладу на проміжку часу [0 ; t] розподілена за законом Пуассона з параметром lt:

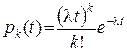
і випадкова величина T – тривалість проміжку часу між двома послідовними відмовами приладу (мал.2.10). Тоді випадкова величина T розподілена за показниковим законом з параметром l:

p_T (t) =λe^–λt ·1(t).

Дійсно,

F_T (t) =P{T< t} =1–P{T ≥ t}.

Оскільки подія T ³ t означає, що на проміжку [0 ; t] прилад працює безвідмовно, то P{T ³ t} = p₀(t) =e^–λt. Отже,

F_T (t) =1–e^–λt (t ≥0)

і, таким чином,

.

Властивість відсутності післядії приводить до того, що ймовірність безвідмовної роботи приладу протягом проміжку часу тривалістю s не залежить від того, який проміжок часу t₁ прилад уже пропрацював (мал.2.11).

Функцією надійності P(t) називається ймовірність P{T ≥ t} безвідмовної роботи приладу протягом проміжку часу t:

P(t)= P{T ≥ t}=1– P{T < t}=1–F_T (t).

Таким чином, функція надійності дорівнює P(t)=e^–λt·1(t), якщо відмови апаратури розподілені за законом Пуассона.

У деяких задачах (пов’язаних із старінням апаратури) вважають, що випадкова величина T – тривалість проміжку часу між двома послідовними відмовами приладу розподілена за законом Вейбулла-Гнеденко (при r =1 одержуємо показниковий розподіл). У цьому випадку функція надійності P(t) має вигляд:

P(t)=.

3) Нормальний (Гаусів) розподіл. Випадкова величина X має нормальний розподіл з параметрами a та s², якщо її щільність розподілу має вигляд (мал.2.12.а):

. (9)

У подальшому запис X~N(a;s²) означатиме, що випадкова величина X має розподіл Гауса з параметрами a та s². Графік розподілу Гауса є симетричним відносно прямої x=a. Єдиний максимум досягається при x=a і дорівнює . Оскільки площа під графіком дорівнює 1, то при зменшенні s графік стає більш «високим» та «вузьким».

Функція розподілу випадкової величини X~N(a;s²) виражається через функцію Лапласа Ф(x) (пункт 1.5.2). Дійсно,

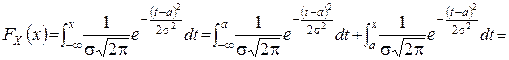
Графік функції розподілу приведено на мал.2.12.б.

Розподіл Гауса відіграє фундаментальну роль в застосуваннях теорії ймовірності.

Оскільки ймовірність попадання випадкової величини у проміжок дорівнює різниці значень функції розподілу на кінцях проміжку, то

. (10)

Якщо проміжок [c; d] довжиною 2ss розташований симетрично відносно точки x=a, то формула (10) набирає особливо простого вигляду

. (10¢)

Зокрема, ймовірність попадання у проміжок [a-3s; a+3s] дорівнює 0.9973. Таким чином, можна стверджувати, що подія {XÏ[a-3s; a+3s]} є практично неможливою. У цьому полягає знамените правило «трьох сигм».

Приклад 2. Відхилення розміру деталі від стандартного розподілено за законом N(0;16 мм²). Деталь вважається придатною, якщо відхилення від стандарту не перевищує 6мм. Який відсоток випуску непридатних деталей?

Розв’язок. Нехай випадкова величина X – відхилення розміру деталі від номінального. Знайдемо ймовірність того, що деталь буде забраковано

Таким чином, брак складає майже 13.5%.