рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Программирования.
Реферат Курсовая Конспект
Программирования.
Программирования. - раздел Философия, ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств Постановка Задачи Линейного Программирования В Общей Форме...
Постановка задачи линейного программирования в общей форме имеет вид:
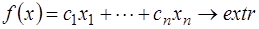 (з)
(з)
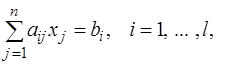
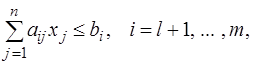
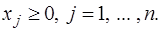
Здесь 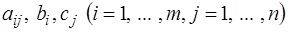 – заданные величины,
– заданные величины, 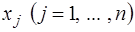 – неизвестные переменные.
– неизвестные переменные.
Задачей линейного программирования в канонической форме называется следующая задача:
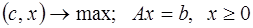 . (зк)
. (зк)
Здесь  – неизвестная переменная,
– неизвестная переменная, 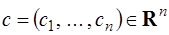 и
и 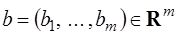 – заданные векторы,
– заданные векторы, 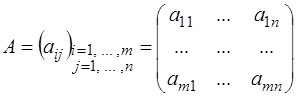 – заданная матрица размера
– заданная матрица размера  со столбцами
со столбцами 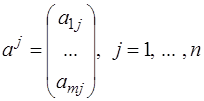 .
.
Задачей линейного программирования в нормальной форме называется следующая задача:
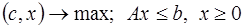 . (зн)
. (зн)
Задачи линейного программирования в различных формах можно свести друг к другу путем введения дополнительных координат, изменения матрицы 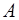 , изменения знака целевой функции
, изменения знака целевой функции 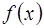 . Например, задача (зн) сводится к задаче (зк) путем введения дополнительных координат
. Например, задача (зн) сводится к задаче (зк) путем введения дополнительных координат 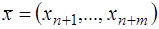 :
:
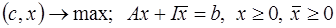 ,
,
где 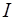 – единичная матрица размера
– единичная матрица размера 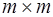 .
.
Более подробно рассмотрим задачу линейного программирования в канонической форме. Множество допустимых точек задачи (зк) имеет вид:
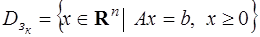
и представляет собой выпуклый многогранник в пространстве 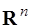 .
.
Определение. Точка 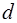 выпуклого множества
выпуклого множества 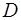 называется крайней (угловой), если не существует точек
называется крайней (угловой), если не существует точек 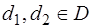 и числа
и числа 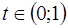 таких, что
таких, что 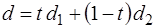 . ▲
. ▲
У многогранников крайними точками являются вершины. Поэтому, если существует экстремум линейной функции, то он достигается в крайней точке выпуклого многогранника. Число крайних точек множества 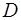 , задаваемого в виде конечного числа линейных равенств и неравенств, конечно. Таким образом, для решения задачи линейного программирования (если оно существует) достаточно перебрать значение целевой функции
, задаваемого в виде конечного числа линейных равенств и неравенств, конечно. Таким образом, для решения задачи линейного программирования (если оно существует) достаточно перебрать значение целевой функции 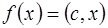 во всех крайних точках множества
во всех крайних точках множества 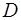 . Но нахождение всех этих крайних точек и перебор значений целевой функции в них – операция довольно трудоемкая.
. Но нахождение всех этих крайних точек и перебор значений целевой функции в них – операция довольно трудоемкая.
Симплекс‑метод решения задачи линейного программирования позволяет, начиная с некоторой исходной точки, переходить к другой по направлению наибольшего возрастания функции 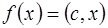 .
.
Определение. Задача (зк) называется невырожденной, если любая крайняя точка множества 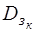 содержит ровно
содержит ровно 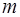 положительных координат. ▲
положительных координат. ▲
Пусть 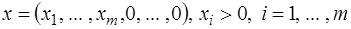 – крайняя точка в невырожденной задаче (зк). Вектор
– крайняя точка в невырожденной задаче (зк). Вектор 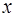 можно представить в виде
можно представить в виде 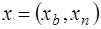 , где
, где 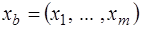 – базисный вектор,
– базисный вектор, 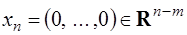 – небазисный вектор. Аналогично, матрицу
– небазисный вектор. Аналогично, матрицу 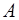 можно представить в виде
можно представить в виде 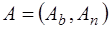 , где
, где 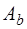 – матрица, состоящая из первых
– матрица, состоящая из первых 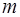 столбцов матрицы
столбцов матрицы 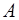 .
.
Столбцы матрицы 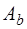 линейно независимы, т.е. матрица
линейно независимы, т.е. матрица 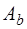 является невырожденной. Действительно, допустим противное, что столбцы
является невырожденной. Действительно, допустим противное, что столбцы 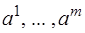 линейно зависимы. Тогда существует ненулевой набор множителей
линейно зависимы. Тогда существует ненулевой набор множителей 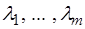 такой, что
такой, что 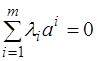 . Значит
. Значит 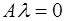 для вектора
для вектора 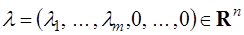 . Поэтому точка
. Поэтому точка 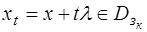 при малых
при малых  как больших нуля, так и меньших нуля. Это означает, что точка
как больших нуля, так и меньших нуля. Это означает, что точка 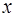 не является крайней. Получили противоречие.
не является крайней. Получили противоречие.
Правило решения задач по симплекс‑методу.
1) Привести задачу к канонической форме.
2) Найти крайнюю точку 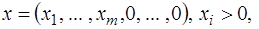
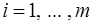 ,
, 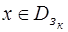 .
.
3) Построить симплексную таблицу для начальной крайней точки. В таблице 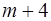 строки и
строки и 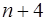 столбца. В первом столбце, начиная с 3‑его по
столбца. В первом столбце, начиная с 3‑его по 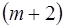 ‑ое место находятся базисные векторы
‑ое место находятся базисные векторы  , соответствующие положительным координатам начальной крайней точки
, соответствующие положительным координатам начальной крайней точки 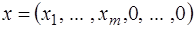 . Во втором столбце на аналогичных местах стоят соответствующие координаты вектора
. Во втором столбце на аналогичных местах стоят соответствующие координаты вектора  . Последний столбец заполняется при исследовании симплексной таблицы.
. Последний столбец заполняется при исследовании симплексной таблицы.
В первой строке, начиная с 4‑го столбца, располагаются элементы 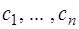 .
.
Во второй строке, начиная с 3‑его столбца – векторы 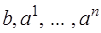 . Под ними – разложения этих векторов по базису
. Под ними – разложения этих векторов по базису  .
.
а) Так как 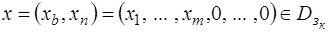 , то
, то 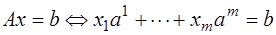 . Это означает, что разложением вектора
. Это означает, что разложением вектора 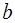 по базису
по базису  является вектор
является вектор 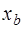 .
.
б) Предположим, что векторы 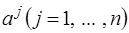 имеют следующее разложение по базису
имеют следующее разложение по базису  :
:
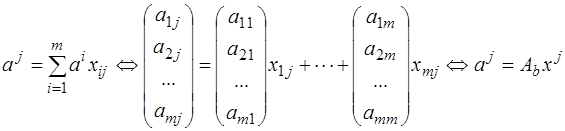 ,
,
где 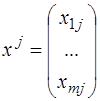 – столбец коэффициентов разложения вектора
– столбец коэффициентов разложения вектора 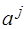 по базису
по базису  . Тогда
. Тогда 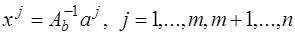 .
.
Для 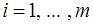 разложения векторов
разложения векторов 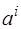 тривиальны:
тривиальны:  , следовательно, вектор‑столбец
, следовательно, вектор‑столбец 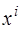 представляет собой единичный вектор. При
представляет собой единичный вектор. При 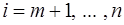 неизвестные вектор-столбцы
неизвестные вектор-столбцы 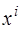 отыскиваются с помощью обратной матрицы.
отыскиваются с помощью обратной матрицы.
в) В предпоследней строке  под вектором
под вектором  выписывается
выписывается 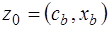 – значение целевой функции в крайней точке. Под векторами
– значение целевой функции в крайней точке. Под векторами 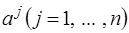 в предпоследнюю строку записываются значения
в предпоследнюю строку записываются значения 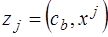 . Очевидно, что при
. Очевидно, что при 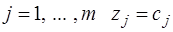 .
.
г) В последнюю строку, начиная с 4‑го столбца, заносится разность между элементами предпоследней строки и элементами первой строки:
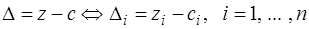 .
.

| 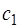
| … | 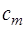
| 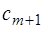
| … | 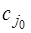
| … | 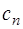
| 
| ||
| базис | 
| 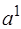
| … | 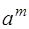
| 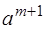
| … | 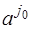
| … | 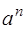
| ||
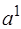
| 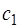
| 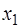
| … | 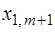
| … | 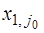
| … | 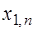
| 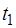
| ||
| … | … | … | … | … | … | … | … | … | … | … | … |
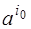
| 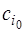
| 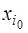
| … | 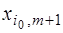
| … | 
| … | 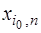
| 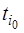
| ||
| … | … | … | … | … | … | … | … | … | … | … | … |
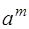
| 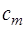
| 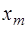
| … | 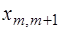
| … | 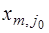
| … | 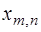
| 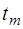
| ||

| 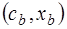
| 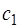
| … | 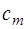
| 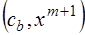
| … | 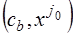
| … | 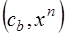
| ||

| … | 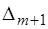
| … | 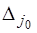
| … | 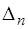
|
4) Исследовать симплексную таблицу.
а) Если 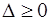 , то крайняя точка
, то крайняя точка 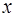 является решением задачи,
является решением задачи, 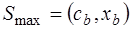 .
.
б) Если для некоторого  имеют место неравенства
имеют место неравенства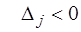 и
и 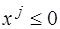 , то
, то  .
.
в) Пусть в строке  имеются отрицательные числа, а соответствующие столбцы содержат положительные числа и
имеются отрицательные числа, а соответствующие столбцы содержат положительные числа и 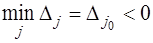 . Тогда столбец индексом
. Тогда столбец индексом 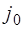 является разрешающим. Введем обозначение:
является разрешающим. Введем обозначение: 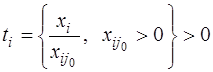 . Эти значения
. Эти значения 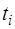 ставим соответственно в последнем столбце таблицы. Пусть
ставим соответственно в последнем столбце таблицы. Пусть 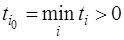 . Тогда строка с номером
. Тогда строка с номером 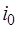 является разрешающей, а разрешающим элементом симплексной таблицы является элемент
является разрешающей, а разрешающим элементом симплексной таблицы является элемент  .
.
Далее необходимо из числа базисных векторов исключить вектор 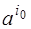 , и вместо него взять вектор
, и вместо него взять вектор 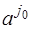 . Значение целевой функции при этом возрастает на величину
. Значение целевой функции при этом возрастает на величину 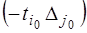 .
.
5) Построить новую симплексную таблицу для базиса 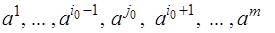 , т.е. векторы
, т.е. векторы 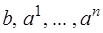 разложить по новому базису.
разложить по новому базису.
Элементы таблицы 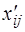 , не лежащие в разрешающем столбце и разрешающей строке, вычисляются по правилу прямоугольника:
, не лежащие в разрешающем столбце и разрешающей строке, вычисляются по правилу прямоугольника:
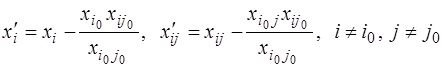 .
.
Элементы разрешающей строки делятся на разрешающий элемент:
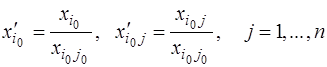 .
.
Далее перейти к исследованию новой симплексной таблице, т.е. к пункту 4).
Симплекс‑метод позволяет решать точно также и вырожденные задачи линейного программирования. Число положительных координат крайней точки в таких задачах меньше 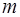 , но число базисных векторов всегда равняется рангу матрицы
, но число базисных векторов всегда равняется рангу матрицы 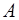 . Перейти от вырожденной задачи к невырожденной можно путем сколь угодно малого изменения начальных данных задачи. В вырожденных задачах возможны холостые шаги симплекс‑метода, т.е. шаги, в результате которых значение целевой функции не изменяется. При этом теоретически возможно и зацикливание, т.е. бесконечное повторение холостых шагов. Для того чтобы избежать зацикливания, разработаны специальные алгоритмы – антициклины (см., например, Ф.П. Васильев «Методы оптимизации». М.: Факториал Пресс, 2002). На практике зацикливание происходит крайне редко, поэтому в данном курсе антициклины не рассматриваются.
. Перейти от вырожденной задачи к невырожденной можно путем сколь угодно малого изменения начальных данных задачи. В вырожденных задачах возможны холостые шаги симплекс‑метода, т.е. шаги, в результате которых значение целевой функции не изменяется. При этом теоретически возможно и зацикливание, т.е. бесконечное повторение холостых шагов. Для того чтобы избежать зацикливания, разработаны специальные алгоритмы – антициклины (см., например, Ф.П. Васильев «Методы оптимизации». М.: Факториал Пресс, 2002). На практике зацикливание происходит крайне редко, поэтому в данном курсе антициклины не рассматриваются.
Пример 1. Решить задачу линейного программирования в канонической форме с заданной начальной крайней точкой 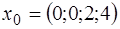 , используя симплекс‑метод:
, используя симплекс‑метод:
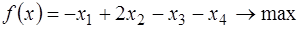 ;
;
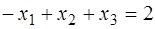 ,
,
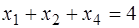 ,
,
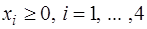 .
.
Решение: Данная задача задана в канонической форме, также задана начальная крайняя точка. Построим симплексную таблицу. Матрица системы ограничений имеет вид:
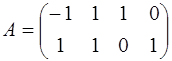 .
.
Базисная матрица задачи состоит из третьего и четвертого столбцов матрицы 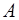 , соответствующих положительным координатам начальной крайней точки:
, соответствующих положительным координатам начальной крайней точки:
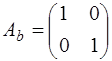 .
.
Так как базисная матрица в данной задаче является единичной, то 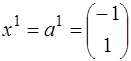 ,
, 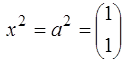 .
.
Построим и заполним симплексную таблицу:

| -1 | -1 | -1 | 
| |||
| базис | 
| 
| 
| 
| 
| ||

| -1 | -1 | |||||
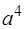
| -1 | ||||||

| -6 | -2 | -1 | -1 | |||
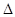
| -4 |
В последней строке таблицы содержится только один отрицательный элемент, соответствующий столбцу  . Поэтому этот столбец будет разрешающим. Заполним соответствующие позиции последнего столбца и выберем минимальный положительный элемент. В данном случае этот минимальный элемент равен 2, он соответствует базисному вектору
. Поэтому этот столбец будет разрешающим. Заполним соответствующие позиции последнего столбца и выберем минимальный положительный элемент. В данном случае этот минимальный элемент равен 2, он соответствует базисному вектору  . Строка, соответствующая
. Строка, соответствующая  , является разрешающей, а вектор
, является разрешающей, а вектор  в базисе следует заменить на
в базисе следует заменить на  . Строим новую симплексную таблицу для нового базиса
. Строим новую симплексную таблицу для нового базиса  ,
,  .
.

| -1 | -1 | -1 | 
| |||
| базис | 
| 
| 
| 
| 
| ||

| -1 | ||||||

| -1 | -1 | |||||

| -4 | -1 | |||||

| -3 |
Из таблицы видно, что разрешающим столбцом является столбец  , содержащий только один положительный элемент, соответствующий
, содержащий только один положительный элемент, соответствующий  . Поэтому разрешающей строкой является строка, соответствующая
. Поэтому разрешающей строкой является строка, соответствующая  . Столбец
. Столбец  в базисе заменяем на столбец
в базисе заменяем на столбец  и для нового базиса строим симплексную таблицу.
и для нового базиса строим симплексную таблицу.

| -1 | -1 | -1 | 
| |||
| базис | 
| 
| 
| 
| 
| ||

| 
| 
| |||||

| -1 | 
| 
| ||||

| -1 | 
| 
| ||||

| 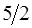
| 
|
Так как 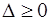 , то точка
, то точка 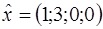 является решением задачи и
является решением задачи и 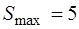 . ●
. ●
Пример 2. Решить задачу линейного программирования в канонической форме с заданной начальной крайней точкой 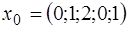 , используя симплекс-метод:
, используя симплекс-метод:
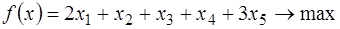 ;
;
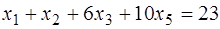 ,
,
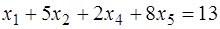 ,
,
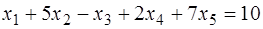 ,
,
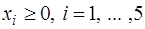 .
.
Матрица системы ограничений и базисная матрица имеют вид:
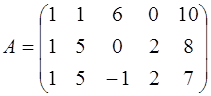 ,
, 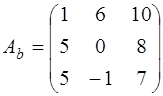 .
.
Найдем матрицу, обратную к 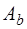 , например, методом присоединенной матрицы. Для этого найдем определитель матрицы
, например, методом присоединенной матрицы. Для этого найдем определитель матрицы 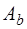 и алгебраические дополнения элементов этой матрицы:
и алгебраические дополнения элементов этой матрицы:
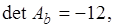
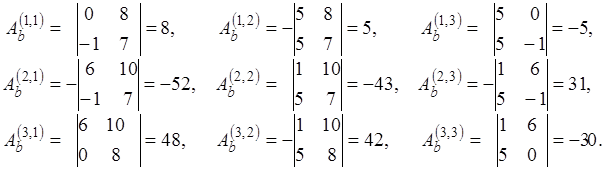
Присоединенная матрица 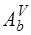 определяется как транспонированная к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы
определяется как транспонированная к матрице, составленной из алгебраических дополнений соответствующих элементов матрицы 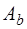 :
:
 .
.
Тогда обратная матрица к 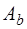 имеет вид:
имеет вид:
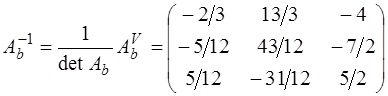 .
.
Далее находим разложения векторов  по базису
по базису 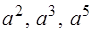 :
:
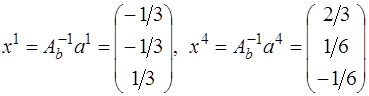 .
.
Разложением вектора 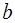 является вектор
является вектор 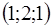 ненулевых координат крайней точки. Составим симплексную таблицу:
ненулевых координат крайней точки. Составим симплексную таблицу:

| 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| ||

| 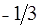
| 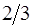
| ||||||

| 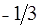
| 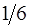
| ||||||

| 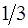
| 
| ||||||

| 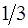
| 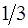
| ||||||

| 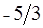
| 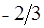
|
В последней строке имеются два отрицательных числа. Меньшее из них соответствует столбцу  . Этот столбец будет разрешающим. В столбце
. Этот столбец будет разрешающим. В столбце  имеется один положительный элемент, соответствующий
имеется один положительный элемент, соответствующий  , поэтому строка
, поэтому строка  будет разрешающей. Из числа базисных векторов исключаем вектор
будет разрешающей. Из числа базисных векторов исключаем вектор  и вместо него вводим вектор
и вместо него вводим вектор  . Строим симплексную таблицу для нового базиса:
. Строим симплексную таблицу для нового базиса:

| 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| ||

| 
| |||||||

| ||||||||

| 
| |||||||

| 
| |||||||

| 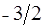
|
Последняя строка новой таблицы содержит один отрицательный элемент, соответствующий вектору  . В соответствующем столбце только одно число является положительным. Это число соответствует вектору
. В соответствующем столбце только одно число является положительным. Это число соответствует вектору  . На следующем этапе из числа базисных векторов исключаем вектор
. На следующем этапе из числа базисных векторов исключаем вектор  и вводим вместо него вектор
и вводим вместо него вектор  . Строим новую симплексную таблицу:
. Строим новую симплексную таблицу:

| 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| ||

| ||||||||

| ||||||||

| ||||||||

| ||||||||

|
Так как 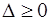 , то точка
, то точка 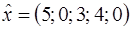 является решением задачи и
является решением задачи и 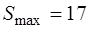 . ●
. ●
– Конец работы –
Эта тема принадлежит разделу:
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств
МЕТОДЫ ОПТИМИЗАЦИИ... ПРАКТИЧЕСКИЕ ЗАНЯТИЯ... Данное учебное пособие создано на основе семестрового курса Методы оптимизации читаемого студентам третьего и...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Программирования.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов