Вариационного исчисления.

 

Рассмотрим некоторое функциональное пространство 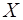. Пусть каждому элементу поставлено в соответствие число 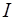. Тогда говорят, что на множестве задан функционал .

Линейное пространство называется нормированным, если на 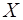определен функционал , называемый нормой и удовлетворяющий условиям:

а) , причем ;

б) ;

в) .

 

Будем рассматривать следующие функциональные пространства:

1) - пространство функций, непрерывных на отрезке 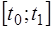с введенной в нем нормой ;

2) 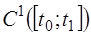- пространство функций, имеющих непрерывную производную на отрезке 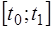с нормой

.

 

Определение. Простейшей задачей классического вариационного исчисления (КВИ) называется следующая экстремальная задача в пространстве :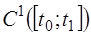

. (з)

Здесь - функция трех переменных, называемая интегрантом, отрезок 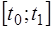фиксирован и конечен, . ▲

Определение. Функции 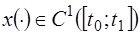, удовлетворяющие краевым условиям 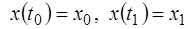, называются допустимыми. ▲

Рис. 8.1

 

Определение. Говорят, что допустимая функция 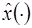доставляет слабый локальный минимум (максимум) в задаче (з), пишут: , если такое, что для любой допустимой функции 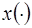, удовлетворяющей условию 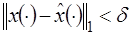, выполнено неравенство

. ▲

 

Теорема. Пусть функция 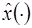доставляет слабый локальный экстремум в поставленной задаче (з) 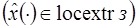, а функции 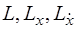непрерывны как функции трех переменных в некоторой окрестности множества . Тогда и функция 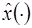удовлетворяет уравнению Эйлера:

. (1)

Здесь использованы следующие обозначения:

.

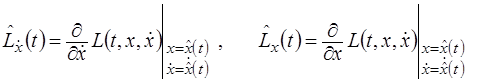Доказательство: Возьмем произвольную, но фиксированную функцию 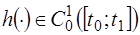, где

.

Рассмотрим функцию одной вещественной переменной

.

Функция является допустимой для любого . Так как , то функция 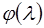имеет экстремум в точке .

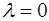Положим . Тогда

.

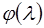Из условий гладкости, наложенных на функции , следует, что функции и дифференцируемы в некотором прямоугольнике , поэтому функция дифференцируема в нуле и по теореме Ферма .

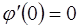Продифференцируем функцию :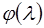

,

. (2)

На следующем этапе доказательства теоремы сформулируем и докажем вспомогательное утверждение.

Лемма Дюбуа-Реймона.

Пусть функции непрерывны на отрезке и

.

Тогда и выполнено равенство

.

Доказательство леммы: Возьмем функцию такую, что

.

Такая функция существует, так как из первого условия функция определяется с точностью до константы, а выбором константы можно удовлетворить второе условие. Тогда для любой функции по условию леммы справедливы равенства:

.

Рассмотрим функцию . Эта функция принадлежит пространству . Действительно,

.

Далее, .

Тогда для функции также должно выполняться равенство . Откуда следует, что . Поэтому и .

Теперь из леммы Дюбуа-Реймона и равенства (2) следует утверждение теоремы. ■

 

Уравнение (1) представляет собой дифференциальное уравнение второго порядка, так что его общее решение должно зависеть от двух произвольных постоянных. Значения этих постоянных определяются из граничных условий

.

Следует отметить, что краевая задача

не всегда имеет решение, а если решение существует, то оно может быть не единственным.

Определение. Функции, удовлетворяющие уравнению Эйлера задачи (з), называются экстремалями, а допустимые функции, удовлетворяющие уравнению Эйлера, называются допустимыми экстремалями. ▲

Интегралы уравнения Эйлера.

1. Если интегрант не зависит явно от 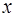, то имеет место интеграл импульса

.

2. Если интегрант не зависит явно от , то имеет место интеграл энергии

.

Для доказательства интеграла энергии умножим обе части равенства (1) на :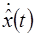

Отметим, что при выводе интеграла энергии использовалось дополнительное предположение о существовании второй производной .

Пример 1. .

Решение: Интегрант задачи равен .

Уравнение Эйлера имеет вид:

.

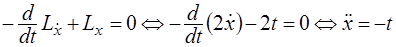Общее решение дифференциального уравнения Эйлера:

.

Постоянные 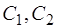найдем из граничных условий:

.

Откуда получаем . Единственная допустимая экстремаль задачи имеет вид:

.

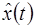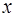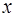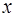Покажем, что доставляет абсолютный минимум в задаче, т.е. покажем, что для любой допустимой функции выполнено неравенство . Представим функцию в виде: . Так как функция должна удовлетворять краевым условиям задачи, то для функции 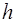краевые условия будут нулевыми: .

Рассмотрим разность :

.

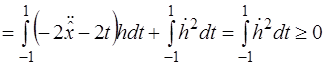Таким образом, для любой допустимой функции разность неотрицательна.

Ответ: .●