рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Программирования.
Реферат Курсовая Конспект
Программирования.
Программирования. - раздел Философия, ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств Постановка Задачи. Общая Постановка Задачи Линейного Про...
Постановка задачи. Общая постановка задачи линейного программирования состоит в нахождении экстремума линейной функции 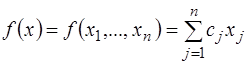 при наличии ограничений, задаваемых в виде линейных уравнений и неравенств:
при наличии ограничений, задаваемых в виде линейных уравнений и неравенств:
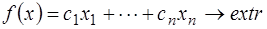
 (1)
(1)
 (2)
(2)
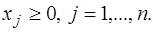 (3)
(3)
Отметим, что в условии задачи линейного программирования могут содержаться неравенства и противоположного, чем в (2) знака, однако, такие неравенства легко сводятся к виду (2) умножением на –1.
Если задача линейного программирования содержит только две переменные, и в ее условии нет ограничений в виде равенств (1), то такую задачу можно решить графически.
Рассмотрим задачу:
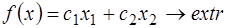 (4)
(4)
 (5)
(5)
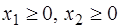 . (6)
. (6)
На плоскости  любое из неравенств (5) определяет полуплоскость, лежащую по одну из сторон прямой
любое из неравенств (5) определяет полуплоскость, лежащую по одну из сторон прямой  . Для того чтобы определить расположение этой полуплоскости относительно граничной прямой, можно подставить координаты какой‑либо точки в соответствующее неравенство (5) и проверить его выполнение. Таким образом, допустимое множество
. Для того чтобы определить расположение этой полуплоскости относительно граничной прямой, можно подставить координаты какой‑либо точки в соответствующее неравенство (5) и проверить его выполнение. Таким образом, допустимое множество 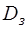 задачи линейного программирования (4)–(6) является пересечением первой четверти, задаваемой неравенствами (6), и полуплоскостей, задаваемых неравенствами (5). Поэтому множество
задачи линейного программирования (4)–(6) является пересечением первой четверти, задаваемой неравенствами (6), и полуплоскостей, задаваемых неравенствами (5). Поэтому множество 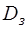 представляет собой одно из множеств на плоскости
представляет собой одно из множеств на плоскости  :
:
а) пустое множество (тогда задача (4)–(6) не имеет решения);
б) выпуклый многоугольник (рис. 5.1);
в) неограниченное многоугольное множество (рис. 5.2);
г) луч;
д) отрезок;
е) точку (тогда эта точка и будет решением задачи).
Для решения задачи линейного программирования в случае, когда  Æ, рассмотрим множество линий уровня функции
Æ, рассмотрим множество линий уровня функции 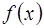 :
:
 . (7)
. (7)
Прямые (7) представляют собой семейство параллельных прямых. Вектор–градиент  перпендикулярен прямым (7) и указывает направление возрастания функции
перпендикулярен прямым (7) и указывает направление возрастания функции 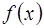 . Если перемешать параллельно самой себе произвольную прямую (7), проходящую через допустимое множество
. Если перемешать параллельно самой себе произвольную прямую (7), проходящую через допустимое множество 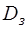 , в направлении
, в направлении 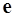 до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с множеством
до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с множеством 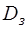 , то в своем крайнем положении указанная прямая пройдет через точку множества
, то в своем крайнем положении указанная прямая пройдет через точку множества 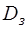 , в которой функция
, в которой функция 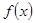 принимает максимальное на
принимает максимальное на 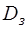 значение. Если перемещать произвольную прямую (6) в противоположном направлении до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с множеством
значение. Если перемещать произвольную прямую (6) в противоположном направлении до тех пор, пока эта прямая будет иметь хотя бы одну общую точку с множеством 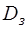 , то получим точку, в которой
, то получим точку, в которой 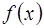 принимает минимальное значение на множестве
принимает минимальное значение на множестве 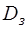 .
.
Заметим, что в случае, когда 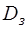 представляет собой неограниченное множество на плоскости
представляет собой неограниченное множество на плоскости  , возможно, что
, возможно, что 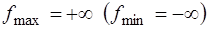 . Если прямая (7) параллельна одной из сторон многоугольника
. Если прямая (7) параллельна одной из сторон многоугольника 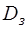 , то решением задачи может быть целый отрезок или даже луч.
, то решением задачи может быть целый отрезок или даже луч.
 |
Рис. 5.1
 |
Рис. 5.2
Пример 1. Решить задачу линейного программирования:
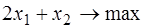

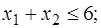
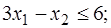
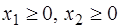 .
.
Решение. Изобразим на плоскости  допустимое множество
допустимое множество 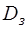 данной задачи. Оно представляет собой многоугольник
данной задачи. Оно представляет собой многоугольник  с вершинами в точках
с вершинами в точках 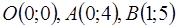 ,
, 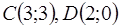 (рис. 5.3). Построим одну из линий уровня целевой функции
(рис. 5.3). Построим одну из линий уровня целевой функции 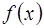
 . Вектор‑градиент
. Вектор‑градиент 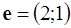 указывает направление возрастания функции
указывает направление возрастания функции 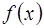 . Совершая параллельный перенос линии уровня вдоль направления
. Совершая параллельный перенос линии уровня вдоль направления 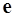 , находим ее крайнее положение. В своем крайнем положении прямая
, находим ее крайнее положение. В своем крайнем положении прямая  проходит через точку
проходит через точку 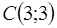 многоугольника
многоугольника 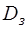 . Откуда следует, что
. Откуда следует, что 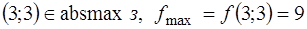 . ●
. ●
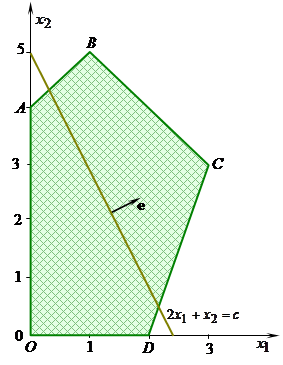 |
Рис. 5.3
Пример 2. Решить задачу линейного программирования:
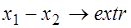

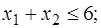
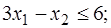
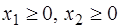 .
.
Решение. Множество допустимых точек этой задачи совпадает с 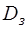 в примере 1 (см. рис. 5.3). Изобразим линию уровня
в примере 1 (см. рис. 5.3). Изобразим линию уровня 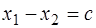 . Вектор
. Вектор 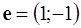 указывает направление возрастания целевой функции (рис. 5.4). Совершая параллельный перенос линии уровня вдоль направления
указывает направление возрастания целевой функции (рис. 5.4). Совершая параллельный перенос линии уровня вдоль направления 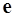 , получим, что максимальное значение целевая функция достигает в точке
, получим, что максимальное значение целевая функция достигает в точке 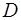 . Поэтому
. Поэтому 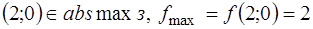 .
.
Перемещая линию уровня параллельно самой себе в противоположном направлении, получим, что в своем крайнем положении она содержит отрезок  . Любая точка отрезка
. Любая точка отрезка  представима в виде:
представима в виде: 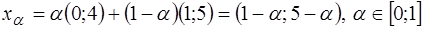 . Поэтому
. Поэтому 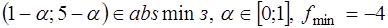 . ●
. ●
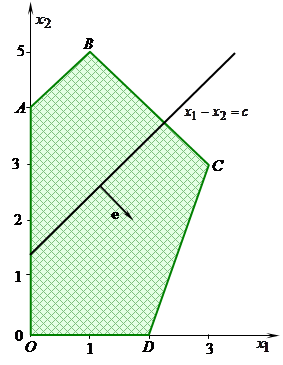 |
Рис 5.4
Пример 3. Решить задачу линейного программирования:

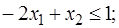
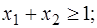
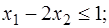
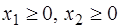 .
.
Решение. Допустимое множество 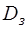 данной задачи представляет собой неограниченное многоугольное множество (рис. 5.5). Функция
данной задачи представляет собой неограниченное многоугольное множество (рис. 5.5). Функция 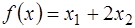 возрастает в направлении
возрастает в направлении 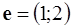 . При параллельном переносе прямой
. При параллельном переносе прямой 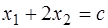 в направлении
в направлении 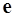 функция
функция 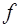 неограниченно возрастает. Поэтому
неограниченно возрастает. Поэтому 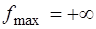 . При параллельном переносе прямой
. При параллельном переносе прямой 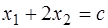 в противоположном направлении крайней точкой пересечения этой прямой с
в противоположном направлении крайней точкой пересечения этой прямой с 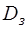 является точка
является точка 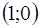 . Следовательно,
. Следовательно, 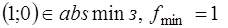 . ●
. ●
Графический метод используется также для задач линейного программирования в общей постановке, если отсутствует ограничение (2), а число свободных переменных системы (1) не больше двух.
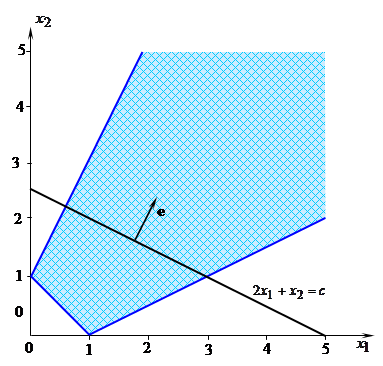 |
Рис. 5.5
Пример 4. Решить задачу линейного программирования:

 ;
;
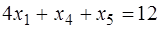 ;
;
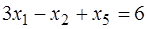 ;
;
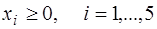 .
.
Решение. Матрица системы ограничений имеет вид:
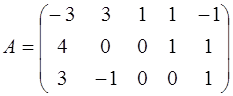 .
.
Ранг этой матрицы равен 3. Число свободных переменных равно 5-3=2. Выберем в качестве базисного минора мир, образованный последними тремя столбцами матрицы 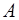 и разрешим систему ограничений-равенств относительно базисных переменных
и разрешим систему ограничений-равенств относительно базисных переменных  . Т.е. выразим базисные переменные
. Т.е. выразим базисные переменные 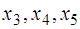 через свободные
через свободные 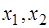 . Получим:
. Получим:
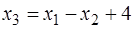 ,
,
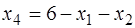 ;
;
 .
.
Подставим эти значения 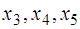 в целевую функцию, тогда целевая функция примет вид:
в целевую функцию, тогда целевая функция примет вид:
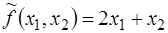 .
.
С учетом условия 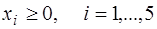 , получим следующую задачу:
, получим следующую задачу:
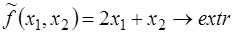

 ,
,
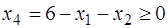 ;
;
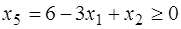 .
.
Полученная задача совпадает с задачей в примере 1. Поэтому 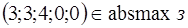 ,
, . ●
. ●
Во многих случаях на допустимое множество задачи линейного программирования (1)–(3) накладывается дополнительное требование целочисленности переменных  . Если этому требованию должны удовлетворять все переменные, то получаем полностью целочисленную задачу линейного программирования. Полностью целочисленную задачу линейного программирования с двумя переменными (4)-(6) можно решить графически, учитывая, что допустимое множество
. Если этому требованию должны удовлетворять все переменные, то получаем полностью целочисленную задачу линейного программирования. Полностью целочисленную задачу линейного программирования с двумя переменными (4)-(6) можно решить графически, учитывая, что допустимое множество 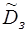 этой задачи состоит из точек целочисленной координатной сетки, принадлежащих множеству
этой задачи состоит из точек целочисленной координатной сетки, принадлежащих множеству 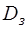 задачи линейного программирования без дополнительного требования
задачи линейного программирования без дополнительного требования
 |
Рис. 5.6
Пример 5. Найти решение целочисленной задачи линейного программирования:
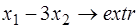
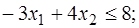
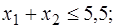
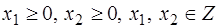 .
.
Решение. На плоскости  построим допустимое множество рассматриваемой задачи без требования целочисленности переменных
построим допустимое множество рассматриваемой задачи без требования целочисленности переменных  . Получим многоугольник
. Получим многоугольник 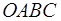 (рис. 5.6). Отметим внутри этого многоугольника точки с целочисленными координатами. Совокупность этих точек представляет собой допустимое множество
(рис. 5.6). Отметим внутри этого многоугольника точки с целочисленными координатами. Совокупность этих точек представляет собой допустимое множество 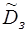 полностью целочисленной задачи. Перемещая линию уровня
полностью целочисленной задачи. Перемещая линию уровня 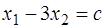 в направлении
в направлении 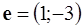 возрастания функции
возрастания функции 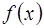 , находим крайнее положение этой линии, в котором она еще имеет непустое пересечение с множеством
, находим крайнее положение этой линии, в котором она еще имеет непустое пересечение с множеством 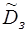 . Получаем точку
. Получаем точку 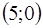 . Следовательно
. Следовательно 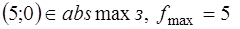 . Перемещая линию уровня в направлении, противоположном вектору
. Перемещая линию уровня в направлении, противоположном вектору 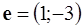 , получим решение задачи на минимум:
, получим решение задачи на минимум: 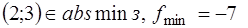 . ●
. ●
– Конец работы –
Эта тема принадлежит разделу:
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств
МЕТОДЫ ОПТИМИЗАЦИИ... ПРАКТИЧЕСКИЕ ЗАНЯТИЯ... Данное учебное пособие создано на основе семестрового курса Методы оптимизации читаемого студентам третьего и...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Программирования.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов