рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Метод потенциалов.
Реферат Курсовая Конспект
Метод потенциалов.
Метод потенциалов. - раздел Философия, ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств 1) Привести Задачу К Замкнутой Модели. 2) Найти Первоначальный План ...
1) Привести задачу к замкнутой модели.
2) Найти первоначальный план перевозок 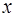 (начальную крайнюю точку множества допустимых элементов).
(начальную крайнюю точку множества допустимых элементов).
3) Провести исследование плана перевозок 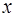 . Для найденного плана перевозок построить матрицу
. Для найденного плана перевозок построить матрицу  . Переменные
. Переменные  называются потенциалами. Они определяются из системы
называются потенциалами. Они определяются из системы  уравнений
уравнений  для базисных индексов
для базисных индексов  . Для однозначного определения потенциалов положим один из потенциалов равным заданной величине, например,
. Для однозначного определения потенциалов положим один из потенциалов равным заданной величине, например,  .
.
4) Провести исследование матрицы
 .
.
Если 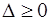 , то исследуемый план перевозок
, то исследуемый план перевозок 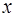 является решением задачи. Если среди элементов матрицы
является решением задачи. Если среди элементов матрицы  есть отрицательные, то выберем наименьший элемент. Пусть, например,
есть отрицательные, то выберем наименьший элемент. Пусть, например,  .
.
5) Построить новый план перевозок, являющийся крайней точкой множества допустимых элементов:  , где
, где

Здесь  выбирается так, чтобы одна из базисных компонент обратилась в ноль, а остальные были по-прежнему неотрицательны. Тогда вектор матрицы
выбирается так, чтобы одна из базисных компонент обратилась в ноль, а остальные были по-прежнему неотрицательны. Тогда вектор матрицы 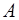 , соответствующий этой компоненте, выводим из числа базисных, а вектор матрицы
, соответствующий этой компоненте, выводим из числа базисных, а вектор матрицы 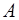 , соответствующий переменной
, соответствующий переменной  , вводим в число базисных векторов. Здесь под матрицей
, вводим в число базисных векторов. Здесь под матрицей 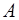 понимается матрица ограничений задачи, задаваемых уравнениями (1), (2).
понимается матрица ограничений задачи, задаваемых уравнениями (1), (2).
Далее вновь начинаем исследование полученной крайней точки  , т.е. возвращаемся к пункту 3).
, т.е. возвращаемся к пункту 3).
В невырожденной задаче в ноль может обратиться только одна из компонент вектора 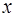 . В вырожденной задаче в ноль может обратиться несколько компонент. В этом случае из числа базисных векторов исключается любой вектор с нулевым значением, как правило, исключается вектор с наибольшей стоимостью перевозок.
. В вырожденной задаче в ноль может обратиться несколько компонент. В этом случае из числа базисных векторов исключается любой вектор с нулевым значением, как правило, исключается вектор с наибольшей стоимостью перевозок.
Пример 2. Решить транспортную задачу, заданную платежной матрицей (табл. 7.1).
Решение:
1) В примере 1 задача была приведена к замкнутой модели. Соответствующая платежная матрица представлена таблицей 7.2.
2) в качестве первоначального плана перевозок возьмем план, полученный методом «минимум по матрице» и представленный таблицей 7.4.
3) Построим матрицу  :
:

| 
| 
| |

| |||

| |||
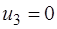
|
4) Найдем матрицу  :
:
 .
.
В качестве наименьшего отрицательного элемента матрицы  возьмем
возьмем  .
.
5) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента  величину
величину  :
:

| 
| |

| 
|

Перейдем к пункту  ).
).
 ) Построим матрицу
) Построим матрицу  :
:

| 
| 
| |

| |||

| |||

|
 ) Найдем матрицу
) Найдем матрицу  :
:
 .
.
Наименьший отрицательный элемент полученной матрицы  :
:  . Добавляя в предыдущий план перевозок на место нулевого небазисного элемента
. Добавляя в предыдущий план перевозок на место нулевого небазисного элемента  величину
величину  , получим третий план перевозок. Вычислим значение функционала
, получим третий план перевозок. Вычислим значение функционала  для второго плана перевозок:
для второго плана перевозок:
 .
.
 ) Построим новый план перевозок:
) Построим новый план перевозок:

| 
| |

| 
|

 ) Построим матрицу
) Построим матрицу  :
:

| 
| 
| |

| |||

| |||

| -2 |
 ) Найдем матрицу
) Найдем матрицу  :
:
 .
.
Так как 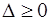 , то третий план перевозок, полученный в пункте
, то третий план перевозок, полученный в пункте  ), является оптимальным. Найдем значение функционала
), является оптимальным. Найдем значение функционала  :
:
 .
.
Заметим, что в исходной задаче, задаваемой платежной матрицей в виде таблицы 7.1, пункт отправления  отсутствовал, он был искусственно введен для сведения задачи к замкнутой модели. Тот факт, что в полученном плане перевозок
отсутствовал, он был искусственно введен для сведения задачи к замкнутой модели. Тот факт, что в полученном плане перевозок  ,
,  , означает, что пункты назначения
, означает, что пункты назначения  не будут полностью обслужены. Выпишем ответ для поставленной задачи.
не будут полностью обслужены. Выпишем ответ для поставленной задачи.
Ответ:  . ●
. ●
Пример 3. Решить транспортную задачу, заданную платежной матрицей (табл. 7.5).
Таблица 7.5

| 
| 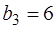
| 
| |

| ||||

| ||||

| ||||
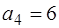
|
Решение:
1) В данной задаче  , т.е. имеем замкнутую модель транспортной задачи.
, т.е. имеем замкнутую модель транспортной задачи.
2) Методом северно-западного угла найдем начальный план перевозок:

| 
| 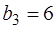
| 
| |

| ||||

| ||||

| ||||
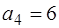
|
3) Построим матрицу  :
:

| 
| 
| 
| |

| ||||

| ||||

| ||||

|
4) Найдем матрицу  :
:
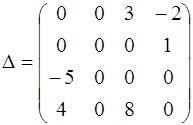 .
.
Наименьший отрицательный элемент матрицы  равен
равен  .
.
5) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента  величину
величину  :
:

| 
| ||

| 
| ||

Заметим, что здесь обратились в ноль два элемента  и
и  . Исключим из числа базисных компонент элемент
. Исключим из числа базисных компонент элемент  с большей стоимостью перевозки.
с большей стоимостью перевозки.
Перейдем к пункту  ).
).
 ) Построим матрицу
) Построим матрицу  :
:

| 
| 
| 
| |

| ||||

| ||||

| ||||

| -4 | -3 | -5 |
 ) Найдем матрицу
) Найдем матрицу  :
:

Наименьший отрицательный элемент матрицы  равен
равен  .
.
 ) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента
) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента  величину
величину  :
:
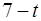
| 
| ||

| 
| ||

 ) Построим матрицу
) Построим матрицу  :
:

| 
| 
| 
| |

| ||||

| ||||

| ||||
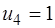
|
 ) Найдем матрицу
) Найдем матрицу  :
:

Наименьший отрицательный элемент матрицы  равен
равен  .
.
 ) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента
) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента  величину
величину  :
:

| |||

| 
| ||

|

 ) Построим матрицу
) Построим матрицу  :
:

| 
| 
| 
| |

| ||||

| ||||

| ||||
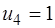
|
 ) Найдем матрицу
) Найдем матрицу  :
:
 .
.
Так как 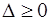 , то четвертый план перевозок, полученный в пункте
, то четвертый план перевозок, полученный в пункте  ), является оптимальным. Найдем значение функционала
), является оптимальным. Найдем значение функционала  :
:
 .
.
Ответ:  . ●
. ●
Пример 4. Решить транспортную задачу, заданную платежной матрицей (табл. 7.6), при дополнительном требовании полного вывоза груза из пункта 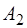 .
.
Таблица 7.6

| 
| |

| ||

|
Решение:
1) Так как 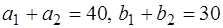 , то
, то  . Для приведения к замкнутой модели введем фиктивный пункт назначения
. Для приведения к замкнутой модели введем фиктивный пункт назначения 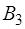 с требуемой величиной ввоза
с требуемой величиной ввоза  . Так как в задаче имеется дополнительное требование полного удовлетворения вывоза груза из пункта
. Так как в задаче имеется дополнительное требование полного удовлетворения вывоза груза из пункта 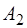 , то положим
, то положим  , где
, где 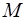 - достаточно большое положительное число. Получим замкнутую модель транспортной задачи со следующей платежной матрицей:
- достаточно большое положительное число. Получим замкнутую модель транспортной задачи со следующей платежной матрицей:

| 
| 
| |

| |||

| 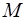
|
2) Найдем начальный план перевозок методом «северо-западного угла».
Первоначальный план перевозок:

| 
| 
| |

| |||

|
3) Построим матрицу  :
:

| 
| 
| |

| 
| ||

| 
|
4) Найдем матрицу  :
:
 .
.
Так как 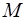 - достаточно большое число, то
- достаточно большое число, то  .
.
5) Построим новый план перевозок, добавляя в предыдущий план перевозок на место нулевого небазисного элемента  величину
величину  :
:
|

| t | |

| 
|
 ) Построим матрицу
) Построим матрицу  :
:

| 
| 
| |

| |||

|
 ) Найдем матрицу
) Найдем матрицу  :
:
 .
.
Так как 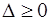 , то полученный в пункте 5) план перевозок является оптимальным. При этом из пункта
, то полученный в пункте 5) план перевозок является оптимальным. При этом из пункта 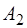 весь груз будет вывезен, а в пункте
весь груз будет вывезен, а в пункте 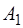 останется 10 единиц груза. Найдем значение функционала
останется 10 единиц груза. Найдем значение функционала  :
:
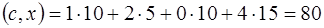 .
.
Ответ:  . ●
. ●
– Конец работы –
Эта тема принадлежит разделу:
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств
МЕТОДЫ ОПТИМИЗАЦИИ... ПРАКТИЧЕСКИЕ ЗАНЯТИЯ... Данное учебное пособие создано на основе семестрового курса Методы оптимизации читаемого студентам третьего и...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод потенциалов.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?








Новости и инфо для студентов