рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Начальной крайней точки
Реферат Курсовая Конспект
Начальной крайней точки
Начальной крайней точки - раздел Философия, ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств Рассмотрим Задачу Линейного Программирования В Канонической Ф...
Рассмотрим задачу линейного программирования в канонической форме:
 , (зк)
, (зк)
где 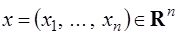 – неизвестная переменная,
– неизвестная переменная,  и
и  – заданные векторы,
– заданные векторы, 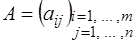 – заданная матрица размера
– заданная матрица размера  . Будем считать, что
. Будем считать, что  (если
(если 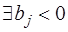 , то умножим обе части
, то умножим обе части  -го уравнения на (-1)).
-го уравнения на (-1)).
Рассмотрим вспомогательную задачу, добавляя искусственные переменные 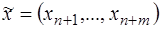 и единичную матрицу
и единичную матрицу 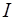 :
:
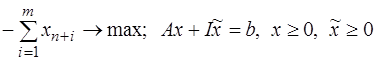 .
. 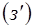
Точка 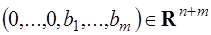 является начальной крайней точкой для вспомогательной задачи
является начальной крайней точкой для вспомогательной задачи 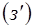 . Решение задачи
. Решение задачи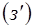 имеет вид:
имеет вид:  . Тогда точка
. Тогда точка  является начальной крайней точкой исходной задачи (зк).
является начальной крайней точкой исходной задачи (зк).
Пример 3. Решить задачу линейного программирования симплекс-методом, находя начальную крайнюю точку методом искусственного базиса.
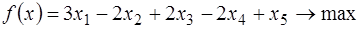 ;
;
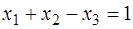 ,
,
 ,
,
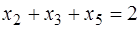
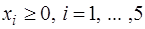 .
.
Решение: Составим вспомогательную задачу:
 ;
;
 ,
,
 ,
,

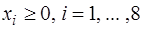 .
.
Начальной крайней точкой вспомогательной задачи является точка 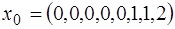 . Заметим, что базисная матрица вспомогательной задачи есть единичная матрица. Поэтому
. Заметим, что базисная матрица вспомогательной задачи есть единичная матрица. Поэтому 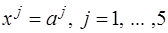 . Построим симплексную таблицу:
. Построим симплексную таблицу:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| -1 | -1 | |||||||||

| -1 | -1 | |||||||||

| -1 | ||||||||||

| -4 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||

| -1 | -1 | -1 | -1 | -1 |
В последней строке содержится 5 одинаковых отрицательных чисел. Для определенности в качестве разрешающего столбца возьмем столбец  . Так как в соответствующем столбце содержится только один положительный элемент, то соответствующая строка
. Так как в соответствующем столбце содержится только один положительный элемент, то соответствующая строка  будет разрешающей. Исключаем из базиса вектор
будет разрешающей. Исключаем из базиса вектор  и заменяем его на
и заменяем его на 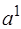 . Строим новую симплексную таблицу:
. Строим новую симплексную таблицу:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| -1 | ||||||||||

| -1 | -1 | |||||||||

| -1 | ||||||||||

| -3 | -2 | -1 | -1 | -1 | -1 | |||||

| -2 | -1 | -1 |
Минимальным отрицательным элементом в последней строке является элемент -2, соответствующий вектору  . Столбец
. Столбец  будет разрешающим. В этом столбце имеется два положительных элемента, поэтому заполняем последний столбец таблицы и находим наименьшее из получившихся чисел. Соответствующая строка
будет разрешающим. В этом столбце имеется два положительных элемента, поэтому заполняем последний столбец таблицы и находим наименьшее из получившихся чисел. Соответствующая строка  является разрешающей.
является разрешающей.
Выводим из базиса вектор  и строим таблицу для нового базиса
и строим таблицу для нового базиса  :
:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| |||||||||||

| -1 | ||||||||||

| -1 | -1 | -1 | ||||||||

| -1 | -2 | -1 | -1 | |||||||

| -2 | -1 |
Минимальным отрицательным элементом в последней строке является элемент -2, соответствующий вектору  . Столбец
. Столбец  будет разрешающим. В этом столбце имеется одно положительное число, поэтому строка
будет разрешающим. В этом столбце имеется одно положительное число, поэтому строка  является разрешающей. Строим таблицу для базиса
является разрешающей. Строим таблицу для базиса 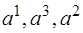 :
:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| |||||||||||

| 
| 
| 
| 
| 
| ||||||

| 
| 
| 
| 
| 
| ||||||

| |||||||||||

|
Так как 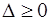 , то точка
, то точка 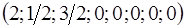 является решением вспомогательной задачи, а точка
является решением вспомогательной задачи, а точка  является начальной крайней точкой исходной задачи. Используя полученные разложения векторов по базису
является начальной крайней точкой исходной задачи. Используя полученные разложения векторов по базису 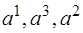 , строим симплексную таблицу исходной задачи:
, строим симплексную таблицу исходной задачи:

| -2 | -2 | 
| |||||
| базис | 
| 
| 
| 
| 
| 
| ||

| ||||||||

| 
| 
| 
| |||||

| -2 | 
| 
| 
| ||||

| -2 | |||||||

| -1 |
Последняя строка содержит один отрицательный элемент, соответствующий вектору  . Вычисляем элементы последнего столбца и выбираем наименьший положительный, соответствующий разрешающей строке
. Вычисляем элементы последнего столбца и выбираем наименьший положительный, соответствующий разрешающей строке  . Для нового базиса
. Для нового базиса 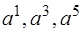 строим таблицу:
строим таблицу:

| -2 | -2 | 
| |||||
| базис | 
| 
| 
| 
| 
| 
| ||

| ||||||||

| -1 | |||||||

| -1 | |||||||

| ||||||||

|
Так как 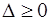 , то
, то  является решением задачи,
является решением задачи, 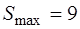 .
.
Замечание. В данной задаче можно было ограничиться введением одной искусственной переменной  , так как два последних столбца матрицы
, так как два последних столбца матрицы 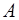 задачи являются столбцами единичной матрицы. Тогда число шагов значительно бы уменьшилось. ●
задачи являются столбцами единичной матрицы. Тогда число шагов значительно бы уменьшилось. ●
Пример 4. Решить задачу линейного программирования:
 ; (з)
; (з)
 ,
,
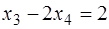 ,
,
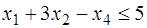 ,
,
 .
.
На первом шаге приведем данную задачу к канонической форме, введя дополнительные переменные  . Получим следующую задачу:
. Получим следующую задачу:
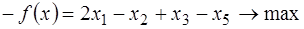 ; (з1)
; (з1)
 ,
,
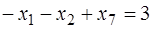 ,
,
 ,
,
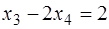 ,
,  .
.
Полученную задачу линейного программирования (з1) в канонической форме будем решать методом искусственного базиса. Для этого рассмотрим вспомогательную задачу, добавляя искусственные переменные 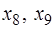 :
:
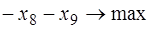 ; (з2)
; (з2)
 ,
,
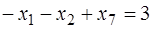 ,
,
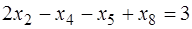 ,
,
 ,
,  .
.
Начальная крайняя точка задачи (з2)  . Базисные векторы
. Базисные векторы
 .
.
Составим симплексную таблицу для задачи (з2):

| -1 | -1 | 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| -1 | 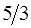
| ||||||||||

| -1 | -1 | ||||||||||

| -1 | -1 | -1 | 
| ||||||||

| -1 | -2 | ||||||||||

| -5 | -2 | -1 | -1 | -1 | |||||||

| -2 | -1 |
Из таблицы видно, что разрешающим столбцом является столбец  , а разрешающей строкой
, а разрешающей строкой  . Заменяем в базисе вектор
. Заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| -1 | -1 | 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 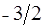
| ||||||||

| 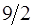
| -1 | 
| 
| 
| |||||||

| 
| 
| 
| 
| ||||||||

| -1 | -2 | ||||||||||

| -2 | -1 | -1 | |||||||||

| -1 |
Заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| -1 | -1 | 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 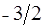
| ||||||||

| 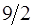
| -1 | 
| 
| 
| |||||||

| 
| 
| 
| 
| ||||||||

| -2 | |||||||||||

| ||||||||||||

|
Вектор 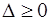 , поэтому точка
, поэтому точка 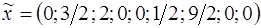 является решением вспомогательной задачи (з2). Тогда точка
является решением вспомогательной задачи (з2). Тогда точка  является начальной крайней точкой задачи линейного программирования в канонической форме (з1).
является начальной крайней точкой задачи линейного программирования в канонической форме (з1).
Приступим к решению задачи (з1). Составим первую симплексную таблицу для начальной крайней точки  . Разложения векторов
. Разложения векторов 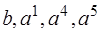 возьмем из последней симплексной таблицы:
возьмем из последней симплексной таблицы:

| 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| |||||||

| 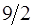
| -1 | 
| 
| ||||||

| -1 | 
| 
| 
| ||||||

| -2 | |||||||||

| 
| -1 | 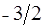
| 
| ||||||

| -2 | 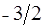
| 
|
Из таблицы видно, что разрешающим столбцом является столбец  , а разрешающей строкой
, а разрешающей строкой  . Заменяем в базисе вектор
. Заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| |||||||

| ||||||||||

| -1 | 
| 
| 
| ||||||

| -2 | |||||||||

| 
| -1 | 
| 
| ||||||

| 
| 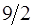
|
Далее заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| ||

| ||||||||||

| ||||||||||

| -1 | |||||||||

| 
| |||||||||

| -1 | 
| ||||||||

| 
|
Так как 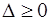 , то точка
, то точка 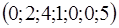 является решением задачи (з1). Тогда точка
является решением задачи (з1). Тогда точка 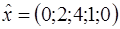 является решением исходной задачи (з).
является решением исходной задачи (з).
Ответ: 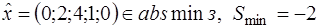 . ●
. ●
– Конец работы –
Эта тема принадлежит разделу:
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ Гладкие конечномерные экстремальные задачи с ограничениями типа равенств
МЕТОДЫ ОПТИМИЗАЦИИ... ПРАКТИЧЕСКИЕ ЗАНЯТИЯ... Данное учебное пособие создано на основе семестрового курса Методы оптимизации читаемого студентам третьего и...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Начальной крайней точки
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов