Теорема Ляпунова

В природе, как известно, широко распространён нормальный закон распределения. Практикой установлено, что этому закону подчиняются ошибки стрельбы и бомбометания, погрешности измерений, погрешности размеров деталей, изготавливаемых промышленными предприятиями, время безотказной работы многих устройств и т.д. Поэтому в процессе обработки экспериментальной информации часто выдвигается предположение о нормальном распределении исследуемой случайной величины. Однако иногда нормальный закон распределения применить нельзя. Ввиду этого необходимо точно знать, когда можно выдвинуть такое предположение и в каких случаях от него следует отказаться. Этому вопросу посвящена центральная предельная теорема и её разновидности (теоремы Ляпунова, Муавра-Лапласа).

Теорема. Если последовательность независимых случайных величин 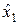, ,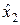…, 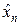удовлетворяет условию Ляпунова

,

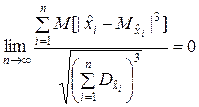где 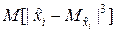– третий абсолютный центральный момент, то последовательность случайных величин

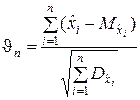
сходится по распределению к случайной величине, имеющей нормальное распределение, т.е. существует предел

.

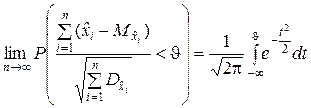На практике часто пользуются случайными величинами, представляющими собой сумму независимых случайных величин:

.

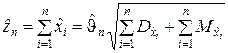Поскольку случайная величина 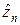связана со случайной величиной 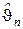линейной зависимостью, то в пределе она также будет иметь нормальное распределение. Параметры данного распределения можно выразить с помощью теорем о числовых характеристиках:

Условие Ляпунова представляет собой требование малости слагаемых

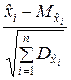
в сумме

.

Таким образом, сущность центральной предельной теоремы состоит в следующем: закон распределения суммы независимых случайных величин при неограниченном увеличении числа слагаемых приближается к нормальному, если случайные величины, входящие в сумму, имеют дисперсию одного и того же порядка и конечные математические ожидания. Это означает, что удельный вес каждого слагаемого стремится к нулю при увеличении числа слагаемых.

В реальных условиях любое случайное отклонение от закономерного протекания основного явления вызывается бесчисленным множеством случайных факторов, каждый из которых обычно оказывает малое влияние на суммарное воздействие, и часто эти факторы независимы или слабо зависимы. Этим и объясняется широкое распространение нормального закона.

На практике теоремой Ляпунова пользуются и тогда, когда n сравнительно невелико. При суммировании непрерывных случайных величин, имеющих одинаковые симметричные законы распределения с одинаковыми числовыми характеристиками, эту теорему можно применять при n ³ 8. Если же суммируются случайные величины с различными несимметричными законами и различными числовыми характеристиками, то теоремой Ляпунова можно пользоваться только при числе слагаемых порядка сотни.

Практическое применение теоремы Ляпунова предполагает использование формул для определения вероятности попадания нормально распределённой случайной величины в интервал [a; b). В данном случае можно воспользоваться следующими формулами:

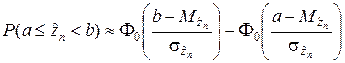; (2.2.1)

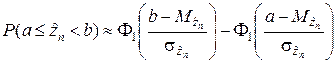, (2.2.2)

где

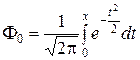, (2.2.3)

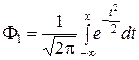(2.2.4)

называются функциями нормированного нормального распределения (т. е. распределения с параметрами 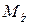= 0, ) или функциями Лапласа, они являются табличными (см. приложения 2 и 3).

Следует отметить, что формулами (2.2.1) и (2.2.2) можно пользоваться при выполнении условия

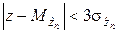, (2.2.5)

где z принимает значение a или b. Это требование вызвано тем, что за пределами интервала

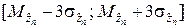
могут быть существенные ошибки.

П р и м е р 2.1. При обработке информации требуется сложить 1000 чисел, каждое из которых округлено с точностью до 0,01. Полагая, что ошибки округления подчинены равномерному закону распределения, найти вероятность того, что суммарная ошибка округления не превысит 0,2.

▼ Обозначим через 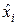, 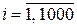ошибку округления i-го числа, а через 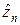– суммарную ошибку округления (n = 1000).

Далее учитываем, что случайная величина, равномерно распределённая на интервале [a; b] имеет математическое ожидание и дисперсию, которые определяются по формулам

, .

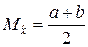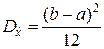Ошибки округления в данном случае распределены на интервале

[a; b] = [–0,005; 0,005],

следовательно,

, .

; ;

.

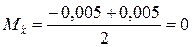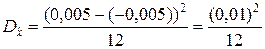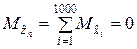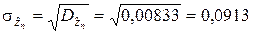Условие (2.2.5) соблюдается, поэтому

Последнее равенство вытекает непосредственно из формулы (2.2.1), в нём учтено, что функция Ф₀(x) является нечётной.

▲