рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Теорема Муавра-Лапласа
Реферат Курсовая Конспект
Теорема Муавра-Лапласа
Теорема Муавра-Лапласа - раздел Образование, Теоретические основы параметрических методов обработки экспериментальных данных Пусть Производится N Независимых Испытаний, В Каждом Из Которых Событи...
Пусть производится n независимых испытаний, в каждом из которых событие A может появляться с одной и той же вероятностью. Тогда случайная величина 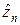 , представляющая собой число появлений события A в n испытаниях, будет иметь биномиальное распределение [4]. Если число испытаний велико, то и случайная величина принимает большое число возможных значений. Пользоваться такой случайной величиной затруднительно из-за сложности вычислений. Поэтому целесообразно применять теорему Муавра-Лапласа, которая доказывает сходимость последовательности случайных величин, имеющих биномиальное распределение, к нормально распределённой случайной величине.
, представляющая собой число появлений события A в n испытаниях, будет иметь биномиальное распределение [4]. Если число испытаний велико, то и случайная величина принимает большое число возможных значений. Пользоваться такой случайной величиной затруднительно из-за сложности вычислений. Поэтому целесообразно применять теорему Муавра-Лапласа, которая доказывает сходимость последовательности случайных величин, имеющих биномиальное распределение, к нормально распределённой случайной величине.
Теорема. Пусть 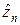 число появлений события A в n независимых испытаниях, в каждом из которых вероятность этого события равна p. Тогда при n ® ¥ имеет место соотношение
число появлений события A в n независимых испытаниях, в каждом из которых вероятность этого события равна p. Тогда при n ® ¥ имеет место соотношение

где q = 1– p; 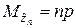 ,
, 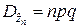 – соответственно математическое ожидание и дисперсия биномиально распределённой случайной величины.
– соответственно математическое ожидание и дисперсия биномиально распределённой случайной величины.
Таким образом, нормированная случайная величина
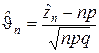 (2.2.6)
(2.2.6)
согласно теореме Муавра-Лапласа в пределе будет подчиняться нормированному нормальному закону распределения. Отсюда вытекает приближённое равенство, справедливое при больших значениях n:
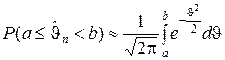 . (2.2.7)
. (2.2.7)
Найдём вероятность попадания случайной величины 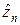 в интервал [m1; m2). Для этого подставим граничные точки m1 и m2 в формулу (2.2.6):
в интервал [m1; m2). Для этого подставим граничные точки m1 и m2 в формулу (2.2.6):
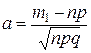 ;
;  .
.
Выражение (2.2.7) принимает вид
 .
.
Используя табличные функции (2.2.3) и (2.2.4), получаем следующие рабочие формулы:
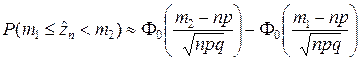 ; (2.2.8)
; (2.2.8)  ; (2.2.9)
; (2.2.9)
Если n сравнительно мало и разность |m – np| соизмерима с 0,5, то не безразлично, относятся ли граничные точки интервала [m1; m2) к числу возможных значений 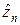 или нет. В этом случае вместо z1 и z2 следует брать m1 – 0,5, m2 – 0,5. Тогда соотношения (2.2.8) и (2.2.9) примут вид
или нет. В этом случае вместо z1 и z2 следует брать m1 – 0,5, m2 – 0,5. Тогда соотношения (2.2.8) и (2.2.9) примут вид
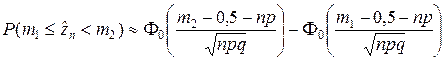 ; (2.2.10)
; (2.2.10) 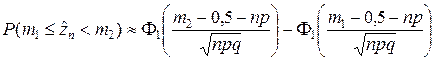 . (2.2.11)
. (2.2.11)
Следует отметить, что формулы (2.2.10) и (2.2.11) дают более точное приближение, чем (2.2.8) и (2.2.9).
Расчёты по приближённым формулам (2.2.8) – (2.2.11) могут производиться при соблюдении условия
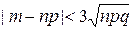 ,
,
которое непосредственно вытекает из (2.2.5).
Теорема Муавра-Лапласа описывает поведение биномиального распределения при больших значениях n, что позволяет значительно упростить вычисления. Расчёты по точной формуле
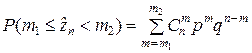 (2.2.12)
(2.2.12)
при больших значениях n очень громоздки.
В выражение (2.2.12) входит число сочетаний из n элементов по m:
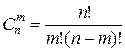 ,
,
где n! = 1×2×…×n, m! = 1×2×…×m.
П р и м е р 2.2. По линии связи независимо друг от друга передаётся 90 сообщений, каждое из которых состоит из пяти двоичных чисел. Вероятность искажения хотя бы одного числа в сообщении равна 0,06. Определить вероятность того, что число принятых без искажения сообщений будет находиться в интервале [82; 87].
▼ Обозначим через 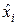 число неискажённых сообщений при i-й передаче. Эта случайная величина принимает значение ноль с вероятностью 0,06 и единица – с вероятностью 0,94. Следовательно
число неискажённых сообщений при i-й передаче. Эта случайная величина принимает значение ноль с вероятностью 0,06 и единица – с вероятностью 0,94. Следовательно
pi = p = 0,94; qi = q = 0,06.
Обозначим 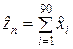 – общее число неискажённых сообщений. Тогда
– общее число неискажённых сообщений. Тогда
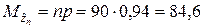 ,
,
 .
.
По формуле (2.2.9) получаем
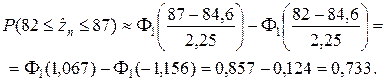
▲
– Конец работы –
Эта тема принадлежит разделу:
Теоретические основы параметрических методов обработки экспериментальных данных
На сайте allrefs.net читайте: "Теоретические основы параметрических методов обработки экспериментальных данных"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теорема Муавра-Лапласа
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов