рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Синтез четырехзвенных рычажных механизмов по положениям звеньев
Реферат Курсовая Конспект
Синтез четырехзвенных рычажных механизмов по положениям звеньев
Синтез четырехзвенных рычажных механизмов по положениям звеньев - раздел Образование, Теория механизмов и машин Четырехзвенные Механизмы Часто Применяются...
Четырехзвенные механизмы часто применяются для переноса различных предметов с позиции на позицию. При этом переносимый предмет может быть связан как с шатуном, так и с одним из звеньев, образующих кинематическую пару со стойкой.
Синтез шарнирных четырехзвенников по положениям шатуна
а) Синтез шарнирного четырехзвенника по двум положениям шатуна
Заданы два положения шатуна (рис. 2.32) с выбранными на них центрами подвижных шарниров В и С (В1С1 – первое положение, В2С2 – второе положение). Требуется определить положения центров шарниров стойки А и D, т.е. определить длины звеньев  1,
1,  3 и
3 и  0.
0.
Звенья 1 и 3, длины которых требуется определить, совершают вращательное движение, следовательно точки В и С движутся по дугам окружностей.
Соединим между собой точки В1 и В2, а также С1 и С2. Из середины полученных отрезков В1В2 и С1С2 восстановим перпендикуляры  1-1 и II-II, которые являются геометрическими местами возможных положений шарниров стойки, удовлетворяющих условиям задачи. Таким образом, эта задача имеет бесчисленное множество решений. Для
1-1 и II-II, которые являются геометрическими местами возможных положений шарниров стойки, удовлетворяющих условиям задачи. Таким образом, эта задача имеет бесчисленное множество решений. Для
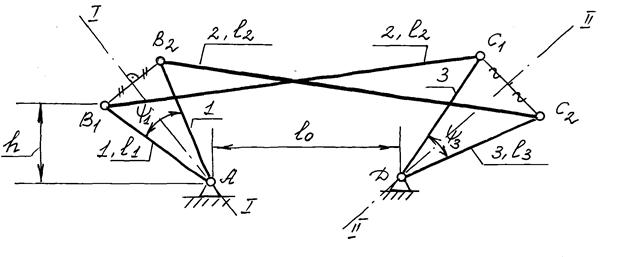
Рис. 2.32
получения определенности в решении задачи необходимо задать дополнительные условия. Это может быть, например, задание положения стойки  0 ; обеспечение заданных углов
0 ; обеспечение заданных углов 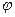 1 и
1 и  3 при перемещении шатуна 2 из положения 1 в положение 2 и т.д.
3 при перемещении шатуна 2 из положения 1 в положение 2 и т.д.
б) Синтез шарнирного четырехзвенника по трем положениям шатуна
Задано три положения (рис.2.33) шатуна 2 (В1С1, В2С2 , В3С3) с выбранными на них центрами подвижных шарниров В и С. Требуется определить длины звеньев 1,
1,  3 и
3 и  0.
0.
Рис. 2.33
Последовательность решения задачи аналогична предыдущему случаю и имеет единственное решение. Точка А лежит на пересечении перпендикуляров I-I и II-II соответственно к отрезкам В1В2 и В2В3. Положение точки D находится аналогично.
Синтез кривошипно-ползунного механизма по двум соответствующим положениям входного и выходного звена
Дано (рис. 2.34): два положения ползуна (координаты т.С: хс1 и хс2), два соответствующих им положения линии кривошипа, заданные углами 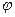 11 и
11 и 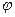 12, отсчитываемых от оси Х, параллельной оси направляющих, смещение е. Определить длины звеньев
12, отсчитываемых от оси Х, параллельной оси направляющих, смещение е. Определить длины звеньев  1 и
1 и  2.
2.
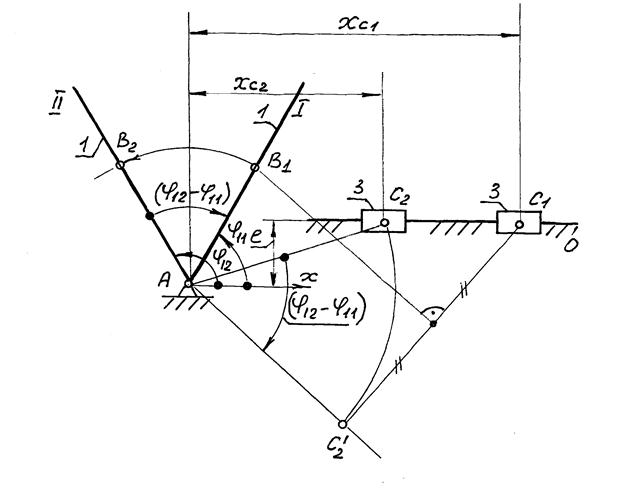
Рис. 2.34
Графическое решение задачи получаем, применяя метод обращения движения. Суть его состоит в сообщении всему механизму (включая стойку) дополнительного движения с целью остановки одного из звеньев, подвижного в действительном движении. Получаемый при этом механизме называется обращенным.
Остановим входное звено 1 в положении I. Для совмещения положения II с положением I, звено 1 необходимо повернуть на угол (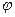 12-
12-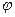 11) по часовой стрелке. При этом должно сохраниться заданное взаимное расположение звеньев, образующих в положении II фигуру IIАС2. Поэтому, принимая фигуру IIАС2 жесткой, поворачиваем ее вокруг точки А на тот же угол (
11) по часовой стрелке. При этом должно сохраниться заданное взаимное расположение звеньев, образующих в положении II фигуру IIАС2. Поэтому, принимая фигуру IIАС2 жесткой, поворачиваем ее вокруг точки А на тот же угол (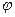 12-
12-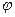 11) в том же направлении. После поворота сторона АС2 займет положение АС2′. Обе точки С1 и С2′ должны находится на одинаковом расстоянии, равном
11) в том же направлении. После поворота сторона АС2 займет положение АС2′. Обе точки С1 и С2′ должны находится на одинаковом расстоянии, равном  2, от точки В в положении 1. Поэтому точку В1 найдем как точку пересечения перпендикуляра к отрезку С1С2′, восстановленного из его середины, с линией входного звена А – I. Следовательно,
2, от точки В в положении 1. Поэтому точку В1 найдем как точку пересечения перпендикуляра к отрезку С1С2′, восстановленного из его середины, с линией входного звена А – I. Следовательно,  1=
1=  АВ1 и
АВ1 и  2=
2=  В1С1.
В1С1.
Точку В2 находим, проводя дугу через найденную точку В1 до пересечения с положением II входного звена.
Синтез четырехзвенных рычажных кривошипных механизмов по заданному ходу выходного звена. Коэффициент изменения его средней скорости
Частным случаем синтеза механизмов по положениям звеньев является синтез кривошипных механизмов по заданному ходу выходного звена. Ход звена определяется его крайними положениями, т.е. положениями, из которых оно может двигаться лишь в одном направлении. Ход может быть угловым (при возвратно-вращательном движении выходного звена) или линейным (при поступательном движении выходного звена). Положения механизма, соответствие крайним положениям выходного звена, называются крайними.
Пусть даны (рис.2.35) два крайних положения выходного звена 3, заданные углами 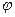 31 и
31 и 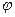 32, отсчитываемых от линии стойки, длины
32, отсчитываемых от линии стойки, длины  3 и
3 и  0. Требуется определить длины кривошипа и шатуна.
0. Требуется определить длины кривошипа и шатуна.
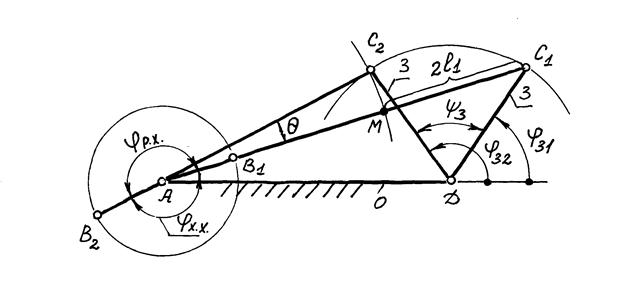
Рис. 2.35
В крайних положениях механизма кривошип и шатун располагаются на одной прямой: в одном случае они вытягиваются в одну линию, в другом - накладываются друг на друга.
Соединим между собой точку А с точками С1 и С2. В результате:
АС1=  1+
1+ 2 (а)
2 (а)
АС2=  2-
2- 1 (б)
1 (б)
Вычитая из первого уравнения второе, получим: АС1 – АС2 = 2 1. В итоге
1. В итоге
 1 = МС2/2 = (АС1 – АС2)/2.
1 = МС2/2 = (АС1 – АС2)/2.
Сложим уравнения (а) и (б). Тогда АС1 + АС2 = 2 2. В результате:
2. В результате:
 2 = (АС1 + АС2)/2
2 = (АС1 + АС2)/2
Аналогично могут быть найдены  1 и
1 и  2 графически и рассчитаны по тем же формулам для аксиального кривошипно-ползунного механизма (рис. 2.36), если заданы крайние положения ползуна, закоординированные относительно центра вращения кривошипа, и задано перемещение выходного звена.
2 графически и рассчитаны по тем же формулам для аксиального кривошипно-ползунного механизма (рис. 2.36), если заданы крайние положения ползуна, закоординированные относительно центра вращения кривошипа, и задано перемещение выходного звена.
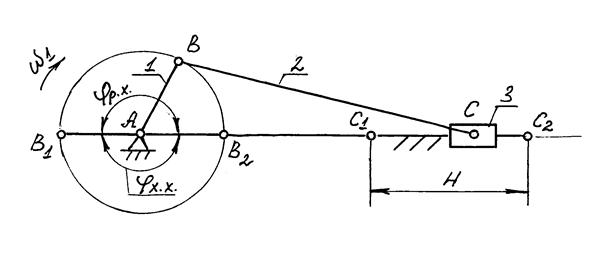
Рис. 2.36
Как видно из построения, переходу коромысла (рис.2.35) или ползуна (рис.2.36) из одного крайнего положения в другое в том и другом направлениях, т.е. при прямом (рабочем) ходе и при обратном (холостом) ходе, соответствуют разные углы поворота кривошипа.
Если кривошип вращается равномерно, то это означает, что указанные перемещения совершаются в разное время, и, следовательно, с разными средними скоростями.
При проектировании механизмов средняя скорость выходного звена при рабочем ходе определяется из технологических условий (например, для металлорежущих станков она рассчитывается по заданной скорости резания). Для повышения производительности машин холостой ход выгоднее совершать быстрее. Поэтому больший из углов поворота кривошипа, соответствующий заданному ходу, должен соответствовать рабочему ходу, а меньший – холостому ходу. Отношение средней скорости выходного звена при холостом ходе 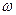 х ср к его средней скорости при рабочем ходе
х ср к его средней скорости при рабочем ходе 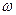 р ср. называется коэффициентом изменения средней скорости:
р ср. называется коэффициентом изменения средней скорости:
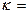
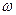 х ср /
х ср / 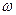 р ср.
р ср.
Так как 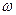 х ср=
х ср= 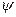 3 / tx и
3 / tx и 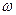 р ср=
р ср= 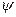 3 / tр (где tx и tp – время поворота звена соответственно на холостом и рабочем ходе), то
3 / tр (где tx и tp – время поворота звена соответственно на холостом и рабочем ходе), то 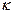 = tp / tx
= tp / tx
При равномерном вращении кривошипа
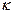 = tp/ tx =
= tp/ tx = 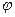 р /
р / 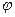 х.
х.
Аналогично для кривошипно-ползунного механизма (рис. 2.36):
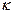 =V3ср.х../V3ср.р. = (H / tx..)/(H / tp..)= tp.. / tx. =
=V3ср.х../V3ср.р. = (H / tx..)/(H / tp..)= tp.. / tx. = 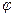 p../
p../ 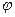 x
x
Из рис. 2.35 видно, что 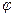 р. = 180º +
р. = 180º + 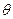 и
и 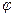 х. = 180º -
х. = 180º - 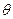 , где
, где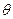 - угол смещения. Тогда
- угол смещения. Тогда
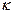 = (180º +
= (180º + 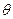 )/(180º -
)/(180º - 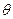 )
)
Если при синтезе задана величина коэффициента изменения средней скорости, то угол смещения определяется как
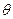 = 180º · (
= 180º · (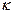 - 1)/(
- 1)/(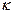 + 1)
+ 1)
а) Синтез кривошипно-коромыслового механизма по заданному ходу выходного звена и коэффициенту изменения средней скорости
Дано:  3,
3, 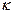 , углы
, углы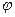 31 и
31 и 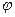 32, определяющие крайние положения выходного звена 3. Требуется определить длины звеньев 1 и 2, т.е.
32, определяющие крайние положения выходного звена 3. Требуется определить длины звеньев 1 и 2, т.е.  1 и
1 и  2.
2.
По заданному коэффициенту изменения средней скорости 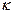 определим угол смещения
определим угол смещения 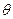 = 180º · (
= 180º · (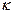 - 1)/(
- 1)/(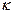 + 1).
+ 1).
Далее (рис.2.37) соединим прямой точки С1 и С2 и восстановим перпендикуляр к середине этого отрезка. Затем из т. С2 (или С1) под углом 90°-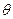 проводим прямую до пересечения с перепендикуляром, получив тем самым центр (т.О) окружности, на дугу С1С2 которой опирается центральный угол 2
проводим прямую до пересечения с перепендикуляром, получив тем самым центр (т.О) окружности, на дугу С1С2 которой опирается центральный угол 2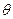 . Из точки О радиусом ОС1 или ОС2 проводим окружность и выбираем на ней в произвольном месте положение точки А. Т.к. вписанный угол С1АС2 равен половине центрального С1ОС2 , опирающегося на ту же дугу, то полученная окружность является геометрическим местом возможных положений центров вращения кривошипа (т.А), при которых будут выполняться заданные условия. Т.е. т.А можно выбирать в любом месте этой окружности и задача имеет бесчисленное множество решений. При заданной линии стойки (которая проходит через точку D) положение точки Аопределится пересечением окружности радиуса ОС1 с линией стойки и задача получает единственное решение.
. Из точки О радиусом ОС1 или ОС2 проводим окружность и выбираем на ней в произвольном месте положение точки А. Т.к. вписанный угол С1АС2 равен половине центрального С1ОС2 , опирающегося на ту же дугу, то полученная окружность является геометрическим местом возможных положений центров вращения кривошипа (т.А), при которых будут выполняться заданные условия. Т.е. т.А можно выбирать в любом месте этой окружности и задача имеет бесчисленное множество решений. При заданной линии стойки (которая проходит через точку D) положение точки Аопределится пересечением окружности радиуса ОС1 с линией стойки и задача получает единственное решение.
Длины  1 и
1 и  2 определяются по формулам, полученным выше:
2 определяются по формулам, полученным выше:
 1 = (АС1 – АС2)/2.
1 = (АС1 – АС2)/2.
 2 = (АС1 + АС2)/2
2 = (АС1 + АС2)/2
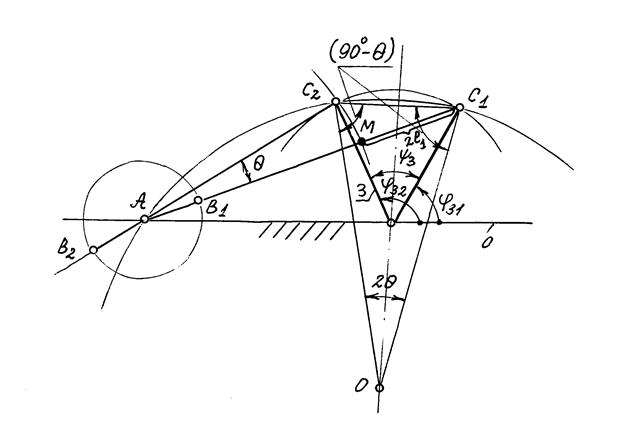
Рис. 2.37
б) Синтез кривошипно-кулисного механизма по коэффициенту изменения средней скорости
Дано: 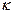 ,
,  0=
0=  АС, кулиса качающаяся (рис.2.38). Требуется определить длину кривошипа
АС, кулиса качающаяся (рис.2.38). Требуется определить длину кривошипа  1.
1.
Изобразим механизм в его крайних положениях, когда кулиса касательна к окружности радиуса  1. Из рисунка видно, что угол смещения
1. Из рисунка видно, что угол смещения 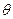 равен угловому ходу
равен угловому ходу 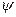 3 из условия взаимной перпендикулярности сторон. Это является особенностью данного механизма.
3 из условия взаимной перпендикулярности сторон. Это является особенностью данного механизма.
Поскольку 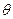 =
= 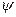 3 = 180º · (
3 = 180º · (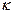 - 1)/(
- 1)/(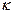 + 1), то, рассматривая прямоугольный треугольник АВ1С (или АВ2С), получим sin
+ 1), то, рассматривая прямоугольный треугольник АВ1С (или АВ2С), получим sin 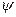 3/ 2 =
3/ 2 =  1/
1/  0, откуда
0, откуда
 1 =
1 =  0 · sin
0 · sin 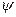 3 / 2
3 / 2
Рис. 2.38
3 Силовой (кинетостатический) расчёт плоских рычажных механизмов
Силовой расчёт выполняется на основе принципа Даламбера, согласно которому в число заданных сил включают силы инерции и моменты инерции звеньев и рассматривают равновесие полученной системы сил, используя уравнения статики. Такой расчёт носит название кинетостатического.
Задачи:
1. Определение реакций между звеньями в кинематических парах.
2. Определение уравновешивающей силы или уравновешивающего момента, т.е. такой внешней силы (или момента), которая должна действовать на заданном звене механизма, чтобы механизм при рассмотрении его по принципу Даламбера находился в равновесии.
Если сила приложена на ведущем звене, то она будет движущей. По величине этой силы можно рассчитать требуемую мощность двигателя.
Если сила приложена на ведомом звене – это сила сопротивления.
При решении задач кинетостатического расчёта вводятся следующие допущения:
1) все силы действуют в одной плоскости;
2) в первом приближении силами трения пренебрегаем.
3.1 Определение сил инерции звеньев
1) При поступательном движении звена равнодействующая сил инерции всех элементарных масс
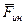 = -m·
= -m·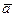 s (3.1)
s (3.1)
приложена в центре S масс звена и направлена противоположно ускорению 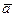 s центра S масс звена (рис. 3.1).
s центра S масс звена (рис. 3.1).
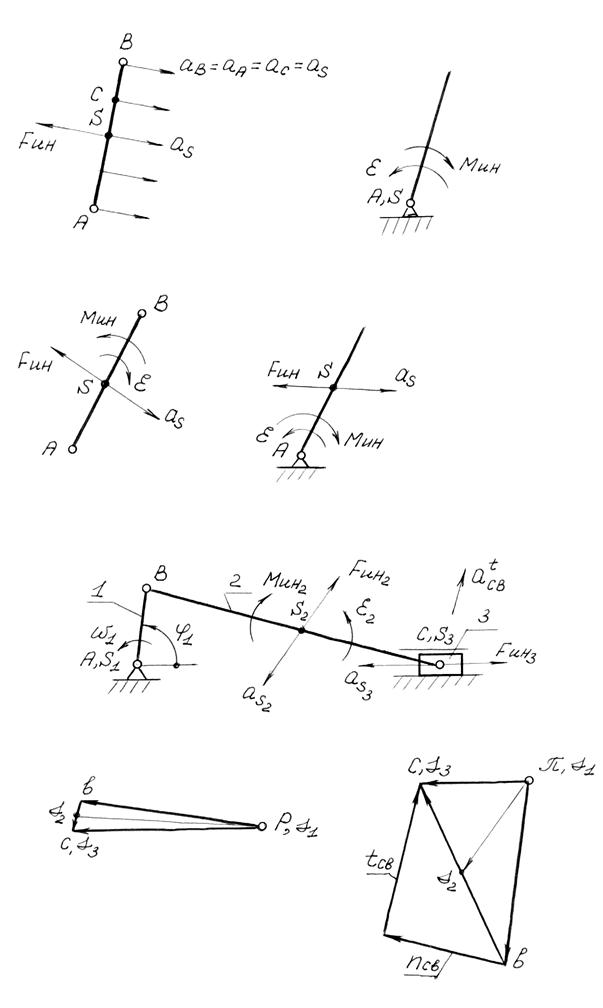
2) Если звено совершает вращательное движение вокруг оси, совпадающий с центром масс, то силы инерции всех элементарных масс можно свести к паре сил с моментом (рис. 3.2) 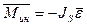 [ нм], (3.2)
[ нм], (3.2)
где JS – статический момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения.
Знак ² - ² в формуле для Мин указывает на то, что момент направлен в сторону, противоположную угловому ускорению.
Моментом инерции тела JS относительно какой-либо оси называется величина, равная сумме произведений элементарных масс этого тела на квадрат их расстояния до этой оси:
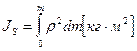 (3.3)
(3.3)
3) Звено совершает сложное движение (рис. 3.3). В этом случае движение звена раскладывается на переносное поступательное со скоростью и ускорением центра масс и на относительное вращательное движение вокруг центра масс.
Силы инерции всех элементарных масс сводятся к равнодействующей силе инерции 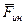 = - m·
= - m· 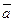 S и к паре сил с моментом
S и к паре сил с моментом 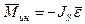 .
.
Сила инерции приложена в центре S масс звена и направлена в сторону, противоположную ускорению центра масс; момент инерции направлен в сторону, противоположную e.
4) Звено совершает вращательное движение относительно оси, не проходящей через центр масс звена (рис. 3.4).
Этот случай рассматриваем как общий случай сложного движения звена: силы инерции всех элементарных масс также сводятся к равнодействующей силе инерции 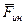 = - m ·
= - m ·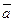 s и к паре сил с моментом
s и к паре сил с моментом 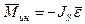 .
.
Пример. Определить Fинi и Минi для кривошипно-ползунного механизма (рис. 3.5).
Дано: w1= const, l1, l2, j1 (положение механизма определяется обобщённой координатой j1), m1, m2, m3, Js1, Js2.
Пусть центр масс 1 звена S1 находится в точке А (в центре вращения звена 1), S3 совпадает с точкой С; S2 - посередине звена 2.
Для определения Fинi и Минi надо знать линейные ускорения центров масс и угловые ускорения звеньев, для чего (при графическом решении задачи) необходимо построить планы скоростей и ускорений (рис. 3.6,а,б).
Звено 1 совершает равномерное вращательное движение (так как w1= const, то e1 = 0) . Центр масс неподвижен и аS = 0, следовательно Fин1 = 0.
Мин1 = JS1 e1 =0, так как e1 = 0 (при ω1=const).
Звено 2 совершает плоскопараллельное движение:
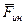 2 = - m2
2 = - m2 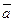 S2 ,
S2 , 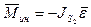 2
2
Для нахождения ускорения точки S2 воспользуемся теоремой о подобии:
BS 2 / BC = вs2 / вс; Þ вs2 = вс ВS2 / ВС
Найденный отрезок откладываем от точки в. Чтобы найти абсолютное ускорение центра масс, полученную точку s2 соединяем с полюсом плана ускорений. Тогда 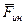 2 = -m2 (p¯s2) ма,
2 = -m2 (p¯s2) ма,
Cила инерции приложена в центре масс S2 и направлена в противоположную сторону от ускорения центра масс
|
|
|
|
|
|
Для нахождения момента инерции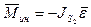 2 найдем угловое ускорение звена 2 :
2 найдем угловое ускорение звена 2 :
e2= аtСВ /lСВ = (t СВ) ма / lСВ [1 / с2 ]
Для определения направления e2 перенесем вектор тангенциальной составляющей с плана ускорений на план механизма в точку С. Этот вектор показывает направление e2; Мин2 направлен в противоположную сторону.
Звено 3 совершает поступательное движение в направляющих стойки. Сила инерции этого звена найдётся как:
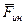 3 = - m3
3 = - m3 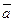 S3 = -m3 (
S3 = -m3 (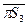 ) ма [ н ] и направлена в противоположную сторону от аS3. Мин3 = 0, так как e3 = 0.
) ма [ н ] и направлена в противоположную сторону от аS3. Мин3 = 0, так как e3 = 0.
3.2 Условие статистической определимости плоской кинематической цепи
Кинематическая цепь является статистически определимой, если число уравнений статики равно числу неизвестных при определении реакций в кинематических парах.
Для задания силы необходимы 3 параметра: точка приложения, направление, величина.
Для низших кинематических пар:
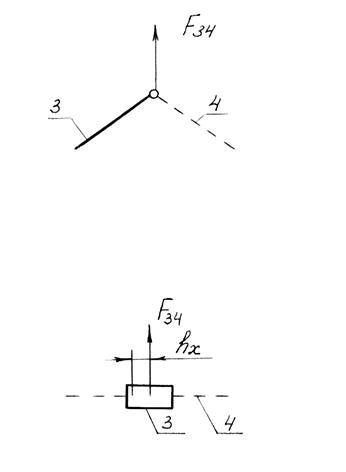
1. Вращательная пара (рис.3.7).
Звено 4 отброшено. Действие звена 4 на звено 3 заменяется реакцией F34. При этом первый индекс (в данном случае 3) – это номер звена, на которое действует реакция; второй индекс 4 – это номер звена, со стороны которого действует реакция.
Без учёта сил трения реакция во вращательной паре проходит через центр шарнира. Неизвестны величина реакции и линия её действия. Таким образом, число неизвестных при определении реакций во вращательной паре равно 2.
2. Поступательная пара (рис. 3.8).
Направляющие 4 отброшены. Без учёта трения реакция в поступательной паре перпендикулярна направляющей этой пары.
Неизвестны величина реакции и точка её приложения, т.е. имеем две неизвестных. Точка приложения определяется плечом hх относительно какой-либо точки, положение которой известно.
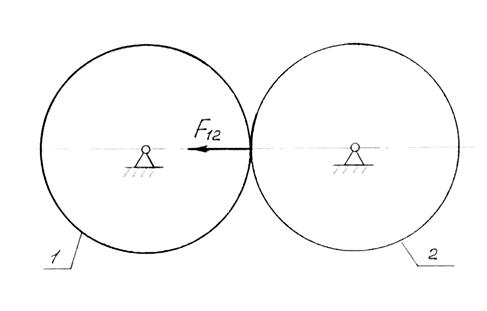
В высших кинематических парах (рис.3.9) без учёта сил трения реакция между звеньями проходит через точку касания элементов высшей пары по нормали к взаимодействующим профилям. В данном случае неизвестна одна величина – модуль реакции.
|
|
|
Таким образом, сли в кинематической цепи число низших кинематических пар составляет р1, то при определении реакций необходимо определить 2р1 неизвестных. Если цепь содержит р2 высших кинематических пар, то число неизвестных составит р2. Для каждого звена можно написать три уравнения статики: åFx = 0, åFy = 0, åMi = 0.
Если в кинематической цепи п подвижных звеньев, то число уравнений статики, которые можно написать для этой цепи, равно 3п. Чтобы кинематическая цепь была статистически определимой, необходимо выполнение условия:
2р1 + р2 = 3п
Мы рассматриваем плоские рычажные механизмы, т.е. механизмы, в которых выпшие кинематические пары (р2 = 0). В этом случае получаем равенство 3п = 2р1, которое устанавливает соотношение между числом подвижных звеньев и низших кинематических пар, при котором кинематическая цепь является статистически определима.
Это же выражение было получено при рассмотрении условия существования групп Ассура (см. раздел 1.4.3). Следовательно, группы Ассура статистически определимы.
Поэтому силовой расчёт механизма ведут по группам Ассура, начиная его с последней присоединённой группы Ассура, для которой известны все внешние силы, и заканчивают расчёт рассмотрением начального звена, на котором требуется определить уравновешивающую силу или момент.
Пример:
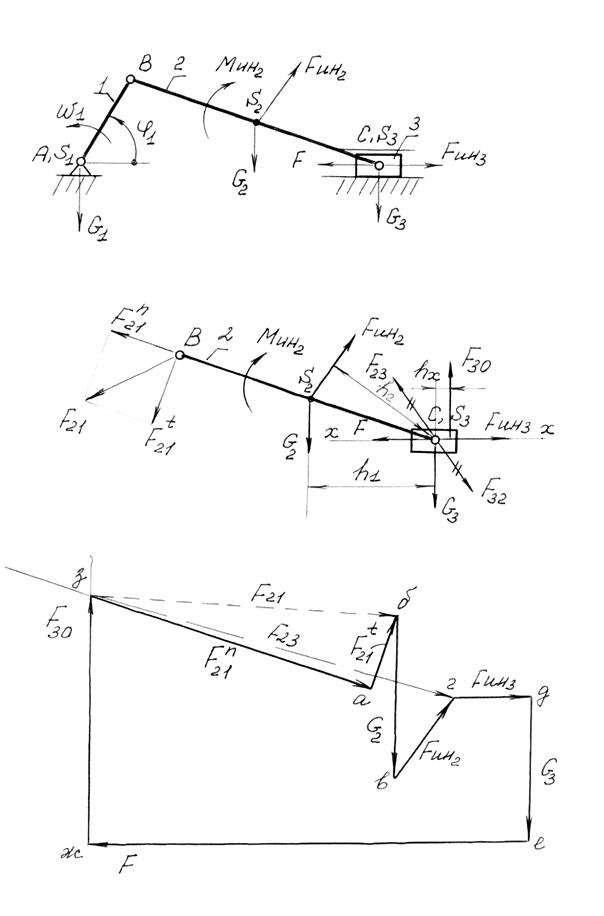
Дано: l1, l2, w1=const, j1, G1, G2, G3, Fин2, Fин3, Мин2, F (рис. 3.10).
Определить реакции во всех кинематических парах и уравновешивающую силу на кривошипе.
При силовом расчёте за начальное звено принимают звено, на котором требуется определить Fур или Мур.
Звенья 2 и 3 образуют 2ПГ Ассура 2-3 (2 вида), для которой известна внешняя сила F.
Изобразим 2ПГ Ассура 2-3 в том же положении и в том же масштабе, что и на схеме механизма. Покажем реакции F21 и F30, которые заменяют действие отброшенных звеньев 1 и 0 (рис. 3.11).
Составим таблицу, в которую будем записывать последовательность определения реакций, уравнения, которые надо составить для определения этих реакций, и номера звеньев, для которых записываются эти уравнения.
|
|
|
| Что определяем | Каким уравнением | Для какого звена |
| Ft21 | åMc = 0 | |
| Fn21 и F30 | å = 0 = 0
| 2 и 3 |
 23( или 23( или  32) 32)
| å = 0 = 0
| 2 (или 3) |
| hx | åMc = 0 |
1) Определим тангенциальную составляющую Ft21:
Ft21(ВС) ml + G2 h1 ml – Мин2 – Fин2h2ml = 0 (3.4)
 Ft21= - G2 h1 ml + Мин2+ Fин2h2ml
Ft21= - G2 h1 ml + Мин2+ Fин2h2ml
(ВС) ml
2) Для нахождения Fn21 и F30 составим векторное уравнение сил:

 å
å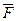 =
= 
 n21 +
n21 +  t21 +
t21 + 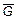 2 +
2 +  ин2+
ин2+  ин3 +
ин3 + 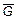 3+
3+  +
+  30 = 0 (3.5)
30 = 0 (3.5)
Выбираем масштаб для построения силового многоугольника:
mf = Ft21 / аб [ н / мм ], где аб - произвольный вектор, изображающий Ft21 в масштабе mf.
Определим отрезки, которыми будем изображать в масштабе mf остальные силы:
бв = G2 / mf [ мм ] , вг = Fин2 / mf [ мм ] и т.д.
После этого строим замкнутый (т.к. å = 0) силовой многоугольник (рис. 3.12) в той последовательности, в которой записаны силы (уравнение 3.5), в результате чего найдем векторы, изображающие искомые реакции. Величины этих реакций будут равны:
= 0) силовой многоугольник (рис. 3.12) в той последовательности, в которой записаны силы (уравнение 3.5), в результате чего найдем векторы, изображающие искомые реакции. Величины этих реакций будут равны:
Fn21 = (за) mf [ н ] и F30 = (жз) mf [ н ]
Полная реакция 21 будет складываться из ее нормальной и тангенциальной составляющих:
21 будет складываться из ее нормальной и тангенциальной составляющих:  21 =
21 =  n21 +
n21 +  t21
t21
Величина силы F21 будет равна: F21= (зб) mf [ н ]
3) Для нахождения реакции F23 составим векторное уравнение:
å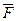 =
=  n21 +
n21 +  t21 +
t21 + 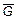 2 +
2 +  ин2+
ин2+  23 = 0 (3.6)
23 = 0 (3.6)
Первые четыре вектора в соответствии с уравнением (3.5) уже построены на рис.3.12. Поэтому для определения величины и направления силы F23 соединяем начало вектора Fn21 с концом вектора Fин2.
4) Для нахождения плеча hx составим уравнение суммы моментов относительно точки С для звена 3:
åМс = F30 hx ml = 0 (3.7)
Так как F30 ¹ 0 и ml ¹ 0, то hx = 0.
В зависимости от вида привода определяется либо уравновешивающая сила Fур , либо уравновешивающий момент Мур.
Если начальное звено приводится в движение через зубчатую передачу, то находится Fур.. Линия её действия и точка приложения определяется из рассмотрения геометрии зубчатой передачи.
В курсовом проекте условно можно принять за точку приложения силы Fур точку В кривошипа и считать, что линия действия этой силы перпендикулярна кривошипу АВ.
Если начальное звено приводится в движение через муфту, то определяется Мур.
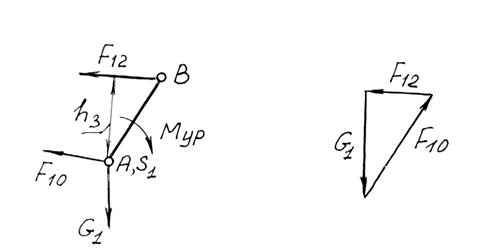
Вариант 1: Определение Fур (рис. 3.13,а).
| Fур | åM А= 0. |
 10 10
| å = 0. = 0.
|
1) åМА = Fур АВ ml - F12 ml = 0, (3.8)
откуда Fур= F12 h3 / АВ [н]
2) å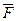 =
= 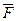 ур +
ур + 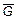 1 +
1 +  12+
12+  10 = 0 (3.9)
10 = 0 (3.9)
В соответствии с записанным уравнением строим замкнутый векторный многоугольник сил (рис.3.13,б), из которого определяем  10 .
10 .
Вариант 2: определение Мур (рис. 3.14 а,б).
| Мур | åM А= 0. |
 10 10
| å = 0. = 0.
|
1) åМА = Мур - F12 h3 ml=0 , (3.10)
откуда Мур= F12 h3 ml [н×м]
2) å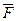 = F12+
= F12+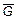 1 + 10 = 0 (3.11)
1 + 10 = 0 (3.11)
План сил для определения  10 представлен на рис.3.14,б.
10 представлен на рис.3.14,б.
3.3 Кинетостатика двухповодковых групп Ассура
Мы подробно рассмотрели кинетостатику 2ПГ 2-го вида. Теперь рассмотрим в общем виде силовой расчет остальных двухповодковых групп Ассура.
Дано: F2, F3, М2, М3 ; считаем, что в заданные силы включены силы инерции, а в моменты – моменты инерции звеньев.
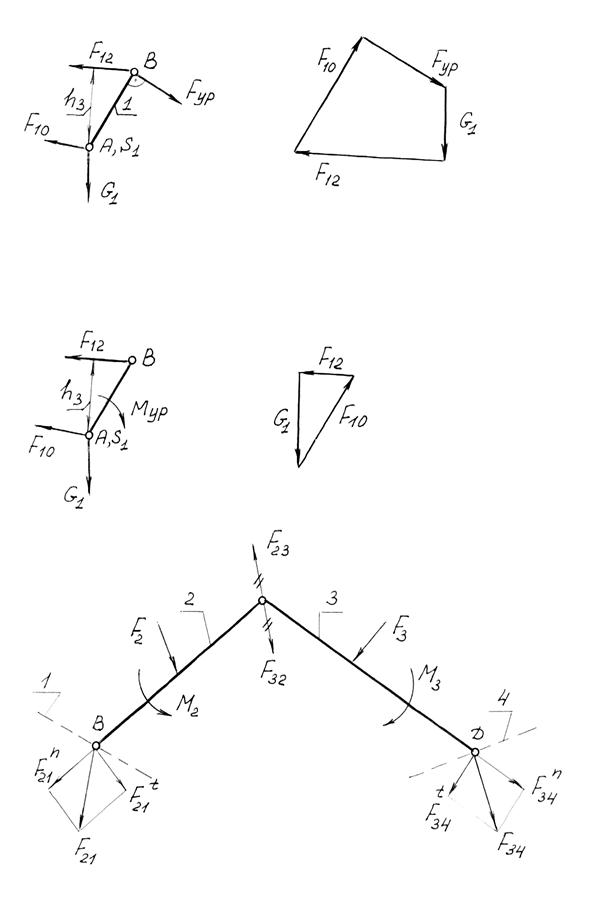
Двухповодковая группа Ассура 1 вида (рис.3.15).
Разложим силы  21 и
21 и  34 на нормальные и тангенциальные составляющие:
34 на нормальные и тангенциальные составляющие:
 21=
21=  n21 +
n21 +  t21
t21
 34=
34=  n34 +
n34 +  t34
t34
|
|
|
|
|
|
|
|
| Что определяем | Каким уравнением | Для какого звена |
| Ft21 | åMc = 0 | |
| Ft34 | åMc = 0 | |
| Fn21 и Fn34 | å = 0 = 0
| 2 и 3 |
 23 ( 23 ( 32) 32)
| å = 0 = 0
| 2 (3) |
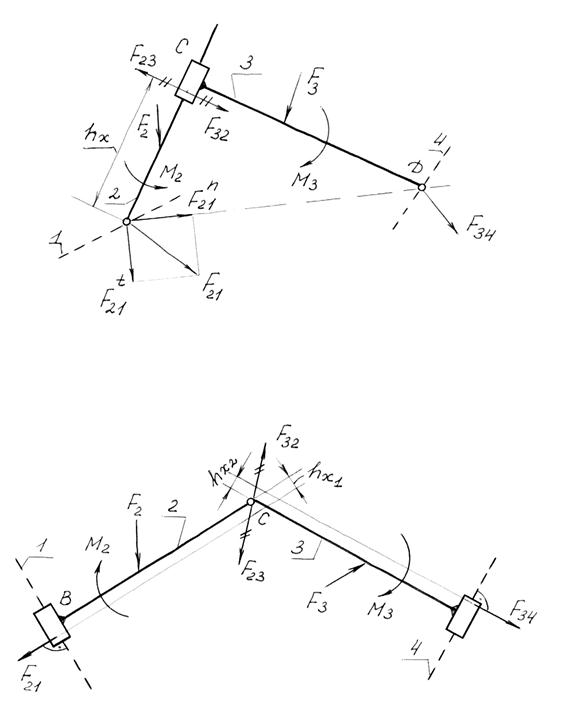
Двухповодковая группа Ассура 3 вида (рис.3.16).
| Что определяем | Каким уравнением | Для какого звена |
| Ft21 | åMD = 0 | 2 и 3 |
| Fn21 и F23 | å = 0 = 0
| |
| hx | åMB = 0 | |
| F34 | å = 0 = 0
|
Двухповодковая группа Ассура 4 вида (рис.3.17).
| Что определяем | Каким уравнением | Для какого звена |
| F21и F34 | å = 0 = 0
| 2 и 3 |
| hx1 | åMС = 0 | |
| hx2 | åMС = 0 | |
| F23 (F32) | å = 0 = 0
| 2 (3) |
Двухповодковая группа Ассура 5 вида (рис.3.18).
| Что определяем | Каким уравнением | Для какого звена |
| F32и F34 | å = 0 = 0
| |
| hx1 | åMВ = 0 | 3 и 2 |
| hx2 | åMВ = 0 | |
 21 21
| å = 0 = 0
|
3.4 Определение уравновешивающей силы с помощью рычага Жуковского
В тех случаях, когда требуется определить уравновешивающую силу или момент без предварительного определения реакций в кинематических парах, задача может быть решена с помощью рычага Жуковского.
Рычагом Жуковского называется план скоростей, повернутый на 90°, с перенесенными на него в соответствующие точки силами, и рассматриваемый как жесткий рычаг с опорой в полюсе.
Рычаг Жуковского основан на совместном применении принципов Лагранжа и Даламбера. Согласно принципу Лагранжа, если система находится в равновесии, то сумма элементарных работ всех активных сил на всяком возможном перемещении равна нулю.
|
|
|
|
|
|
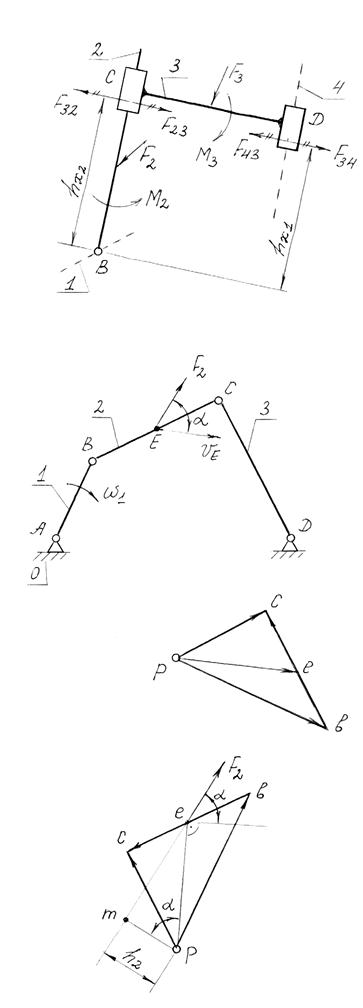
В соответствии с принципом Даламбера в число активных сил включаются силы и моменты инерции звеньев.
Возможным перемещением называется бесконечно малое перемещение допускаемое связями.
Пусть на звенья механизма действуют силы F1, F2, F3…Fn и моменты М1, М2, М3 …Мn. Причём в число заданных сил включены и силы инерции. Согласно принципу Лагранжа:
Ù
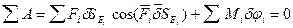 , где (3.12)
, где (3.12)
d SЕi – возможное перемещение точки приложения i-ой силы.
Ei – точка приложения i-ой силы;
dji – возможный угол поворота звена, на который действует i-ый момент.
Действительные перемещения включают в себя возможные перемещения, поэтому сумму элементарных работ можно записать в виде:
Ù
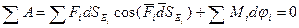
Удобнее пользоваться уравнением, в которое входят конечные величины. Для этого обе части уравнения разделим на dt. Учитывая, что d SEi / dt = VEi ; и d ji / dt = wi, получим:
Ù
åFi VЕi cos (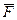 i ;
i ; 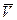 Еi) + åMi wi = åPi = 0 (3.13)
Еi) + åMi wi = åPi = 0 (3.13)
Таким образом, если механическая система находится в равновесии, то сумма элементарных мощностей åPi всех сил и моментов, действующих на систему механизма, будет равна нулю.
Знак мощности от силы определяется знаком косинуса угла между направлением силы и направлением скорости точки приложения этой силы.
Если момент и угловая скорость звена направлены в одну сторону, то мощность положительна. Если они не совпадают, то мощность отрицательна.
Учитывая, что любой момент можно представить в виде пары сил, уравнение (3.13) можно записать в следующем виде:
^
åFi VЕi cos (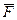 i ;
i ; 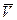 Еi) =åPi = 0
Еi) =åPi = 0
Для того, чтобы показать, как с помощью рычага Жуковского можно определить уравновешивающую силу (момент), рассмотрим вначале определение по рычагу мощности силы, используя для этого теорему о рычаге Жуковского: если система сил уравновешена на механизме, то и рычаг Жуковского под действием тех же сил, перенесённых параллельно самим себя в соответствующие точки рычага, также находится в равновесии.
Дано: условие равновесия механической системы сил, согласно принципу Лагранжа:
Ù
åFi VЕi cos (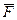 i ;
i ; 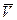 Еi) = 0 (3.14)
Еi) = 0 (3.14)
Требуется доказать, что рычаг Жуковского под действием тех же сил находится в равновесии, т.е. åМр = åFihi = 0.
Проведём доказательство на примере шарнирного четырехзвенника (рис. 3.19).
Определим с помощью рычага Жуковского мощность силы F2, действующей на звено 2:
Ù
Р (F2) = F2 V Е2 cos (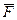 2;
2; 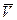 Е2) (3.15)
Е2) (3.15)
Строим план скоростей (рис. 3.20). Для нахождения скорости VЕ точки Е воспользуемся теоремой о подобии:
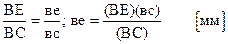 (3.16)
(3.16)
Соединив полученную точку «е» с полюсом, получим вектор скорости точки Е. Модуль скорости равен V Е= (Ре) mv [м/с].
Угол между направлением силы F2 и направлением скорости точки приложения этой силы обозначим a. Тогда
Ù
Р (F2) = F2 V Е 2cos (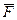 2;
2; 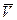 Е2) = F2 V Е2 cos a = F2 (Pe) mv cos a; (3.17)
Е2) = F2 V Е2 cos a = F2 (Pe) mv cos a; (3.17)
Построим рычаг Жуковского (рис. 3.21), повернув план скоростей на 900. Силу F2, действующую на звено 2 механизма, перенесем параллельно самой себе в соответствующую точку рычага.
Продолжим линию действия силы F2 и из полюса опустим на неё перпендикуляр. Тогда
(Pe) cos a = pm;
Р (F2) = F2 (pm) mv = F2 h2 mv, где pm = h2
F2 h2 = М (F2) – момент от силы F2. Итак, мощность любой силы с помощью рычага Жуковского можно определить как произведение момента этой силы, относительно полюса рычага на его масштабный коэффициент; причем сила должна быть перенесена параллельно самой себе в соответствующую точку рычага: Pi = mv Fi hi (3.18)
Ù
åFi VЕi cos (Fi ; VЕi) =åPi = mv åFi hi (3.19)
По условию задачи система находится в равновесии, т.е. сумма всех мощностей равна нулю: åPi = mv åFi hi = 0. Так как mv ¹ 0, то åFi hi = åМр =0, что и требовалось доказать.
Следствие: для определения уравновешивающей силы с помощью рычага Жуковского нужно все силы, действующие на звенья механизма, включая искомую уравновешивающую силу, и силы инерции звеньев, перенести параллельно самим себе в соответствующие точки рычага и приравнять нулю сумму моментов этих сил относительно полюса рычага.
На звено может действовать не только сила, но и момент.
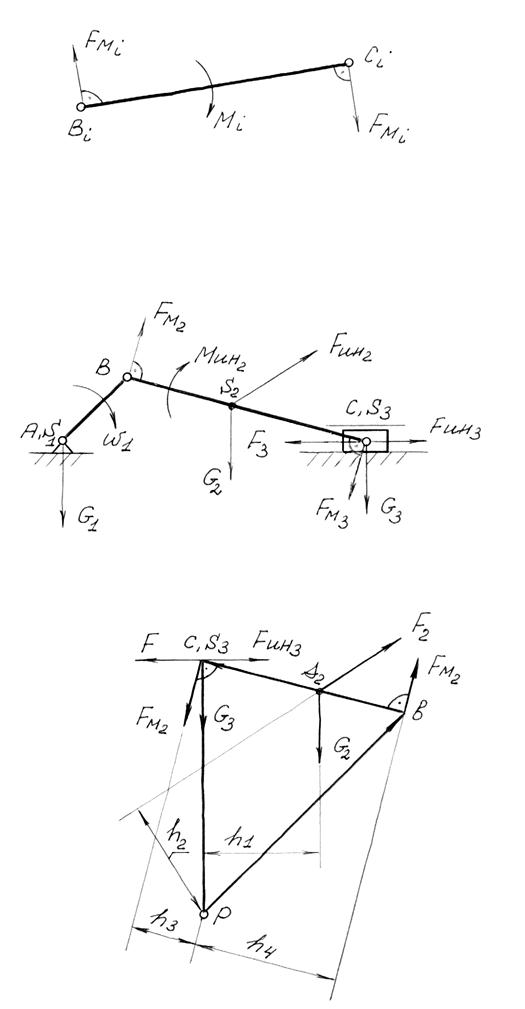
Для переноса момента на рычаг Жуковского следует представить его в виде пары сил 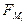 на звене (рис. 3.22). За плечо пары выбирается расстояние между двумя любыми точками на звене:
на звене (рис. 3.22). За плечо пары выбирается расстояние между двумя любыми точками на звене:
[н], (3.20)
Линия действия сил направлена перпендикулярно звену. Направление выбирается таким образом, чтобы не изменилось направление момента.
Дальнейший перенос сил производится параллельно сами себе в соответствующие точки рычага.
В качестве примера на рис. 3.24 приведен рычаг Жуковского, построенный для кривошинно-ползунного механизма (рис.3.23). Для переноса момента инерции Мин2 он был предварительно разложен на пару сил FМ2 = Мин2/lВС (рис.3.23), которые были перенесены соответственно в точки в и с рычага, параллельно самим себе (рис.3.24). После этого, из условия равновесия рычага Жуковского åМр = 0, была найдена уравновешивающая сила, действующая на кривошип:
Fур = [(F- Fин3) (рс) -G2 h1 - Fин2 h2 - + FM2 (вс)]/ (рв) [н]. (3.21)
3.5 Силовой расчет плоских рычажных механизмов с учетом трения в кинематических парах
В нашу задачу не входит подробное изложение современных теорий трения и методов расчета трущихся элементов машин. Остановимся на изложении элементарных сведений по теории трения, необходимых для решения простейших задач по ТММ (речь пойдет о сухом трении скольжения).
Формула Амонтона-Кулона (1699 г.) в ее простейшей форме имеет вид:
Fтр = f Fn, (3.22)
где f- коэффициент трения, Fn - сила нормального давления, Fтр - сила трения. Коэффициент трения зависит от состояния (обработки) трущихся поверхностей, материалов взаимодействующих тел, наличия и свойств смазки, условий работы и т.д.
|
|
|
3.5.1 Влияние трения на реакции в кинематических парах
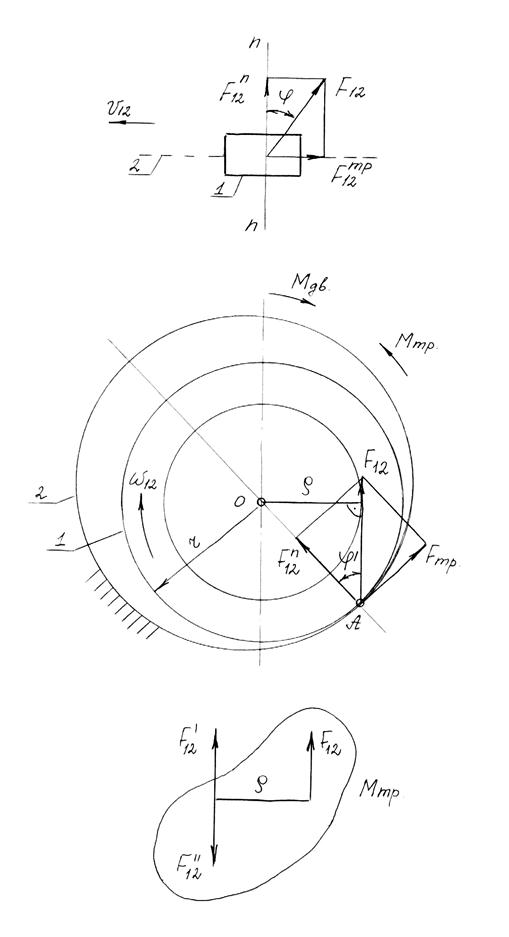
В поступательной паре (рис.3.25) полная реакция между звеньями отклоняется за счет силы трения Fтр12 от нормали n-n на угол j, называемый углом трения, в сторону, противоположную относительной скорости V12.
В кинетостатическом расчете с учетом трения удобно определять раздельно нормальную Fn12 составляющую полной реакции, обозначая ее (как и в силовом расчете без учета трения) F12, и силу трения Fтр12, учитывая их связь между собой:
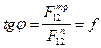 , (3.23)
, (3.23)
Fтр12 = f·F12 = F12·tgj, (3.24)
Здесь j = arctg f (3.25)
- угол трения в поступательной паре, f - коэффициент трения скольжения.
Число неизвестных при выполнении силового расчета остается прежним - это величина и точка приложения реакции.
Во вращательной паре (рис.3.26,а) вал 1 находится в опоре под действием внешнего момента Мдв и вращается с постоянной угловой скоростью w12. При вращении вала в направлении w12 при наличии трения между валом и опорой, вал будет «набегать» на опору. Предположим, что вал «набегает» на опору в точке А. Полная реакция F12 будет отклоняться от нормали на угол трения j¢. Опустим из центра вала О перпендикуляр на направление полной реакции F12 и проведем окружность радиуса r. Реакция F12 будет направлена по касательной к этой окружности, называемой кругом трения. При этом
r=r·sinj¢ (3.26)
Так как углы трения малы, то можно считать, что sinj¢»tgj¢. Тогда радиус круга трения будет приближенно равен
r=r·tgj¢=r·f¢, где (3.27)
f¢ - коэффициент трения во вращательной паре.
При силовом расчете с учетом трения удобно полную реакцию F12 переносить в центр вала О и учитывать момент (рис.3.26,б), появляющийся при таком переносе. Этот момент называют моментом трения Мтр:
Мтр=F12×r=F12·r·f¢ (3.28)
|
|
|
Коэффициент трения f¢ определяется экспериментально для различных условий работы вращательных пар и изменяется в зависимости от материалов, состояния трущихся поверхностей, от условий работы и т.п.
Как и в силовом расчете без учета трения при определении реакции между звеньями неизвестны две величины - модуль реакции и направление ее действия.
В обоих рассмотренных низших кинематических парах число неизвестных при определении реакций между звеньями с учетом трения остается таким же, как и без учета трения. Т.е. группы Ассура статически определимы и при учете трения, и силовой расчет механизма надо выполнять, разбивая его на группы Ассура.
3.5.2 Пример кинетостатического расчета кривошипно-ползунного механизма с учетом трения в кинематических парах
Уравнения, необходимые для определения реакций, действующих на звенья двухповодковой группы Ассура 2-3 (рис.3.27,б), с учетом трения в кинематических парах, будут иметь следующий вид:
1. Для звена 2:
åМс = Ft21 BC ml - F2 h2 ml - M2 - Mтр21 - Мтр23 = 0 (3.29)
2. Для звеньев 2 и 3:
å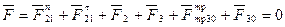 (3.30)
(3.30)
3. Для звена 2:
å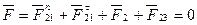 (3.31)
(3.31)
4. Для звена 3:
åМс = F30 hx ml - Mтр32 = 0 (3.32)
Моменты трения Мтр21 и Мтр23 и сила трения Fтр30, противоположны соответствующим относительным скоростям звеньев w21, w23, и V30, определяемым с помощью плана скоростей.
По предложению академика Артоболевского И.И. кинетостатический расчет с учетом трения в кинематических парах выполняется методом последовательных приближений, который заключается в следующем.
В первом приближении задача решается без учета трения, т.е. Мтр21 = Мтр23 = 0, Fтр30 = 0.
Затем по найденным реакциям определяются моменты трения в шарнирах и силы трения в поступательных парах:
Мтр21 = F12 fB rB Мтр23 = F23 fc rc Fтр30 = f30 F30, (3.33)
|
|
|
|
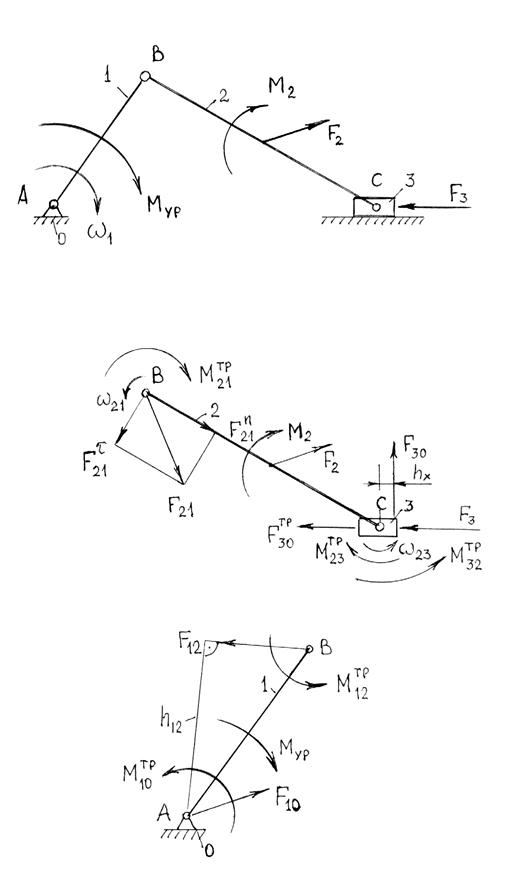
с учетом которых находятся уточненные значения реакций, т.е. выполняется второе приближение. По новым значениям сил вновь определяются моменты и силы трения и т.д.
Задача считается решенной после того, как найденные в очередном приближении реакции отличаются от предыдущих значений на требуемую величину.
Обычно ограничиваются вторым приближением.
Уравнения, необходимые для кинетостатического расчета начального звена рассматриваемого механизма с учетом трения (рис. 3.27,в) будут следующими:
1. å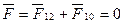 (3.34)
(3.34)
2. åМА = Мур - F12 h12 ml - Мтр12 -Мтр10 = 0, (3.35)
где Мтр12 = F21fBrB и Мтр10 = F10 fA rA. (3.26)
3.6 Коэффициент полезного действия механизмов
Под коэффициентом полезного действия (КПД) механической системы понимают отношение полезной работы к затраченной за один и тот же промежуток времени. В зависимости от промежутка времени, за который вычисляется КПД, различают цикловой и мгновенный КПД механизма
3.6.1 Цикловой КПД
Цикловой КПД механизма вычисляется за цикл установившегося движения механизма.
Работа движущих сил Адв за цикл установившегося движения расходуется на совершение работы сил полезного сопротивления Ап.с. и на совершение работы сил вредного сопротивления Ав.с., связанной с преодолением сил трения и сопротивления среды:
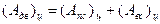 . (3.37)
. (3.37)
Цикловым КПД называется отношение:
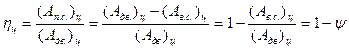 (3.38)
(3.38)
КПД показывает, какая доля работы движущих сил, подведённой к машине, полезно расходуется на совершение той работы, для которой машина создана.
Отношение y = (Ав.с)ц/ (Адв)ц (3.39) называется механическим коэффициентом потерь, который показывает, какая часть работы движущих сил, подведённая к машине, бесполезно теряется вследствие наличия трения, в конечном счёте превращаясь в теплоту. Так как потери неизбежны, то всегда
y>0. (3.40)
3.6.2 Мгновенный КПД
Кроме КПД для периода установившегося движения, дающего интегральную оценку потерь в механизме, для механизмов с одной степенью свободы вводят понятие мгновенного КПД.
Мгновенным коэффициентом полезного действия называется взятое со знаком минус отношение мощности сил полезного сопротивления к мощности движущих сил, найденное из условия статического равновесия механизма с учётом трения в кинематических парах для конкретного положения механизма.
hмгн = - Рn.с./ Рдв. (3.41)
Мгновенный КПД удобно выражать непосредственно через отношение моментов или сил. Например, для механизма, в котором ведущее и ведомое звенья совершают вращательное движение
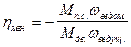 , (3.42)
, (3.42)
так как для механизма без трения
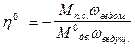 = 1,
= 1,
где М0дв. - движущий момент в механизме при отсутствии трения, то
hмгн. = М0дв./Мдв. , (3.43)
т.е. мгновенный КПД может быть определён как отношение движущего момента (или силы) без учёта трения к движущему моменту (или силы), определённому с учётом трения в механизме. При этом движущие моменты (или силы) определяются из условия статического равновесия механизма соответственно без трения и с учетом трения.
Формула удобна для вычисления, т.к. достаточно найти аналитическое выражение для момента движущих сил Мдв, а выражение для М0дв получается из него приравниванием нулю коэффициента, учитывающего трение.
3.6.3 Самоторможение
Это явление, при котором как бы велика ни была движущая сила, движение невозможно.
а) Поступательная пара (рис.3.28,а).
Если движущая сила находится внутри конуса трения, то движение невозможно, т.к. потенциально возможная сила трения всегда будет превосходить касательную составляющую от движущей силы.
б) Вращательная па
– Конец работы –
Эта тема принадлежит разделу:
Теория механизмов и машин
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Синтез четырехзвенных рычажных механизмов по положениям звеньев
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов