I II III

I – первое звено совершает вращательное движение; II– звено 2 совершает сложное движение;III– звено 3 движется поступательно.

Для определения скоростей построим план скоростей механизма (рис. 4.5). Масштабный коэффициент плана:

m_v = V_В / Рв = w₁ l₁ / Рв (4.20) Скорости:

V_S2 = (PS₂) m_v w₂ = (вс) m_v / l₂ V_С= (Рс) m_v

 

 

Рис.4.7

Рис.4.8

Рис.4.3

Рис.4.4

Рис.4.5

Рис.4.6

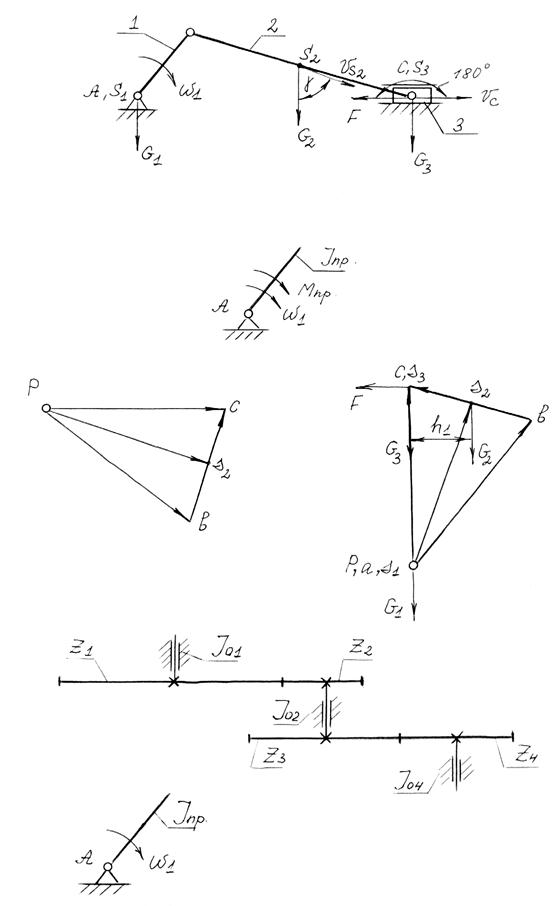
При изменении положения механизма J_пр будет меняться, т.е. J_пр является функцией положения механизма (изменяться будут (РS₂), (вс) и (Рс)).

Определим приведённый момент сил М_пр. с помощью рычага Жуковского(рис.4.6).

Мощность этого момента должна быть равна мощности всех сил, действующих на звенья механизма:

М_пр w₁ = å Р_i = m_nå F_ih_i (4.21)

или: М_пр w₁ = m_n [G₂h₂ - F(Pc)] (4.22)

Откуда М_пр = (m_n /w₁)[G₂h₂ - F(Pc)] (4.23)

 

Пример 2.

Рассмотрим зубчатую передачу (рис. 4.7).

Дано: числа зубьев колес Z₁, Z₂, Z₃, Z₄; моменты инерции колес J_s1, J_s2, J_s4.

Требуется привести массы всех звеньев к начальному звену 1,принятому за звено приведения, т.е. определить J_пр (рис.4.8).

Т зв.пр. = Т_å = åT_i = åJ_si (w²_i/2),

Т зв.пр. = Jпр w₁²/2 ; Т_å = Т₁+Т₂+Т₄ = Jпр(w²₁/2),

 

Jпр = J_s1 + J_s2 (w₂/w₁)² + J_s4 (w₄/w₁)², (4.24)

где w₂ /w₁ и w₄/w₁ - это передаточные отношения угловых скоростей колёс, равные обратному отношению радиусов или чисел зубьев колёс:

 

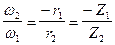, (4.25)

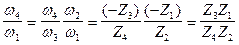, (4.26)

w₂ = w₃.

В результате:

Jпр = J_s1 + J_s2 (-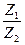)² + J_s4(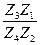)². (4.27)

В зубчатых механизмах Jпр не зависит от положения механизма, если передаточные отношения постоянны.

Таким образом, в передачах с постоянным передаточным отношением Jпр величина постоянная, не зависящая от положения механизма.

4.4 Уравнения движения машины в энергетической и дифференциальной форме

 

После приведения всех масс и сил к одному звену или к одной точке, движение механизма под действием заданных сил можно заменить движением одного звена, обладающим приведённым моментом инерции Jпр и находящимся под действием приведённого момента сил Мпр; или движением одной точки, обладающей приведённой массой m_пр и находящейся под действием приведённой силы Fпр.

Силы, действующие на звенья механизма в общем случае зависят от положения механизма, времени t и скорости V (или w).

В зависимости от удобства решения поставленной задачи используется одна из нижеприведенных форм уравнения движения.

4.4.1 Энергетическая (интегральная) форма уравнения движения машины

Обычно используется в случае, когда действующие на механизм силы зависят только от положения механизма.

а) Для звена приведения.

Так как для звена приведения кинетическая энергия в начальном и рассматриваемом положении определяются формулами Т_о = Jпр_о w₀² /2 и Т = Jпрw²/2, а сумма работ - выражением åА =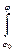Мпр dj, то уравнение движения машины Т – Т_о = åА в интегральной форме примет следующий вид:

Jпр w²/2 - Jпр_о w₀² /2 =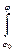Мпр dj (4.28)

Силы, действующие на звенья механизма, могут быть движущими и силами сопротивления. Соответственно для приведённого момента сил

Мпр = Мпр дв. + Мпр сопр. (4.29)

Мощность движущих сил положительна, а сил сопротивления – отрицательна, каждый момент рассматривается со своим знаком.

б) Для точки приведения.

Аналогично предыдущему случаю, учитывая что

Т= m_прV²_B/2 Т_о = m_{пр о}V²_Bо/2 åА =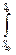Fпр dS ,

получим: Т - Т_о = åА = m_прV²_B/2 - m_{пр о}V²_Bо/2 = 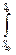Fпр dS, (4.30)

где S_B0 и S_B.- начальное и рассматриваемое положение точки В;

Fпр = Fпр дв + Fпр сопр (4.31)

4.4.2 Уравнение движения машины в дифференциальной форме

Эта форма уравнения используется, когда силы на механизме зависят не только от его положения, но и от скоростей и времени.

а) Для звена приведения.

Возьмем производные по углу поворота звена приведения для левой и правой частей уравнения (4.1):

d(T - T₀) / dj = d(åA) /dj (4.32)

Так как T₀ = const T = Jпр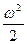 åA = 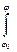Мпр dj ,

уравнение (4.32) примет вид d(T) / dj = М_пр (4.33)

Или d(J_пр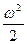)/dj = М_пр (4.34)

Учитывая, что J_пр и w величины переменные, будем иметь:

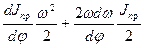= М_пр

Принимая во внимание, что 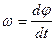, получим искомое уравнение движения машины в дифференциальной форме:

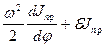= М_пр. (4.35)

Если J_пр=const, то 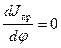и уравнение упрощается:

eJ_пр = М_пр. (4.36)

б) Для точки приведения.

Используя, как и ранее, уравнение

d(T - T₀) / dj = d(åA) /dj ,

и принимая во внимание, что в этом случае T = 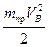, åA = 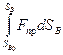, приходим к следующему уравнению движения машины в дифференциальной форме применительно к точке приведения:

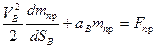(4.37)

Если m_пр=const, то 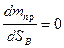, и последнее уравнение примет вид:

а_Вm_пр=F_пр. (4.38)

 

4.5 Режимы движения машины

На рис.4.9. изображена зависимость обобщенной скорости звена приведения от времени.

Различают три режима движения машины: разгон, установившееся движение, выбег.

1) Разгон - длится от момента пуска двигателя до достижения некоторого среднего значения угловой скорости звена приведения, соответствующей нормальной работе машины. При этом w₀=0, Т₀=0, Т-Т₀=åА, т.е. Т=åА. Разгон возможен в случае, когда åА_дв>½åА_сопр½.

2) Выбег - режим движения, в течение которого скорость звена приведения уменьшается до нуля: w=0, Т=0, åА_дв=0, -Т₀=åА_сопр. Пока работа сил сопротивления не израсходует всю кинетическую энергию, машина не остановится.

3) установившийся режим движения – движение, при котором обобщённая скорость является периодической функцией времени.

Циклом (периодом) установившегося движения называется период изменения обобщённой скорости, по истечении которого значение этой скорости повторяется. Для большинства машин цикл установившегося движения соответствует одному обороту кривошипа, для четырехтактных двигателей внутреннего сгорания – двум оборотам кривошипа.

В начале и в конце периода установившегося движения Т^ц = Т^ц_о, так как скорости ведущего звена в начале и в конце цикла одинаковы w=w_о, соответственно одинаковы приведённые моменты инерции в начале и в конце цикла J_ПР = J_ПРо.

Тогда: åА^ц= 0 , т.е. åА^ц_дв - ½åАс½^ц = 0

åА^ц_дв = ½åАс½^ц (4.39)

Внутри цикла установившегося движения скорость w переменна.

4.6 Причины колебания угловой скорости звена приведения внутри цикла установившегося движения

Существуют две причины колебания угловой скорости:

а) несовпадение законов изменения Мпр дв и Мпр сопр.

б) непостоянство приведённого момента инерции J_пр.

Рассмотрим каждую из причин, используя уравнение (4.40) движения машины, причём предполагаем, что вторая причина в этот момент не действует:

Jпр w²/2 - Jпр_о w₀² /2 =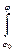Мпр dj (4.40) или Jпр w²/2 = 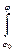Мпр dj + Т₀ , (4.41)

где Т₀ =Jпр_о w₀² /2 , Мпр = Мпр дв. + Мпр сопр.

а) Пусть Мпр дв ¹ Мпр сопр, при этом Jпр = const.

Так как Т₀ величина постоянная, то изменение угловой скорости w звена приведения объясняется изменением подъинтегральной функции, т.е. несовпадением законов изменения приведенных моментов сил движущих и сил сопротивления.

Рис.4.11

б) Приведённый момент инерции не постоянен: J_пр ¹ const.

Примем, что при этом в каждый момент времени М_пр.дв = ½М_пр.с½.

Уравнение движения машины в энергетической форме

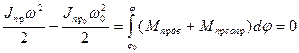
сводится к следующей форме: Jпр w²/2 = Т₀ (4.41) Изменение угловой скорости звена приведения в этом случае возможно лишь при изменении приведённого момента инерции. Там, где J_пр возрастает, w уменьшается и наоборот.

4.7 Определение угловой скорости звена приведения

Угловая скорость звена приведения находится из уравнения движения машины. При использовании уравнения движения машины в энергетической форме

,

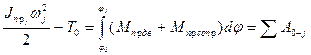получаем следующее выражение:

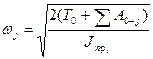(4.42)

По этой формуле можно рассчитать угловую скорость звена приведения как внутри цикла установившегося движения, так и для неустановившегося движения, в том случае, если внешние силы являются функцией положения механизма. В общем случае они могут зависеть также от скорости, и от времени, что обуславливает необходимость использования уравнения движения в дифференциальной форме.

Сложность применения уравнения (4.42) для установившегося движения состоит в том, что если не рассматривается разгон, то угловая скорость неизвестна ни в одном из положений механизма, в том числе и в начальном. Если задача решается в первом приближении, то можно считать, что w_o » w_ср = pn/30, где w_ср рассчитывается по номинальной частоте вращения «n».

Рассмотрим порядок определения угловой скорости звена приведения на примере технологической машины.

1) Для цикла установившегося движения построить ряд последовательных положений механизма.

2) Построить соответствующие рычаги Жуковского.

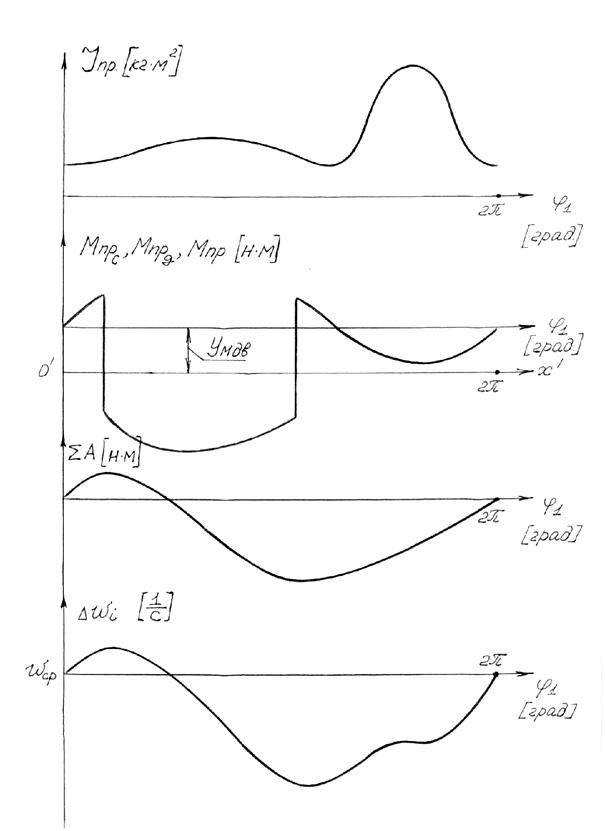
3) Используя рычаги Жуковского как планы скоростей, рассчитать кинетическую энергию и приведённый момент инерции для каждого положения механизма и построить график J_пр=J_пр(j₁) (рис.4.10):

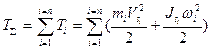, (4.43)

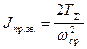, (4.44)

J_пр=J_пр.зв+J_пр.const., (4.45)

где Jпр.const – приведённый момент инерции звеньев, связанных с кривошипом постоянным передаточным отношением.

4) Для ряда последовательных положений механизма рассчитать М_{пр.сопр}. , используя рычаги Жуковского, и построить график зависимоти М_{пр.сопр} = М_{пр.сопр} (j₁) от угла поворота начального звена (рис.4.10).

5) От графика М_прс= М_прс(j₁) перейти к суммарному графику М_пр= М_пр(j).

В курсовом проекте в целях упрощения задано, что М_пр.дв = const. Графически это выражается прямой линией, отстающей от оси абцисс на ординату у_Мдв., которая неизвестна и которую требуется определить (рис.4.10).

Ординату у_Мдв определяем из условия, что за цикл установившегося движения åА^цдв = ½åА_с½^ц. Это значит, что площадь прямоугольника, ограниченная прямой М_пр.дв и осью абцисс (представляющая работу сил движущих М_пр.дв2p= у_Мдвm_м2p) должна быть равна площади фигуры, ограниченной кривой М_прс и осью абцисс (представляющая работу сил сопротивления ½åА_с½ ^ц =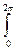М_прс dj).

Рис.4.10

Отсюда

у_Мдв= М_пр.дв./m_м = ïåА_сï ^ц /2pm_м (4.46)

Ординату у_Мдв откладываем соответственно полученному знаку.

После нахождения ординаты у_Мдв графики М_прс и М_пр.дв надо сложить, получив тем самым график суммарного приведенного момента сил. Суммарным графиком будет кривая относительно новой оси ОХ¢, смещенной относительно оси j на ординату движущего момента.

6) Рассчитать суммарную работу сил движущих и сил сопротивления и построить график изменения åА = åА(j₁) (рис.4.10):

åА = ,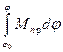

где М_пр = М_прдв + М_прс.

За цикл установившегося движения сумма работ сил движущих и сил сопротивления равна нулю, а в каждый момент времени работу определяем как площадь соответствующей фигуры.

7) Для каждого положения механизма рассчитать значения угловой скорости и построить график w_1i = w_1i (j₁) (рис.4.10):

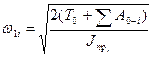, где (4.47)

Т₀ = 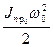, (4.48)

Jпр_о = Jпр. зв_о+ Jпр.const, (4.49)

Jпр.const – приведённый момент инерции звеньев, связанных с кривошипом постоянным передаточным отношением.

Для каждого положения механизма строим график приращения угловой скорости относительно её среднего значения w_ср: 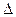w _1i = w_1i - w_ср

Для этого ось абцисс совмещаем со значением средней угловой скорости.

4.8 Коэффициент неравномерности движения машины

Определив закон движения w₁= w₁(j₁), можно определить коэффициент неравномерности движения звена приведения:

d = (w_max - w_min)/ w_ср

Для различных машин практикой эксплуатации определены допустимые значения коэффициента неравномерности:

 

Тип оборудования	коэффициент неравномерности d
Пресса Металлорежущие станки Тракторные двигатели Автомобильные двигатели Авиационные двигатели	1/5 ¸ 1/20 1/20 ¸ 1/50 1/50 ¸ 1/150 1/150 ¸ 1/300 1/300 ¸ 1/400

Если расчётный коэффициент неравномерности превышает допустимое значение, то требуется предусмотреть меры по сведению колебаний угловой скорости до допустимого значения. Для этого на валу вращающегося звена механизма устанавливают маховик.

Маховик – это тело вращения, обладающее определённым моментом инерции. Установкой маховика увеличивают кинетическую энергию всего механизма; при этом колебания кинетической энергии, оставаясь прежними по величине, будут составлять меньший процент от полной кинетической энергии механизма с маховиком. Следовательно, при этом будут уменьшаться колебания угловой скорости.

Маховик часто называют аккумулятором кинетической энергии. В тех положениях механизма, где наблюдается тенденция к увеличению угловой скорости начального звена, маховик накапливает избыточную кинетическую энергию, не давая увеличиваться угловой скорости начального звена. Там, где наблюдается тенденция к уменьшению угловой скорости, маховик отдаёт накопленную кинетическую энергию, не давая падать угловой скорости.

4.9 Определение момента инерции маховика по методу Мерцалова

Приведённый момент инерции является функцией положения механизма. Его можно представить как сумму двух слагаемых:

J_пр = J_пр.const +J_{пр зв},

где J_{пр зв} - приведённый момент инерции звеньев, связанных со звеном приведения переменным передаточным отношением,

J_пр.const – приведённый момент инерции звеньев, связанных со звеном приведения постоянным передаточным отношением. Звенья, связанные со звеном приведения постоянным передаточным отношением, выполняют ту же роль, что и маховик, обладающий моментом инерции J_мax . Назовём сумму

J_м = J_мax + J_пр.const

моментом инерции маховых масс.

При такой записи считаем, что маховик установлен на валу начального звена – звена приведения.

Тогда: J_пр = J_{пр зв}.+J_м

В соответствии с принятой записью кинетическую энергию механизма с маховиком можно представить как сумму:

Т = Т_м +Т_å,

где Т_м = J_м w²/2, Т_å= J_{пр зв} w²/2

Согласно уравнению движения машины Т= Т_о+åА, получаем

Т_м +Т_å = Т_о+åА,

или Т_м = Т_о+åА - Т_å

Изменение кинетической энергии маховых масс Т_м = J_мw²/2 при J_м = const возможно только за счёт изменения угловой скорости. При этом

Т_{м max} = (J_м w² _max)/2 = Т_о + (åА - Т_å) max,

Т_{м min} = (J_м w² _min)/2 = Т_о + (åА - Т_å) min

Максимальное приращение кинетической энергии маховых масс составит:

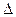Т_{м max} = J_м (w² _max - w² _min)/2 = (åА - Т_å) _max - (åА - Т_å) _min

При этом: (w² _max - w² _min )/2 = (w_max + w _min) (w _max - w_min)/2 = dw²_ср,

где (w _max + w_min )/2 = w_ср,

w _max - w_min = dw_ср.

Тогда J_мdw²_ср = (åА - Т_å) _max - (åА - Т_å) _min

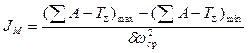(4.51)

В результате J_мах. = J_м - J_пр.const.

 

4.9.1 Последовательность определения момента инерции маховика по методу Мерцалова

Для ряда последовательных положений механизма внутри цикла установившегося движения рассчитать значение кинетической энергии механизма и построить график Т_å = Т_å(j₁) (рис.4.11). При этом учитывается кинетическая энергия звеньев механизма, связанных со звеном приведения переменным передаточным отношением. Так как w ни в одном положении не известно, то значения кинетической энергии рассчитывают приближённо по средней скорости звена приведения, определяемой по номинальной частоте вращения электродвигателя:

w » pn / 30 = w_ср.

В этом состоит приближённость метода Мерцалова.

Для каждого положения внутри цикла установившегося движения рассчитать суммарную работу движущих сил и сил сопротивления:

åА =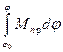

Закон изменения приведенного момента сил М_пр = М_пр(j) должен быть известен.

После этого построить график åА =åА(j₁), а затем - суммарный график [(åА - Т_å),j₁]. При этом графики (åА) и (Т_å) строятся в одинаковом масштабе (рис.4.11). Обычно за масштаб суммарного графика выбирают масштаб графика работы. По максимальному размаху графика [(åА-Т_å), j₁] рассчитывается момент инерции маховых масс (формула (4.51)), а затем и момент инерции маховика:

J_мax=J_M - J_пр.const

Если маховик установлен на валу звена приведения, то его момент берётся равным J_мax. Если он установлен на другом валу, связанном с валом звена приведения постоянным передаточным отношением, то пересчёт момента инерции производится из условия сохранения кинетической энергии:

J¢_мax (w¢)² /2 = J_маx (w²)/2, (4.52)

J¢_мax = J_мax u² , (4.53)

где u = w / w¢ - передаточное отношение,

w – угловая скорость звена приведения,

w¢ - угловая скорость звена, на котором устанавливается маховик.

Маховик выгодно устанавливать на быстро вращающемся валу, так как тот же эффект в отношении коэффициента неравномерности достигается установкой меньшего маховика.

 

 

Рис.4.12

Рис.4.11

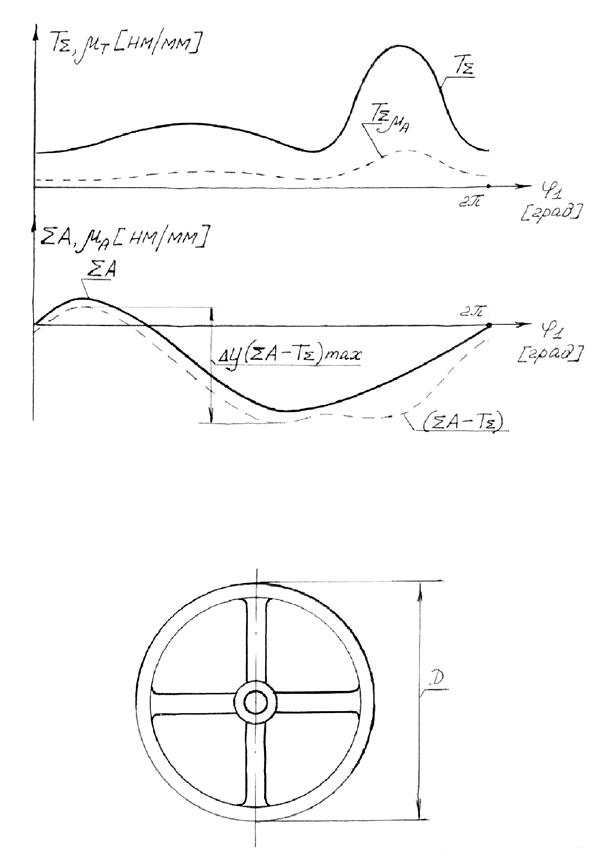
Характеристику маховика удобно задавать в форме:

mD²= [кг м²], (4.54)

где m – масса маховика, D – диаметр маховика.

Величина mD² называется маховым моментом.

Если основная масса маховика сосредоточена в его ободе, то радиус инерции маховика мало отличается от его наружного радиуса : r_ин = D/2. Тогда:

J_мax =mr²_ин = m D²/4,

откуда m D² = 4 J_мax. (4.55)

Задаваясь из конструктивных соображений диаметром обода маховика по уравнению (4.55) можно определить его массу.

Для маховика, выполненного в виде сплошного диска r_ин = D/2, J_мах = 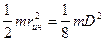и

mD² = 8J_мах. (4.56)

 

 

5 Синтез зубчатых механизмов

Зубчатые механизмы (передачи) применяются для передачи вращательного движения или для преобразования вращательного движения в поступательное и наоборот.

Из всех видов механических передач зубчатые получили наибольшее распространение из-за следующих достоинств:

- компактность,

- высокая нагрузочная способность,

- высокий К.П.Д. (до 0,99 для одной ступени),

- независимость передаточного отношения от передаваемой нагрузки.

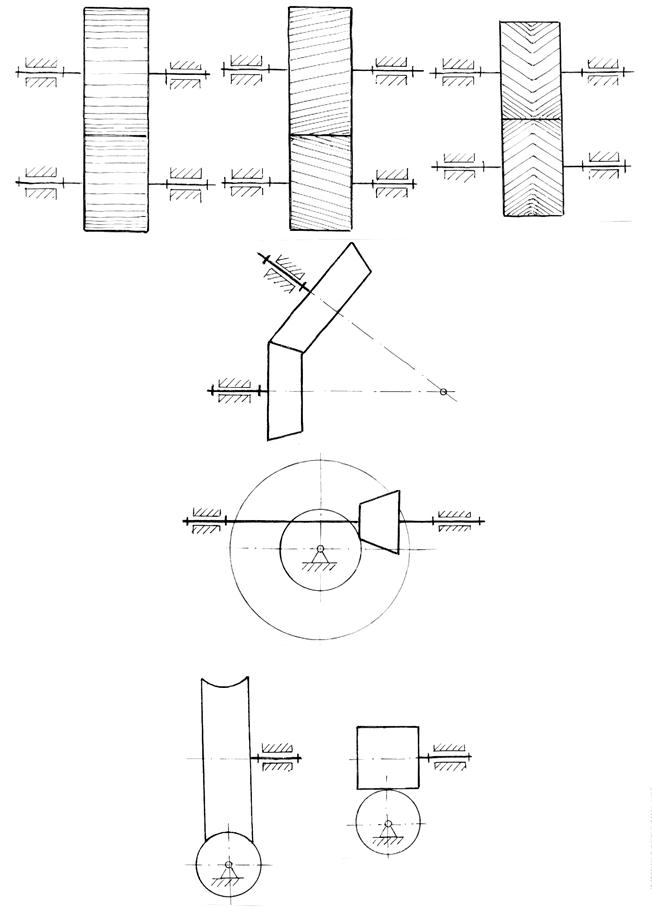
Зубчатые передачи делятся на плоские и пространственные. К плоским относятся передачи, у которых оси вращения колес параллельны (рис. 5.1,а,б,в).

У пространственных передач оси колес пересекаются (конические передачи - рис. 5.1,г) или скрещиваются (гипоидные, червячные, винтовые передачи - рис. 5.1,д,е,ж).

5.1 Основная теорема зацепления (теорема Виллиса)

Основная теорема зацепления определяет соотношение между угловыми скоростями звеньев механизма, образующих высшую кинематическую пару (к которой относится и зубчатая пара):

общая нормаль к профилям, образующим высшую кинематическую пару, проведенная в точке их контакта, делит межосевое расстояние на части (отрезки) обратно пропорциональные угловым скоростям звеньев.

Пусть звено 1 (рис. 5.2), поворачиваясь относительно оси О₁ в направлении w₁, поворачивает звено 2 относительно оси О₂ в направлении w₂.

Скорости точки «к», принадлежащей звеньям 1 и 2, будут различны по величине и по направлению:

V_k1 = w₁O₁K V_k2 = w₂O₂K (5.1)

Однако проекции этих скорости на общую нормаль n-n одинаковы (в противном случае будет наблюдаться внедрение одного профиля в другой или отрыв одного профиля от другого): V_k1ⁿ = V_k2ⁿ = V_kⁿ

или V_k1cosa₁ = V_k2cosa₂ (5.2)

С учетом (5.1): w₁O₁K cosa₁ = w₂O₂K cosa₂ (5.3)

Выполним дополнительное построение - опустим перпендикуляры на общую нормаль n-n из точек О₁ и О₂. Тогда

О₁Kcos a₁= O₁L₁ и O₂Kcosa₂ = O₂L₂,

Рис. 5.1

е) ж)

д)

г)

в)

б)

а)

 

Рис.5.3

Рис.5.2

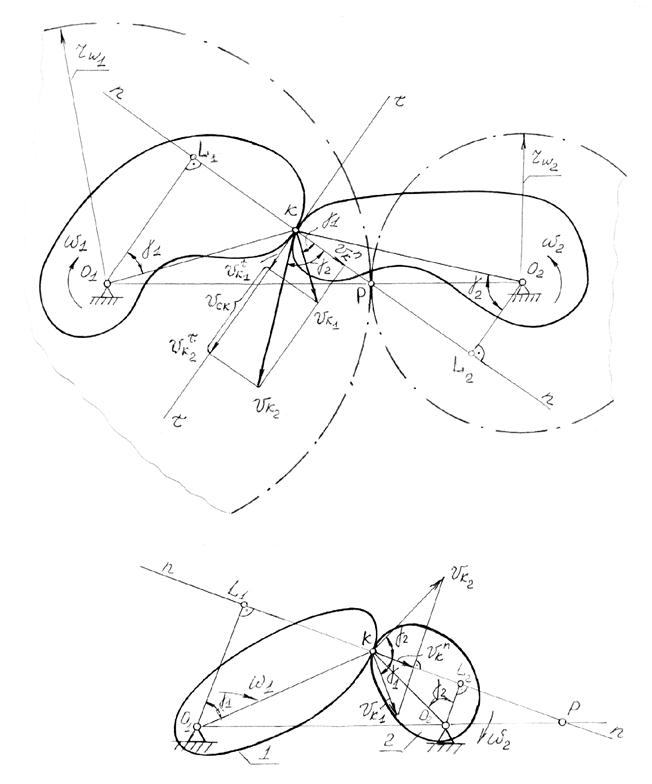
Подставляя в (5.3), получаем: w₁O₁L₁ = w₂O₂L₂, откуда

w₁/w₂ = (O₂L₂)/(O₁L₁). (5.4)

Из подобия треугольников DО₂L₂P и DO₁L₁P имеем:

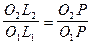(5.5)

Тогда 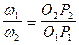(5.6)

Отношение угловых скоростей звеньев называется передаточным отношением и обозначается U₁₂ = w₁/w₂.

Точка Р - пересечение общей нормали к профилям высшей пары с межосевой линией, называется полюсом зацепления.

Рассмотренный выше случай расположения полюса Р внутри отрезка О₁О₂, когда звенья вращаются в противоположных направлениях, соответствует внешнему зацеплению звеньев. При расположении полюса зацепления вне отрезка О₁О₂ имеет место внутреннее зацепление (рис.5.3), при котором звенья вращаются в одну сторону.

Передаточное отношение считается положительным при одинаковом направлении угловых скоростей. Поскольку в первом случае они противоположны по направлению, то принято ставить знак «минус» при выражении передаточного отношения через отрезки;

U₁₂ = w₁/w₂ = - (O₂P₂)/(O₁P₁). (5.7)

При одинаковом направлении угловых скоростей:

U₁₂ = 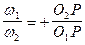. (5.8)

В общем случае можно записать:

U₁₂ = 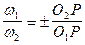. (5.9)

Передаточное отношение может быть переменным и постоянным. В передачах с переменным передаточным отношением полюс Р занимает различные положения на межосевой линиии.

Для обеспечения постоянства передаточного отношения положение полюса зацепления на межосевой линии должно быть постоянным.

Точка Р - единственная точка, в которой скорости звеньев 1 и 2 будут равны по величине и по направлению, т.е. Vp₁ = Vp₂. Из этого следует, что полюс зацепления Р является мгновенным центром вращения в относительном движении звеньев. Как известно, геометрическое место мгновенных центров относительного вращения звеньев в системе каждого из звеньев называется центроидой этого звена. При движении центроиды катятся друг по другу без скольжения. В частном случае, когда U₁₂ = const и полюс зацепления занимает неизменное положение на межосевой линии, центроидами являются окружности радиусов О₁Р и О₂Р. В зубчатых передачах они называются начальными и их параметры обозначаются с индексом «w»:

U₁₂ =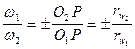. (5.10)

Проекции скоростей точки К на общую касательную t-t V_k1^t и V_k2^t определяют скорость скольжения одного профиля по другому:

V_ck = V_k2^t - V_k1^t (5.11)

5.2 Прямозубая цилиндрическая передача

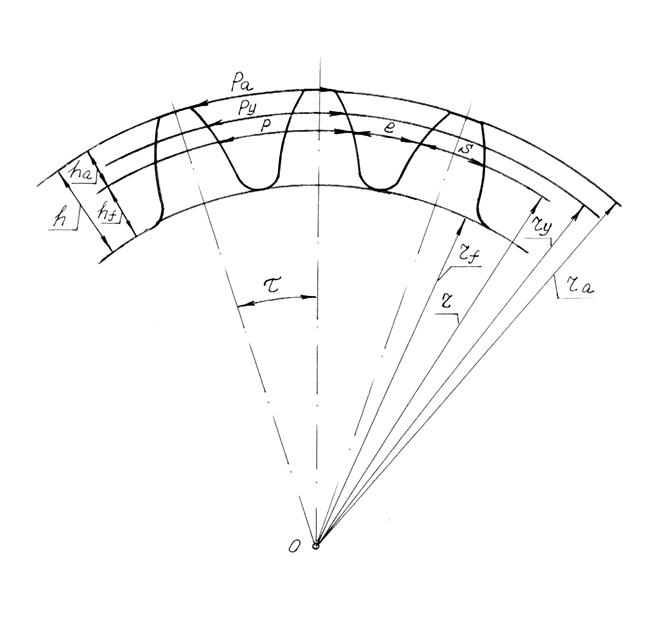
В прямозубой цилиндрической передаче линия зуба, т.е. линия пересечения боковой поверхности зуба соосной цилиндрической поверхностью - прямая, параллельная оси колеса. В прямозубой цилиндрической передаче картина зацепления одинакова во всех торцовых сечениях, т.е. сечениях, перпендикулярных осям колес, поэтому для получения представления о геометрии отдельного колеса и картины зацепления в передаче достаточно рассмотреть одно из торцовых сечений (рис.5.4), где:

r_a - радиус окружности вершин,

r_f - радиус окружности впадин,

r_y - радиус окружности произвольного радиуса,

r - радиус делительной окружности, которая является базовой для определения элементов зубьев и их размеров.

h_a - часть зуба, расположенная между делительной окружностью и окружностью вершин, называется делительной головкой зуба.

h_f - часть зуба, расположенная между делительной окружностью и окружностью впадин, называется делительной ножкой зуба,

h = h_a + h_f - полная высота зуба,

Линия пересечения боковой поверхности зуба плоскостью, перпендикулярной оси колеса, называется профилем зуба.

Расстояние между одноименными профилями (левыми или правыми) двух соседних зубьев, измеренное по дуге какой-либо окружности, называется окружным шагом, в частности:

р - окружной шаг по делительной окружности,

р_у - окружной шаг по окружности произвольного радиуса r_y.

Угловым шагом называется центральный угол, равный:

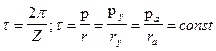, (5.12)

где z - число зубьев колеса.

Так как окружному шагу по любой окружности соответствует один и тот же угловой шаг, то это соотношение показывает, что отношение окружных шагов равно отношению радиусов соответствующих окружностей.

 

Рис.5.4

 

Определим связь между делительным окружным шагом и делительным диаметром.

Длина делительной окружности равна pd = рz. Отсюда

d = zр/p = mZ, (5.13)

где m = р/p (5.14)

- модуль колеса. Он измеряется в [мм], его значения от 0,05 мм до 100 мм стандартизированы.

Все размеры колес выражаются в долях модуля.

Окружной шаг складывается из окружной толщины зуба s и окружной ширины впадины e:

р = s + e (5.15)

В зависимости от расположения инструмента относительно оси нарезаемого колеса различают колеса без смещения (т.е. нарезанные без смещения режущего инструмента) и колеса со смещением (нарезанные со смещением режущего инструмента).

У зубчатого колеса без смещения по делительной окружности толщина зуба равна ширине впадины

S = e = р/2 = pm/2 (5.16)

Диаметр окружности вершины

d_a=2r_a=d+2h_a (5.17)

Диаметр окружности впадины

d_f=2r_f=d-2h_f (5.18)

5.2.1 Эвольвента окружности и её свойства

Существует множество кривых, обеспечивающих постоянство передаточного отношения. Однако на практике в подавляющем большинстве случаев используют эвольвентное зацепление , предложенное Эйлером, в котором боковые профили зубьев колёс выполнены по эвольвентным кривым.

Эвольвентой окружности называется траектория (кривая), которую описывает любая точка прямой, катящейся без скольжения по окружности (рис.5.5).

Все точки прямой описывают одинаковые эвольвенты, они лишь смещены друг относительно друга.

Прямая, точка которой описывает эвольвенту, называется производящей, а окружность, по которой она катится - основной.

 

Рис.5.5

Рис.5.6

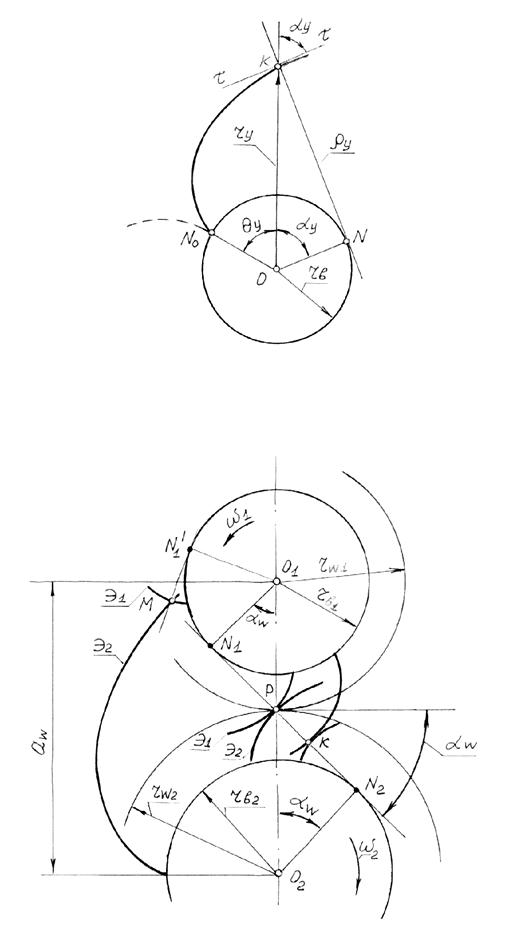
Выведем уравнения эвольвенты в параметрической форме в полярных координатах. За параметр принимаем угол профиля a_y – острый угол между касательной к эвольвенте в данной точке и радиусом вектора этой точки.

Положение любой точки эвольвенты будет определено, если будет известен текущий радиус–вектор r_y эвольвенты и полярный угол q_y (рис. 5.5), определяющий его положение. Так как производящая прямая катится по окружности без скольжения, то дуга NoN равна отрезку: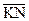

È

NoN =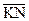 или:

r_в (q_y + a_y) = r_в tg a_y, (5.19)

где r_в - радиус основной окружности.

В результате получаем первое уравнение эвольвенты:

q_y = tga_y - a_y (5.20)

Второе уравнение эвольвенты получим, рассмотрев треугольник OKN: ОК =ОN cosa_y,

или: r_y = r_в/cosa_y (5.21)

В теории эвольвентного зацепления q_y называется инволютой угла a_у:

qy = inv a_у (5.22)

Значения функции «inv a» в зависимости от угла a представлены в виде специальных таблиц в справочниках.

Свойства эвольвенты:

1) Нормаль к эвольвенте в любой её точке совпадает с производящей прямой и касательна к основной окружности.

2) Отрезок KN является радиусом кривизны эвольвенты в точке К.

3) Эвольвента не имеет точек внутри основной окружности. Пройдя через точку возврата No, точка К производящей прямой опишет левую ветвь эвольвенты (рис.5.5).

 

5.2.2 Свойства и элементы эвольвентного зацепления

5.2.2.1 Свойства эвольвентного зацепления

1. Два эвольвентных профиля обеспечивают постоянство передаточного отношения в процессе зацепления (рис. 5.6).

2. Изменение межосевого расстояния, приводящее к изменению радиусов начальных окружностей, не влияет на передаточное отношение.

Докажем, что две эвольвенты Э₁ и Э₂ могут обеспечить постоянство передаточного отношения.

Проведём общую нормаль к эвольвентам в точке их контакта К. По первому свойству эвольвенты, она должна быть касательна к каждой из основных окружностей. Следовательно, она может занять единственное положение общей касательной N₁N₂ к двум окружностям. При вращении точка контакта К двух профилей будет менять своё положение, но всегда будет оставаться на общей нормали к профилям. Поэтому полюс зацепления Р оказывается неподвижной точкой на межосевой линии, что и является условием постоянства передаточного отношения.

Согласно основному закону зацепления:

U₁₂ = 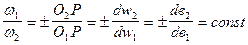(5.23)

Полученное выражение показывает, что изменение межосевого расстояния a_w, приводящее к изменению диаметров d_w1 и d_w2 начальных окружностей, не влияет на передаточное отношение. Это позволяет назначать более широкие допуски при изготовлении колёс.

3. Касание эвольвент может происходить только в пределах отрезка N₁N₂ линии зацепления (см. ниже). Точки N₁ и N₂ называются предельными точками. За предельными точками эвольвенты не имеют общей нормали и пересекаются (рис.5.6). Так, в точке М нормалью к эвольвенте Э₂ остаётся линия зацепления N₁N₂ , а нормалью к эвольвенте Э₁ является пересекающаяся с N₁N₂ прямая М N₁^/'. Это явление называется интерференцией зубьев. В зацеплении колес интерференция ведёт к заеданию и к заклиниванию передачи. При изготовлении зубчатых колес – к подрезанию зубьев, что выражается в срезании режущим инструментом части эвольвентного профиля выше основной окружности (рис.5.7) и в ослаблении зуба у основания.

 

5.2.2.2 Элементы эвольвентного зацепления

1. Линией зацепления называется траектория общей точки контакта профилей при её движении относительно стойки, т.е. прямая N₁N₂ (рис. 5.6)

2. Углом зацепления (a_w) называется острый угол между линией зацепления и перпендикуляром к межосевой линии. Угол профиля зуба в точке на начальной окружности равен углу зацепления.