Преобразования Фурье и их свойства

 

 

В этом параграфе кратко изложим необходимые для последующего сведения из теории интегральных преобразований Фурье. Подробное и полное изложение теории этих преобразований можно найти в монографии [2].

Пусть функция 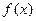действительного переменного определена на всей числовой оси и удовлетворяет следующим условиям

1. 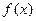является абсолютно интегрируемой, т.е.сходится.

2. на любом конечном отрезке числовой оси 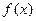не имеет бесконечного числа точек максимумов и минимумов, а также бесконечного числа точек разрыва первого ряда (т.е. точек конечных разрывов).

3. функция 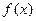не имеет разрывов второго рода.

Тогда при выполнении этих (достаточных) условий имеют место формулы

 

(10.1)

(10.2)

 

Первая формула определяет прямое преобразование Фурье, вторая – обратное. Функция 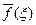называется трансформантой Фурье функции 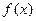. В левой части формулы (10.2) (формулы обращения) для значения , являющегося точкой разрыва функции 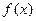нужно вместо 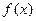писать 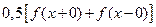. Напомним, что согласно формуле Эйлера 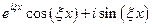, где – мнимая единица.

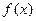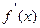Установим одно важное для приложений свойство преобразований Фурье. Пусть и удовлетворяют достаточным условиям 1 – 3 существования преобразований Фурье, тогда существуют интегралы

 

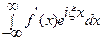и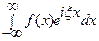

 

при всех действительных значениях параметра 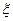, причем пр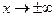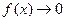и и . Применим к первому интегралу правило интегрирования по частям, получим

 

.

 

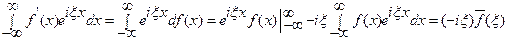Этот результат обобщается на случай применения прямого преобразования Фурье к производной :

 

(10.3)

 

Последнее равенство можно толковать так: операции дифференцирования функции 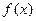(оригинала) соответствует в пространстве трансформант операция умножения трансформанты 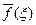на соответствующую степень . В частности, линейному дифференциальному уравнению с постоянными коэффициентами в пространстве трансформант будет соответствовать линейное алгебраическое уравнение относительно трансформанты искомой функции.

Поясним сказанное в отношении линейного дифференциального уравнения на следующем примере: требуется найти частное решение дифференциального уравнения

 

 

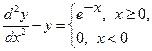
в области 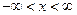, которое удовлетворяет граничным условиям 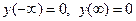. Применим прямое преобразование Фурье к обеим частям дифференциального уравнения, т.е. умножим обе части уравнения на 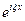, а затем проинтегрируем по переменной в пределах от 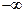до 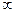. На основании формул (10.1) и (10.3) получим линейное алгебраическое уравнение относительно трансформанты .

 

.

 

Отсюда находим

.

 

При помощи формулы обращения (10.2) по известной трансформанте 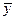определяем искомое решение дифференциального уравнения

 

.

 

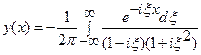Этот интеграл можно вычислить (т. е. выразить через элементарные функции) методами теории функций комплексной переменной, можно преобразовать его к сумме табличных интегралов и затем обратится к какому-либо специальному справочнику, например [5,12]. Этот путь на практике применяется наиболее часто, воспользуемся им. Умножим числитель и знаменатель подынтегральной функции на 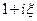, затем заменим 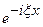согласно формуле Эйлера: , в конечном итоге представим подынтегральную функцию в виде

 

.

 

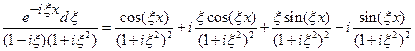Все слагаемые в правой части равенства являются интегрируемыми функциями в области . Первые два слагаемых являются четными функциями переменной интегрирования 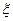, а остальные два – нечетными функциями в области . В силу этого

,

.

 

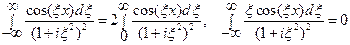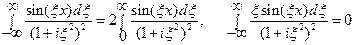Таким образом,

 

.

В справочнике [12] находим на странице 196

 

.

 

Следовательно, искомое решение дифференциального уравнения можно записать в виде

 

.

 

Непосредственной подстановкой функции 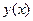в рассматриваемое дифференциальное уравнение можно убедиться, что она является его частным решением, а так как 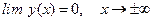, то это частное решение есть искомое.

В заключение параграфа отметим, что при помощи преобразования Фурье решения краевых задач для дифференциальных уравнений получаются в виде несобственных интегралов, которые в редких случаях удается выразить через элементарные и даже специальные функции. Основной способ получения численных результатов в этом случае базируется на методах приближенного вычисления несобственных интегралов. Некоторые из таких методов описаны в предыдущем параграфе.