рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Простейшей смешанной задачи для многослойного основания
Реферат Курсовая Конспект
Простейшей смешанной задачи для многослойного основания
Простейшей смешанной задачи для многослойного основания - раздел Образование, ДВУМЕРНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ ДЛЯ МНОГОСЛОЙНЫХ ОСНОВАНИЙ Частным Случаем Смешанной Задачи Для Многосло...
Частным случаем смешанной задачи для многослойного основания является контактная задача. Она заключается в отыскании нормальных напряжений под штампом, который вдавливается силой 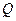 в основание (штампом принято называть абсолютно твердое тело). Ограничимся рассмотрением штампов, представляющих собой выпуклые тела вращения. Боковая поверхность любого из этих штампов – цилиндрическая. Радиус боковой поверхности будем обозначать буквой
в основание (штампом принято называть абсолютно твердое тело). Ограничимся рассмотрением штампов, представляющих собой выпуклые тела вращения. Боковая поверхность любого из этих штампов – цилиндрическая. Радиус боковой поверхности будем обозначать буквой 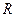 .
.
Пусть  – уравнение поверхности основания штампа, приведенного в соприкосновение с первым слоем основания. После погружения штампа на глубину
– уравнение поверхности основания штампа, приведенного в соприкосновение с первым слоем основания. После погружения штампа на глубину 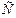 поверхность его основания будет описываться уравнением
поверхность его основания будет описываться уравнением
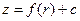 . (6.1)
. (6.1)
Пусть точка М поверхности основания, занимавшая до деформации положение 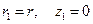 , после деформации оказалась на поверхности штампа. Ее новое положение будет характеризоваться координатами
, после деформации оказалась на поверхности штампа. Ее новое положение будет характеризоваться координатами 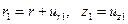 . На основании (6.1)
. На основании (6.1)
 .
.
В теории упругости смещения  и
и 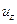 считаются весьма малыми по сравнению с наименьшим размером тела (в данном случае
считаются весьма малыми по сравнению с наименьшим размером тела (в данном случае  ). Поэтому для полного штампа
). Поэтому для полного штампа 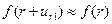 и
и 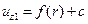
В дальнейшем считаем, что функция  непрерывна в области
непрерывна в области 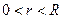 Точка
Точка  может быть угловой точкой профиля штампа. Поскольку поверхность основания штампа выпуклая, площадка контакта будет иметь форму круга. Если радиус
может быть угловой точкой профиля штампа. Поскольку поверхность основания штампа выпуклая, площадка контакта будет иметь форму круга. Если радиус  этой площадки меньше R, будем говорить о неполном погружении штампа в многослойное основание. Если
этой площадки меньше R, будем говорить о неполном погружении штампа в многослойное основание. Если 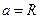 погружение штампа будем называть полным. Вне области контакта к поверхности основания никаких нагрузок не приложено. При таких предположениях относительно способа нагружения основания граничные условия задачи будут иметь вид:
погружение штампа будем называть полным. Вне области контакта к поверхности основания никаких нагрузок не приложено. При таких предположениях относительно способа нагружения основания граничные условия задачи будут иметь вид:
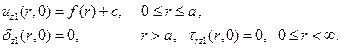
Требуется определить напряжения 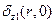 на площадке контакта.
на площадке контакта.
Заменим в граничных условиях  и
и 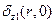 интегралами (4.6), (5.2), содержащими неизвестную функцию
интегралами (4.6), (5.2), содержащими неизвестную функцию  . Придем к парным интегральным уравнениям относительно этой функции:
. Придем к парным интегральным уравнениям относительно этой функции:
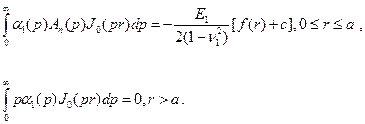 (6.2)
(6.2)
В процессе решения парных уравнений мы будем неоднократно иметь дело с перестановками различных предельных операций. Стало быть, после формального определения искомого решения необходимо, изучив его свойства, проверить, будут ли законны все указанные перестановки, и тем самым обосновать истинность формально найденного решения.
Продифференцируем обе части первого уравнения (6.2) один раз по переменной 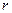 , придем к новым парным уравнениям, являющимся следствием уравнений (6.2). Попутно интеграл в левой части первого уравнения представим в виде суммы двух слагаемых, совершив замену
, придем к новым парным уравнениям, являющимся следствием уравнений (6.2). Попутно интеграл в левой части первого уравнения представим в виде суммы двух слагаемых, совершив замену  . Затем перенесем в правую часть уравнения интеграл, содержащий
. Затем перенесем в правую часть уравнения интеграл, содержащий 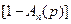 . Получим в конечном итоге
. Получим в конечном итоге
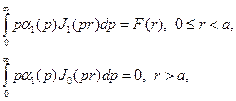 (6.3)
(6.3)
где
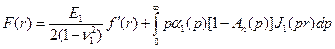 .
.
Идея решения уравнений (6.3) состоит в отыскании функции  достаточно общего вида, которая удовлетворяет одному из парных уравнений, например, второму. Затем после подстановки этой функции в другое уравнение вид ее уточняется таким образом, чтобы она удовлетворяла и этому уравнению (первому).
достаточно общего вида, которая удовлетворяет одному из парных уравнений, например, второму. Затем после подстановки этой функции в другое уравнение вид ее уточняется таким образом, чтобы она удовлетворяла и этому уравнению (первому).
На основании формулы (1.15)

убеждаемся в том, что функция 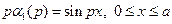 удовлетворяет второму уравнению (6.3).Функция более общего вида:
удовлетворяет второму уравнению (6.3).Функция более общего вида:
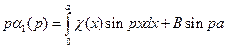 , (6.4)
, (6.4)
где 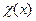 – непрерывная в области
– непрерывная в области 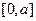 функция, а
функция, а  – произвольная постоянная, также удовлетворяет второму уравнению (6.3).В связи с этим решение парных уравнений (6.3) ищем в виде (6.4). Подставим функцию (6.4) в первое уравнение (6.3).Используя то обстоятельство, что [5]
– произвольная постоянная, также удовлетворяет второму уравнению (6.3).В связи с этим решение парных уравнений (6.3) ищем в виде (6.4). Подставим функцию (6.4) в первое уравнение (6.3).Используя то обстоятельство, что [5]

приведем первое уравнение к виду
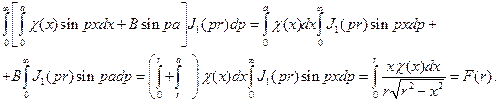
Умножим обе части последнего уравнения на 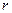 и сделаем в интеграле замену переменной
и сделаем в интеграле замену переменной 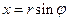 . Тогда, после замены в выражении для
. Тогда, после замены в выражении для 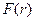 функции
функции 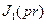 ее интегральным представлением
ее интегральным представлением
 ,
,
получим

или
 , (6.5)
, (6.5)
где
 (6.6)
(6.6)
Уравнение (6.5) является уравнением Шлемильха [6] относительно функции  . Его решение известно
. Его решение известно
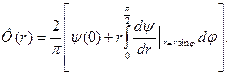
Подставив сюда  и
и 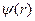 согласно (6.6), придем к интегральному уравнению относительно функции
согласно (6.6), придем к интегральному уравнению относительно функции 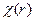 , которое после сокращения на
, которое после сокращения на 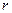 примет форму
примет форму
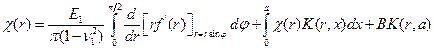 (6.7)
(6.7)
где
 .
.
Таким образом, чтобы функция (6.4) удовлетворяла первому уравнению (6.3), функция 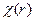 должна удовлетворять интегральному уравнению второго рода (6.7) с ядром (6.8).
должна удовлетворять интегральному уравнению второго рода (6.7) с ядром (6.8).
Выразим контактные напряжения непосредственно через функцию 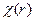 . Нормальные напряжения на верхней границе основания связаны с функцией
. Нормальные напряжения на верхней границе основания связаны с функцией  соотношением (4.6):
соотношением (4.6):
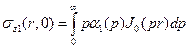 .
.
Заменим здесь  согласно (6.4), получим с помощью формулы (1.14) искомое соотношение
согласно (6.4), получим с помощью формулы (1.14) искомое соотношение
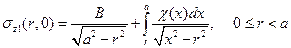 (6.9)
(6.9)
Для определения константы  в (6.9) или радиуса
в (6.9) или радиуса  площадки контакта штампа с основанием при неполном погружении штампа нужна формула, связывающая величины
площадки контакта штампа с основанием при неполном погружении штампа нужна формула, связывающая величины  и
и  с силой
с силой 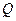 , прижимающей штамп к основанию. Из условия равновесия штампа вытекает, что
, прижимающей штамп к основанию. Из условия равновесия штампа вытекает, что
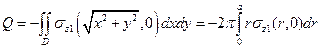 .
.
Подставим сюда вместо  правую часть равенства (6.9), получим
правую часть равенства (6.9), получим
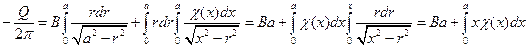 .
.
Итак,
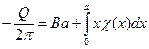 . (6.10)
. (6.10)
Формулы (6.9) и (6.10) позволяют найти решение поставленной задачи, т.е. контактные напряжения  под штампом, радиус площадки контакта
под штампом, радиус площадки контакта  при неполном погружении и константу
при неполном погружении и константу  при полном погружении. Ниже будет показано, что при неполном погружении штампа в основание
при полном погружении. Ниже будет показано, что при неполном погружении штампа в основание  .
.
Теперь нам предстоит обосновать все формально совершенные операции, которые привели к интегральному уравнению (6.7), и доказать, что формулы (6.9), (6.10) доставляют искомое решение контактной задачи.
– Конец работы –
Эта тема принадлежит разделу:
ДВУМЕРНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ ДЛЯ МНОГОСЛОЙНЫХ ОСНОВАНИЙ
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО... ОБРАЗОВАНИЯ УССР... ЗАПОРОЖСКИЙ ГОСУДАРСТВЕННЫЙ УНЕВЕРСИТЕТ ПРИВАРНИКОВ АРКАДИЙ КОНСТАНТИНОВИЧ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Простейшей смешанной задачи для многослойного основания
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов