рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- В упругой полосе при плоской деформации
Реферат Курсовая Конспект
В упругой полосе при плоской деформации
В упругой полосе при плоской деформации - раздел Образование, ДВУМЕРНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ ДЛЯ МНОГОСЛОЙНЫХ ОСНОВАНИЙ Рассмотрим Бесконечно Длинную Упругую Полосу ...
Рассмотрим бесконечно длинную упругую полосу постоянной толщины  . Материал полосы считаем однородным и изотропным. Отнесем полосу к декартовой системе координат с началом на верхней границе полосы. Ось
. Материал полосы считаем однородным и изотропным. Отнесем полосу к декартовой системе координат с началом на верхней границе полосы. Ось  направим вправо вдоль верхней границы, ось перпендикулярно оси
направим вправо вдоль верхней границы, ось перпендикулярно оси 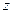 вглубь полосы. Тогда область, занятая полосой, будет характеризоваться неравенствами
вглубь полосы. Тогда область, занятая полосой, будет характеризоваться неравенствами  .
.
Задача об определении напряжений и перемещений в упругой полосе, подверженной плоской деформации сводится к определению функции напряжений  [8]. Эта функция является бигармонической, т.е. удовлетворяет бигармоническому уравнению:
[8]. Эта функция является бигармонической, т.е. удовлетворяет бигармоническому уравнению:
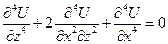 (11.1)
(11.1)
Функция напряжений связана с напряжениями 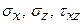 и перемещениями
и перемещениями 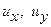 в полосе соотношениями
в полосе соотношениями
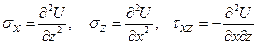 , (11.2)
, (11.2)
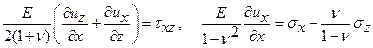 . (11.3)
. (11.3)
Здесь  – модуль Юнга материала полосы, а
– модуль Юнга материала полосы, а  – коэффициент Пуассона.
– коэффициент Пуассона.
Ограничимся рассмотрением тех задач теории упругости для полосы, в которых напряжения и функция напряжений исчезают при 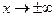 и удовлетворяют условиям существования преобразований Фурье по переменной
и удовлетворяют условиям существования преобразований Фурье по переменной  (при каждом
(при каждом 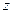 ). Умножим обе части уравнения (11.1) на
). Умножим обе части уравнения (11.1) на  и проинтегрируем по переменной
и проинтегрируем по переменной  в области
в области  , получим
, получим
 .
.
Допуская возможность перестановки операций дифференцирования по 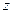 и интегрирования по
и интегрирования по  и учитывая свойство (10.3) преобразования Фурье, получим для трансформанты
и учитывая свойство (10.3) преобразования Фурье, получим для трансформанты
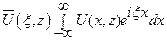
следующее дифференциальное уравнение
 .
.
При каждом значении параметра 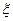 интегрального преобразования это уравнение является обыкновенным дифференциальным уравнением четвертого порядка с постоянными коэффициентами. Соответствующее ему характеристическое уравнение
интегрального преобразования это уравнение является обыкновенным дифференциальным уравнением четвертого порядка с постоянными коэффициентами. Соответствующее ему характеристическое уравнение
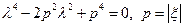
имеет кратные корни 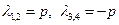 . Поэтому общее решение уравнения можно представить в виде
. Поэтому общее решение уравнения можно представить в виде
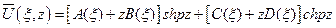 (11.4)
(11.4)
где  – произвольные функции параметра
– произвольные функции параметра 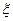 интегрального преобразования. Они должны быть подобраны так, чтобы соответствующие им напряжения и перемещения в полосе удовлетворяли заданным граничным условиям.
интегрального преобразования. Они должны быть подобраны так, чтобы соответствующие им напряжения и перемещения в полосе удовлетворяли заданным граничным условиям.
Обычно на границах полосы задаются напряжения 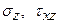 и перемещения
и перемещения 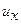 и
и  . Поэтому для дальнейшего важно установить соотношения между трансформантами напряжений и перемещений и трансформантой
. Поэтому для дальнейшего важно установить соотношения между трансформантами напряжений и перемещений и трансформантой 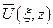 функции напряжений. Для этого умножим вначале равенства (11.2) на
функции напряжений. Для этого умножим вначале равенства (11.2) на  и проинтегрируем по переменной
и проинтегрируем по переменной  в пределах от
в пределах от 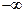 до
до 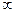 , получим
, получим
 (11.5)
(11.5)
Теперь поступим аналогично с соотношениями (11.3), придем к равенствам
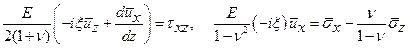 .
.
Из последнего равенства найдем 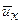 , приняв во внимание формулы (11.5) для
, приняв во внимание формулы (11.5) для  и
и 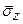
 (11.6)
(11.6)
А из предыдущего равенства определим
 . (11.7)
. (11.7)
Чтобы воспользоваться формулами (11.5), (11.6), (11.7) для определения неизвестных функций  , нужно располагать выражениями для производных по переменной
, нужно располагать выражениями для производных по переменной 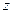 от трансформанты
от трансформанты 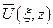 функции напряжений.
функции напряжений.
Последовательно дифференцируя равенство (11.4) по 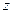 получим
получим
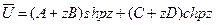 ,
,
 (11.8)
(11.8)
С учетом последних формул преобразуем равенства (11.5) – (11.7) к виду
 (11.9)
(11.9)
Как отмечалось выше на каждой границе полосы  и
и 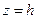 обычно задаются по две из четырех величин
обычно задаются по две из четырех величин  . Поэтому удобно перейти от неизвестных функций
. Поэтому удобно перейти от неизвестных функций  к другим неизвестным функциям, связанными с указанными напряжениями и перемещениями при
к другим неизвестным функциям, связанными с указанными напряжениями и перемещениями при  такими формулами
такими формулами
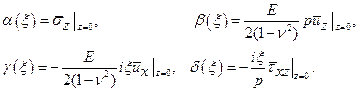 (11.10)
(11.10)
Из граничных условий на верхней границе  полосы удается определить две из четырех новых искомых функций, две другие определяются из граничных условий при
полосы удается определить две из четырех новых искомых функций, две другие определяются из граничных условий при 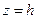 . Таким образом, число уравнений для определения функций
. Таким образом, число уравнений для определения функций  оказывается вдвое меньше, чем число уравнений для определения функций
оказывается вдвое меньше, чем число уравнений для определения функций  .
.
Выразим напряжения и перемещения в полосе непосредственно через новые искомые функции (11.10). С этой целью выразим вначале  через
через  . Положим в формулах (11.8), (11.9)
. Положим в формулах (11.8), (11.9)  и подставим получившиеся выражения для
и подставим получившиеся выражения для 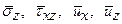 в (11.10). Придем к следующей системе уравнений относительно
в (11.10). Придем к следующей системе уравнений относительно 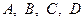 :
:
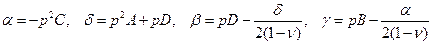 .
.
Отсюда
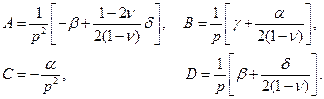
Подставим полученные выражения для величин 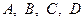 в первые две формулы (11.5), получим
в первые две формулы (11.5), получим

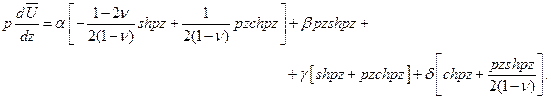
Теперь несложно выразить трансформанты напряжений и перемещений в упругой полосе непосредственно через новые искомые функции 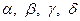 . Для этого подставим полученные выражения для
. Для этого подставим полученные выражения для 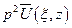 и
и 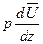 в формулы (11.9), после очевидных преобразований будем иметь
в формулы (11.9), после очевидных преобразований будем иметь



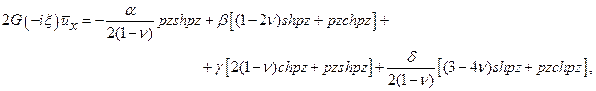
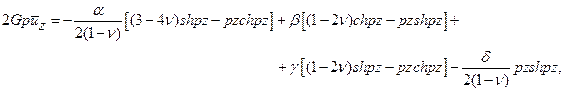 (1.11)
(1.11)
где 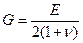 – модуль сдвига материала слоя
– модуль сдвига материала слоя 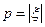 .
.
В заключение параграфа сформулируем алгоритм решения основных граничных задач для полосы, т.е. задач, в которых на верхней и нижней границах полосы задаются по две из четырех функций 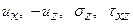 .
.
1. При помощи формулы (10.1) находим, трансформанты заданных на верхней и нижней границах полосы напряжений и перемещений.
2. При помощи формул (11.10) определяем две из четырех функций 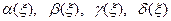 из граничных условий на верхней границе
из граничных условий на верхней границе  полосы.
полосы.
3. Полагаем в формулах (11.11) 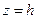 , затем в левых частях этих формул заменяем трансформанты напряжений и перемещений, теми, которые известны на нижней границе полосы, приходим к двум уравнениям относительно функций
, затем в левых частях этих формул заменяем трансформанты напряжений и перемещений, теми, которые известны на нижней границе полосы, приходим к двум уравнениям относительно функций 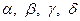 .
.
Определяем из этих уравнений две неизвестные функции из четверки функций .
.
4. Подставляем функции 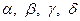 в формулы (11.11) и получаем выражения для трансформант напряжений и перемещений в упругой полосе, соответствующие рассматриваемой граничной задаче.
в формулы (11.11) и получаем выражения для трансформант напряжений и перемещений в упругой полосе, соответствующие рассматриваемой граничной задаче.
5. При помощи формулы обращения (10.2) по известным трансформантам напряжений и перемещений восстанавливаем их истинные значения.
§12 Напряженно-деформированное состояние упругой полуплоскости.
Задача Фламана
Для иллюстрации алгоритма решения граничных задач теории упругости для полосы, решим первую граничную задачу для полуплоскости  (т. е. для слоя неограниченной толщины). На границе полуплоскости
(т. е. для слоя неограниченной толщины). На границе полуплоскости  считаем заданными напряжения
считаем заданными напряжения  и
и 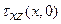 . Требуется найти в произвольной точке полуплоскости напряжения
. Требуется найти в произвольной точке полуплоскости напряжения 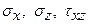 и производные перемещений
и производные перемещений 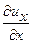 и
и  . Функции
. Функции  и
и 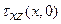 считаем абсолютно интегрируемыми в области
считаем абсолютно интегрируемыми в области  и удовлетворяющими в этой области другим достаточным условиям существования преобразования Фурье. Первое предположение приводит к заключению: при
и удовлетворяющими в этой области другим достаточным условиям существования преобразования Фурье. Первое предположение приводит к заключению: при  все искомые величины стремятся к нулю (если считать, что в ненагруженном состоянии в полуплоскости отсутствуют начальные напряжения).
все искомые величины стремятся к нулю (если считать, что в ненагруженном состоянии в полуплоскости отсутствуют начальные напряжения).
На границе  полуплоскости по условию задачи заданы напряжения
полуплоскости по условию задачи заданы напряжения  и
и 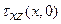 , к которым можно применить преобразование Фурье. Это позволяет по формулам (11.10) найти функции
, к которым можно применить преобразование Фурье. Это позволяет по формулам (11.10) найти функции 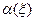 и
и  . В дальнейшем их считаем известными. По условию задачи при
. В дальнейшем их считаем известными. По условию задачи при  все искомые напряжения и производные от перемещений стремятся к нулю. Отсюда вытекает, что и трансформанты всех искомых величин также стремятся к нулю при
все искомые напряжения и производные от перемещений стремятся к нулю. Отсюда вытекает, что и трансформанты всех искомых величин также стремятся к нулю при  . Формулы (11.11) для трансформант напряжений являются линейными комбинациями функций
. Формулы (11.11) для трансформант напряжений являются линейными комбинациями функций  и
и 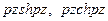 , каждая из которых при
, каждая из которых при 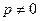 и
и  неограниченно возрастает. Однако линейные комбинации этих функций
неограниченно возрастает. Однако линейные комбинации этих функций 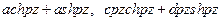 стремятся к нулю при
стремятся к нулю при  в тех случаях, когда
в тех случаях, когда 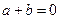 и
и  . Для доказательства этого факта достаточно воспользоваться определениями гиперболического синуса к гиперболическому косинуса
. Для доказательства этого факта достаточно воспользоваться определениями гиперболического синуса к гиперболическому косинуса  и
и  . Коэффициенты в линейных комбинациях в формулах (10.11) зависят от функций
. Коэффициенты в линейных комбинациях в формулах (10.11) зависят от функций 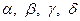 , определяющих напряженно – деформированное состояние полуплоскости. Следовательно, чтобы обеспечить стремление к нулю при
, определяющих напряженно – деформированное состояние полуплоскости. Следовательно, чтобы обеспечить стремление к нулю при  трансформант искомых величин, эти четыре функции нельзя задавать произвольно. Легко проверить, что они должны удовлетворять двум таким соотношениям:
трансформант искомых величин, эти четыре функции нельзя задавать произвольно. Легко проверить, что они должны удовлетворять двум таким соотношениям:
 (12.1)
(12.1)
Воспользуемся этими соотношениями, чтобы выразить трансформанты искомых напряжений и перемещений через известные функции 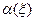 и
и  . Для этого заменим
. Для этого заменим  и
и 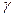 в формулах (11.11) их выражениями (12.1) через
в формулах (11.11) их выражениями (12.1) через  и
и 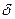 . После очевидных преобразований получим
. После очевидных преобразований получим
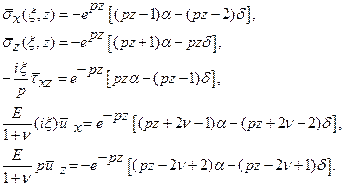
Применим теперь обратное преобразование Фурье к трансформантам искомых величин, придем тогда к формулам, которые определяют решение первой граничной задачи для упругой полуплоскости,
 (12.2)
(12.2)
Здесь
 .
.
В качестве примера, получим решение задачи Фламана об определении напряжений и производных от перемещений в упругой полуплоскости, на границу которой действует нормальная сила 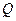 . Силу будем считать для определенности направленной вверх и приложенной в начале системы координат, к которой отнесена полуплоскость (ось направлена вглубь полуплоскости нормально к ее границе). Чтобы найти решение этой задачи, необходимо определить вспомогательные функции
. Силу будем считать для определенности направленной вверх и приложенной в начале системы координат, к которой отнесена полуплоскость (ось направлена вглубь полуплоскости нормально к ее границе). Чтобы найти решение этой задачи, необходимо определить вспомогательные функции 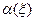 и
и  при помощи формул (12.3).
при помощи формул (12.3).
По условию задачи на границу полуплоскости  касательные нагрузки не действуют. Следовательно, во всех точках границы
касательные нагрузки не действуют. Следовательно, во всех точках границы 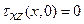 и согласно второй формуле (12.3)
и согласно второй формуле (12.3) 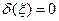 . Чтобы найти функцию
. Чтобы найти функцию  , заменим сосредоточенную силу статически эквивалентной нагрузкой, равномерно распределенной по участку
, заменим сосредоточенную силу статически эквивалентной нагрузкой, равномерно распределенной по участку 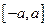 границы полуплоскости и имеющей интенсивность
границы полуплоскости и имеющей интенсивность 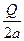 . Для распределенной нагрузки определить функцию
. Для распределенной нагрузки определить функцию  нетрудно. Если после этого перейти к пределу при
нетрудно. Если после этого перейти к пределу при  , получим функцию
, получим функцию  для случая напряжения полуплоскости нормальной сосредоточенной силой. Для нормальной нагрузки, распределено по участку
для случая напряжения полуплоскости нормальной сосредоточенной силой. Для нормальной нагрузки, распределено по участку 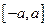 границы полуплоскости и направленной вверх, имеем
границы полуплоскости и направленной вверх, имеем
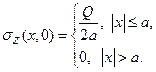
Следовательно, на основании первой формулы (12.3)
 ,
,
так как  . При
. При  получаем искомую функцию
получаем искомую функцию 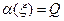 . Итак, в задаче Фламана
. Итак, в задаче Фламана  . Подставим эти функции в формулы (12.2), получим тогда решение задачи Фламана
. Подставим эти функции в формулы (12.2), получим тогда решение задачи Фламана

СПИСОК ЛИТЕРАТУРЫ
1. Т. 2 Фихт
2 Снеддон Преобр Фурье
– Конец работы –
Эта тема принадлежит разделу:
ДВУМЕРНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ ДЛЯ МНОГОСЛОЙНЫХ ОСНОВАНИЙ
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО... ОБРАЗОВАНИЯ УССР... ЗАПОРОЖСКИЙ ГОСУДАРСТВЕННЫЙ УНЕВЕРСИТЕТ ПРИВАРНИКОВ АРКАДИЙ КОНСТАНТИНОВИЧ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: В упругой полосе при плоской деформации
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов