Исследование осесимметричной деформации слоя

 

 

Рассмотрим тело вращения, отнесенное к цилиндрической системе координат (ось 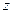направлена по оси симметрии тела).

Частным случаем такого тела является слой . Предположим, что компоненты вектора смещения 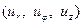не зависят от переменной 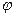. В этом случае основные соотношения теории упругости будут иметь вид [3]

 

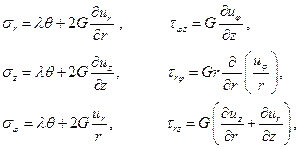(3.1)

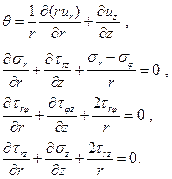(3.2)

 

Величины 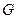и 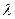связаны с модулем Юнга и коэффициентом Пуассона материала тела известными соотношениями

 

.

 

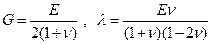Рассматриваемую деформацию тела вращения можно получить наложением двух более простых деформаций

а) ,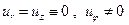

б) .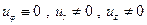

Выясним, какие напряжения возникают в теле при деформации вида а). На основании соотношений (3.1) получаем: 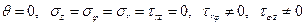. Подстановка напряжений в уравнения равновесия (3.2) позволяет легко обнаружить, что первое и третье уравнения удовлетворяются. Второе уравнение (3.2) содержит только 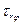и . 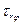Следовательно, случай деформации а) может быть реализован, например, для круглого цилиндра посредством задания на его граничных поверхностях напряжений и . Ясно, что в случае а) деформация тела вращения является деформацией кручения.

В случае деформации вида б) из соотношений (3.1) находим

 

.

 

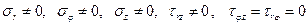Из трех уравнений равновесия (3.2) удовлетворяется второе. Поскольку первое и третье не содержат 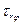и , то случай деформации б) может быть реализован, например, для круглого цилиндра заданием на граничных поверхностях последнего напряжений . Такого вида деформацию тела вращения принято называть осессиметричной деформацией.

Каждый из видов деформации типа а) и б) описывается системой уравнений более простой, чем общий случай деформации при наличии осевой симметрии. Поэтому исследование общей деформации тела вращения целесообразно сводить к исследованию двух рассмотренных видов деформации, из которых общий случай получается простым наложением соответствующих решений уравнений теории упругости. Ниже мы ограничимся случаем осесимметричной деформации тела вращения.

Между плоской и осесимметричной деформациями упругих тел имеется много общего. Как и в случае плоской деформации, напряженно-деформированное состояние тела при осесимметричной деформации зависит от двух переменных 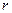и 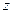, описывается двумя уравнениями равновесия (3.2) (первое и последнее уравнения). Так же как и в плоском случае напряжения можно выразить через функцию напряжений :

 

(3.3)

где

 

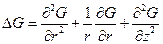. (3.4)

 

При подстановке этих напряжений в уравнения равновесия последние будут удовлетворены, какую бы функцию мы не брали.

Требуя от напряжений (3.3), чтобы они удовлетворяли условиям совместности деформаций, придем к заключению, что функция напряжений , как и в плоском случае, должна быть решением бигармонического уравнения

 

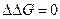. (3.5)

 

Перемещения точек тела вращения при осесимметричной деформации следующим образом связаны с функцией напряжений:

 

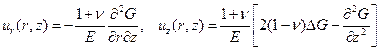. (3.6)

 

В качестве упругого тела вращения в дальнейшем будем рассматривать слой 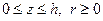, ограниченный параллельными плоскостями. Любая задача о деформации такого слоя может считаться решенной, как только для него будет найдена функция напряжений .

Рассмотрим сначала вопрос об отыскании решения бигармонического уравнения при помощи преобразования Ханкеля. С этой целью временно положим в уравнении (3.5), умножим обе части получившегося уравнения на и проинтегрируем затем по 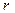. Получим

 

 

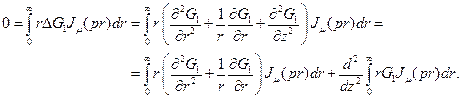
Второе слагаемое содержит трансформанту Ханкеля функции при любом . Первое слагаемое можно выразить через трансформанту Ханкеля нулевого порядка, если воспользоваться следствием (2.5) первого свойства преобразований Ханкеля. Следовательно, если взять , то первое и второе слагаемые будут выражены через одну и ту же трансформанту Ханкеля функции . В этом случае будем иметь

 

(3.7)

 

Занимаясь преобразованием правой части уравнения , мы по существу показали, что

 

. (3.8)

 

Вследствие этого уравнению (3.5) можно придать вид

 

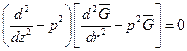
или

. (3.9)

 

В обыкновенном дифференциальном уравнении 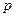– параметр, способный принимать любое значение из множества 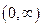. Корни соответствующего характеристического уравнения суть . Общее решение уравнения (3.9) возьмем в виде

 

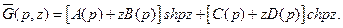(3.10)

 

Величины – произвольные функции параметра 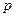. Они должны определяться из граничных условий, задаваемых на поверхности слоя. На границах слоя могут быть заданы как напряжения , так и перемещение . Для определения из граничных условий произвольных функций в решении (3.10) необходимо знать, как выражаются трансформанты Ханкеля этих напряжений и перемещений через трансформанту Ханкеля нулевого порядка 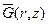. Для этого нужно применить к выражениям 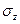и 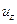в (3.3) и (3.6) преобразование Ханкеля нулевого порядка, а к функциям и преобразование Ханкеля первого порядка. Допуская возможность перестановки операций интегрирования по 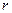и дифференцирования по 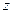и используя формулу (3.8), получаем

 

 

Привлекая еще формулу (2.6), будем иметь

 

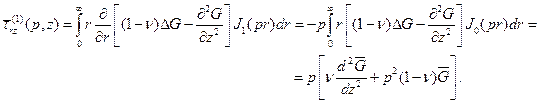
Аналогично

 

Полученным выражениям для трансформант напряжений и перемещений придадим более компактную форму, воспользовавшись тем, что

 

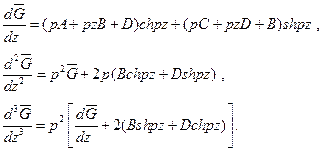(3.11)

 

С учетом этих формул

(3.12)

 

Покажем теперь, на примере конкретной граничной задачи, как определить четыре произвольные функции 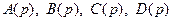в выражении (3.10) для 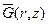. Пусть по условию при

,

при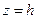

.

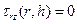Функции и 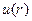считаются заданными. Предполагается, что они удовлетворяют условиям существования прямого и обратного преобразований Ханкеля.

После перехода к трансформантам в граничных условиях получим

 

 

Введем две вспомогательные функции

 

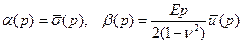, (3.13)

 

которые можно считать известными, так как известны из условия задачи , 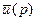. Тогда граничные условия задачи в пространстве трансформант можно переписать так:

 

 

Заменяя левые части в последних равенствах согласно формулам (3.12) и привлекая соотношения (3.11), придем к следующей системе линейных алгебраических уравнений относительно функций :

 

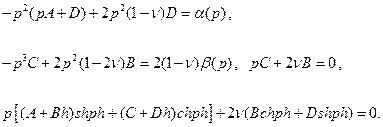(3.14)

 

Из второго и третьего уравнений системы находим

 

.

 

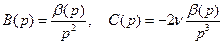Соберем в последнем уравнении члены, содержащие и 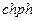. Произведем в них упрощения, используя первое и третье уравнения системы. Получим в конечном итоге

 

.

 

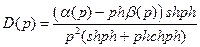Подставив 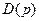в первое уравнение, найдем

 

.

 

Теперь при помощи формул (3.12) можно найти функции внутри слоя, а затем при помощи формул обращения (2.2) пр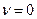и и 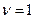сами напряжения и перемещения в слое.

Подчеркнем одно важное обстоятельство, которое вытекает из рассмотренного примера. Для определения напряженного состояния упругого гладкого слоя достаточно знать две вспомогательные функции:

 

, (3.15)

 

которые связаны с трансформантами напряжений и перемещений на верхней границе слоя.

Приведем без вывода формулы для нахождения трансформант Ханкеля напряжений и перемещений в слое по известным функциям 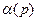и :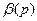

 

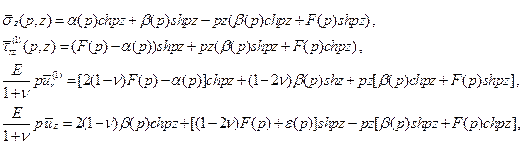(3.16)

где

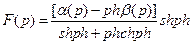. (3.17)

 

В качестве примера на использование формул (3.15), (3.16) решим задачу об определении напряжений в упругом полупространстве , нагруженном сосредоточенной силой 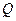. (задача Буесинеска). Сила 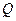приложена в точке границы полупространства и направлена так, как указано на рис. 3.1. Предполагается, что при неограниченном удалении от точки приложения силы напряжения и перемещения в полупространстве стремятся к нулю.

Упругое полупространство в этой задаче можно получить, неограниченно увеличивая толщину гладкого упругого слоя, лежащего на не деформируемом основании.

 

Рисунок 3.1 – Направление силы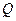

 

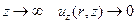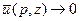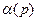Воспользуемся тем обстоятельством, что в полупространстве при . Отсюда следует, что при . А это означает, что в формулах (3.16) функции и 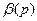должны быть связаны определенным соотношением, так как в противном случае при . Найдем вид зависимости от для упругого полупространства. Пр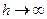и и путем замены и 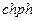в (3.17) эквивалентными бесконечно большими величинами

 

 

для упругого полупространства получим

 

.

 

Подставим 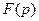в последнюю формулу (3.16) и приведем ее к виду

 

.

 

При правая часть последнего равенства стремится к нулю лишь при выполнении условия

 

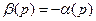. (3.18)

 

Это и есть искомое соотношение между функциям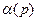и и .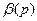

С учетом этого соотношения и полученного выше выражения для 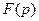можно существенно упростить формулы (3.16) для упругого полупространства и записать их в виде

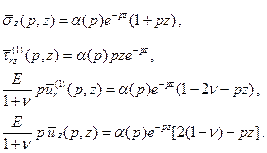(3.19)

 

Как следует из формул (3.19), решение любой граничной задачи для упругого полупространства с гладкой верхней границей сводится к отысканию одной вспомогательной функции .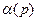

Определим 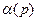для рассматриваемого случая нагружения полупространства. Если заменить сосредоточенную силу 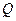равномерно распределенной по кругу нормальной нагрузкой , то для точек границы полупространства можно написать

 

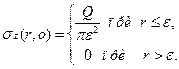
Соответствующую этим напряжениям функцию 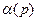получим при помощи первой формулы (3.15)

.

 

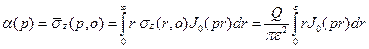Сделаем замену переменных 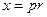в последнем интеграле и воспользуемся легко проверяемым при помощи формул (1.8), (1.9) тождеством

 

.

 

Тогда

.

 

При описанная выше распределенная нагрузка будет стремиться к заданной сосредоточенной, а найденная функция 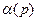к искомой функции. Таким образом, для случая сосредоточенной силы 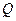будем иметь

 

.

 

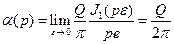Подставим полученную функцию 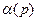в формулы (3.19) для трансформант напряжений и перемещений в упругом полупространстве, получим

 

 

Искомые напряжения и перемещения в полупространстве найдем после применения к найденным трансформантам соответствующих обратных преобразований Ханкеля

 

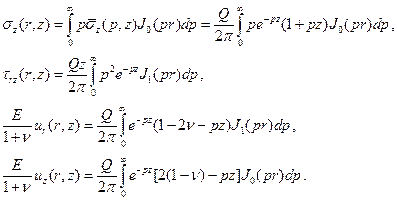
Интегралы в правых частях этих равенств могут быть выражены через элементарные функции. Для этого нужно несколько раз продифференцировать по 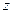обе части последнего равенства (1.16), чтобы получить необходимые для достижения цели выражения интегралов

 

через элементарные функции. Кроме того, нужно воспользоваться равенством

 

 

чтобы получить из него дифференцированием по 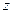соответствующие выражения для интегралов

 

В конечном итоге можно получить такие формулы для напряжений и перемещений в упругом полупространстве

 

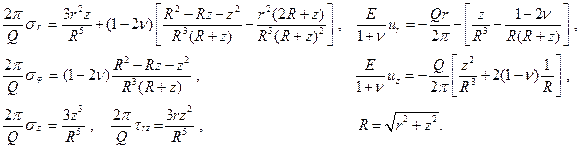(3.23)