Предмет теорії ймовірностей
Вступ
Ще зовсім недавно у природничих та технічних дисциплінах в основному застосовувалися класичні розділи математики, такі як диференціальне та інтегральне числення, диференціальні рівняння. Але останні десятиріччя істотно змінився стан справ. Ймовірно-статистичні методи глибоко проникнули у такі науки як фізика, військова справа, теорія інформацій, теорія надійності, статистичний контроль якості продукції, будівельна механіка корабля, медицина, психологія і т. п.
Предмет теорії ймовірностей
Домовимося такі поняття як дослід, експеримент, спостереження, вимір і т. п. об'єднати одним терміном випробування. Результатом випробування є деяка… Приклад. Кидання монети – випробування, випадіння герба чи числа – подія.… Події, які ми спостерігаємо, можна поділити на три види: вірогідні, неможливі і випадкові.У двох попередніх прикладах не можна передбачити, що відбудеться у кожному з цих випробувань. Та теорія ймовірностей і не ставить перед собою задачу вивчати поодинокі явища. Вона не спроможна зробити це.
Але, якщо монету підкидати достатньо велику кількість разів (декілька тисяч), то можна стверджувати, що приблизно половину разів випаде "герб", а половину – цифра.
З'являється вже деяка закономірність у випадкових однорідних випробуваннях.
Наведемо ще такий приклад. Важко сказати, хто народиться у даному конкретному випадку – хлопчик чи дівчинка. Але спостереження показали, що в усьому світі на кожні 1000 народжень припадає 514 хлопчиків. Знову з'являється закономірність у масових однорідних явищах.
Отже, предметом теорії ймовірностей є вивчення закономірностей масових однорідних випадкових подій.
Знання закономірностей, яким підкоряються випадкові події, дозволяє передбачувати, як ці події будують відбуватися у подальшому.
ЧАСТИНА І.
ВИПАДКОВІ ПОДІЇ.
ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ ЙМОВІРНОСТЕЙ
1.1. Класифікація випадкових подій і безпосередній підрахунок ймовірності
Дві події називаються несумісними, якщо в результаті випробування поява однієї з них виключає появу іншої.
Декілька подій називаються несумісними у даному випробуванні, якщо поява однієї з них виключає появу решти.
Приклади
1. Якщо виготовлена деталь, то вона може бути стандартною або нестандартною. Ці дві події несумісні. 2. Кидаємо гральний кубик. Одноразове випадання цифр 1, 2, 3, 4, 5 і 6 – події… Події у деякому випробуванні називаються рівноможливими (рівноймовірними), якщо в силу симетрії випробування жодна з…Р(А)= 3/4.
Відносна частота подій та її стійкість
Як було встановлено, формула (1) математичної ймовірності справедлива для елементарних подій, яким властиві якості випадків: вони утворюють повну… Однак, більшість задач до схеми випадків не зводиться. Події, які у них… У таких задачах використовується так звана статистична ймовірність або відносна частота події, які встановлюються із…Основні теореми теорії ймовірностей
Алгебра подій
Означення 1.Сумою або об'єднанням подій А і В називається подія С, яка полягає в появі або події А, або події В, або подій А і В разом. Інакше: подія С полягає в появі хоча б одного із подій А чи В. Позначається: С… Сумою декількох подій А1, А2,...,Аn називається подія С, яка полягає в тому, що відбувається хоча б одна з цих…Елементи комбінаторики
Комбінаторику використовують не тільки у теорії ймовірностей, але й при розв'язуванні задач економіки, теорії обчислювальних машин тощо. Правило добутку.Якщо компоненту х1 рядка (х1, х2,...,хk) можна вибрати n1…Теорема добутку ймовірностей
Введемо поняття незалежних і залежних подій. Подія А називається незалежною від події В, якщо ймовірність події А не залежить від того, відбулася… Подія А називається залежною від події В, якщо ймовірність події А залежить… Ймовірність події В, яку обчислюють при умові, що подія А відбулася, називаютьумовноюі позначають Р(В/А).Ймовірність події А до того, як стало що-небудь відомо про подію В, тобто Р(А)=7/10. Якщо стало відомо, що подія В відбулася, то Р(А/В)=6/9, з чого робимо висновки, що подія А залежить події В.
Як бачимо, умову незалежності події А від події В можна записати у вигляді :
Р(А) = Р(А/В),
а умову залежності – у вигляді :
Р(А) ¹ Р(А/В).
| Теорема добутку ймовірностей. | Ймовірність добутку двох подій дорівнюєдобутку ймовірності однієї з них на умовну ймовірність іншої, обчислену при умові, що перше мало місце: Р(АВ)=Р(А)Р(В/А). |
Доведення:
Доведемо теорему для схеми випадків. Нехай маємо n випадків, несумісних між собою, рівноможливих і таких, що утворюють повну групу подій. Зобразимо їх у вигляді n точок.
Вважаємо, що події А сприяє m випадків, а В – k. Оскільки ми не вважаємо, що А і В несумісні, то існує l випадків, що сприяють А і В разом. Тоді
Р(АВ)=l/n, P(A)=m/n, P(B/A)=l/m,

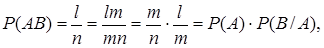
що і треба було довести.
Зауваження. При доведенні теореми не має значення, яку подію вважати першою, а яку другою. Тому ще і
Р(АВ)=Р(B) ×Р(А/В)
Наслідок 1.Якщо подія А не залежить від події В, то подія В не залежить від події А.
Доведення:
Із того, що А не залежить від В, випливає, що Р(А) = Р(A/В). Відомо, що Р(АВ) = Р(А)Р(В/А) або Р(АВ) = Р(В)Р(А/В). Звідси Р(А)Р(В/А)=Р(В)Р(А/В) Þ Р(В)=Р(В/А).
Останнє означає, що В не залежить від А.Отже, події А і В взаємонезалежні.
Таким чином події називаються незалежними, якщо поява однієї із них не змінює ймовірності появи іншої.
Наслідок 2. Ймовірність добутку двох незалежних подій дорівнює добутку ймовірностей цих подій.
Доведення:
Р(АВ)=Р(А)Р(В/А), але Р(В/А)=Р(В), бо події А і В незалежні за умовою. Отже, Р(АВ) = Р(А)Р(В).
Теорема добутку ймовірностей може бути узагальнена на випадок більш ніж двох подій.
Наприклад, Р(АВС) = Р(АВ)Р(С/АВ) = Р(А)Р(В/А)Р(С/АВ). Якщо події А, В, С незалежні, то Р(АВС) = Р(А)Р(В)Р(С).
Приклад. В партії з 10 виробів 6 виробів першого ґатунку, а 4 – другого. Знайти ймовірність того, що три перші закуплені вироби є вироби першого ґатунку.
Розв’язання:
Нехай подія А – всі три вироби першого ґатунку, 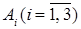 – і-ий виріб першого ґатунку. Тоді А = А1А2А3 Р(А) = Р(А1)Р(А2/А1)Р(А3/А1А2) = (6/10)(5/9)(4/8) = 1/6.
– і-ий виріб першого ґатунку. Тоді А = А1А2А3 Р(А) = Р(А1)Р(А2/А1)Р(А3/А1А2) = (6/10)(5/9)(4/8) = 1/6.
В заключенні відмітемо, що якщо події А і В сумісні, то теорема додавання має вигляд
Р(А + В) = Р(А) + Р(В) – Р(АВ)
Справедливість теореми випливає з малюнка.

Р(А + В + С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС).
Складаємо площі трьох кіл, а потім віднімаємо їх попарно спільні частини, але тоді ділянка, загальна для усіх трьох кіл залишається неврахованою. Для того, щоб не порушувати рівності, в правій частині слід додати ймовірність, що відповідає цій ділянці (pиc. 1).
 |
Формула повної ймовірності
Нехай подія А може відбутися при умові появи однієї з несумісних подій H1, H2, ...,Hn, що утворюють повну групу. Останні події називають… Відомі ймовірності гіпотез і умовні ймовірності P(A/Hі).Треба знайти Р(А)… Маємо:Формула Байеса
Ця формулає наслідком теореми добутку і формули повної ймовірності. Ставиться задача: маємо повну групу несумісних подій H1, H2, ..., Hn… P(AHі) = P(A)P(Hі/A), або P(AHі) = P(Hі)P(A/Hі), звідси маємо, щоПовторення незалежних випробувань
Формула Бернуллі
настане подія А чи ні (настане). Нехай подія А настає у кожному випробуванні з однаковою ймовірністю, а ця… Прикладом незалежних подій може бути перевірка кількох партій виробів на брак, якщо процент браку у кожній з партій…Формула Пуассона
Якщо ймовірність появи події А в кожному з n незалежних дослідів однакова і близька до нуля (0 < p £ 0,1), а кількість дослідів достатньо велика, то ймовірність того, що подія А в n дослідах настане m разів, наближено обчислюється за формулою

де l = np.