ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. РЯДЫ.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра высшей математики и информатики
Л.А. Сараев, Ю.В. Хохрякова,
Е.А. Ильина, В.С. Глущенков
ПРАКТИКУМ ПО МАТЕМАТИКЕ - III
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
РЯДЫ.
Издательство «Самарский университет»
Учебное пособие содержит варианты контрольных заданий и рекомендации к их решению по курсу «Интегральное исчисление. Дифференциальные уравнения. Ряды». Представлены основные методы вычисления неопределенных и определенных интегралов. Рассмотрены способы интегрирования дифференциальных уравнений первого порядка; уравнений высших порядков, допускающих понижение порядка уравнения; изложена методика нахождения частных и общих решений линейных однородных и неоднородных уравнений. Кроме того, детально разобраны основные приемы исследования на сходимость положительных, знакопеременных и функциональных рядов.
Учебное пособие содержит теоретические и практические вопросы для самостоятельной подготовки студентов 2 курса гуманитарных специальностей всех форм обучения.
Авторы-составители: Л.А.Сараев, д.ф.-м.н., профессор, зав. кафедрой высшей математики и информатики СамГУ; Ю.В.Хохрякова, к.ф.-м.н., доцент кафедры высшей математики и информатики СамГУ; Е.А.Ильина, к.ф.-м.н., доцент кафедры высшей математики и информатики СамГУ, В.С.Глущенков, к.ф.-м.н., доцент кафедры высшей математики и информатики СамГУ.
Рецензент: В.П. Радченко, д.ф.-м.н., профессор, зав. кафедрой прикладной математики и информатики СамГТУ.
Содержание
Программа курса «Интегральное исчисление. Дифференциальные уравнения. Ряды.»............................................................................................................................ 4
Тематика контрольных работ................................................................... 6
Методические указания к выполнению расчетного задания 24
Литература................................................. 40
Программа курса.
Интегральное исчисление.
Дифференциальные уравнения. Ряды»
Лекции
Первообразная.
Неопределенный интеграл и его свойства. Примеры.
Методы интегрирования. Использование таблиц интегралов.
Задачи, приводящие к понятию определенного интеграла.
Определенный интеграл, его свойства.
Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов.
Несобственные интегралы с бесконечными пределами, их основные свойства.
Несобственные интегралы от неограниченных функций, их основные свойства.
Дифференциальные уравнения первого порядка.
Задача Коши. Теорема существования и единственности решения задачи Коши.
Уравнения с разделяющимися переменными.
Однородные уравнения.
Линейное уравнение первого порядка.
Уравнение Бернулли.
Уравнения в полных дифференциалах.
Дифференциальные уравнения высших порядков. Задача Коши.
Уравнения, допускающие понижение порядка.
Уравнение Эйлера.
Однородные линейные дифференциальные уравнения. Понятие общего решения.
Неоднородные линейные дифференциальные уравнения.
Метод вариации произвольных постоянных.
Линейные дифференциальные уравнения с постоянными коэффициентами.
Уравнения с правой частью специального вида.
Нормальная система дифференциальных уравнений.
Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
Понятие о числовом ряде, члены ряда, частичные суммы. Положительные ряды, необходимый признак сходимости ряда.
Признаки сходимости, основанные на сравнении положительных рядов.
Достаточные признаки сходимости положительных рядов (признак Даламбера, радикальный признак Коши).
Интегральный признак Коши.
Знакопеременные ряды, теорема Лейбница.
Знакочередующиеся ряды, абсолютная и условная сходимость.
Функциональные ряды, точка сходимости, область сходимости, равномерная сходимость.
Степенные ряды. Теорема Абеля. Радиус сходимости.
Ряды Тейлора и Маклорена. Разложение элементарных функций в ряды Тейлора и Маклорена.
Практические занятия
Замена переменной интегрирования. Методы интегрирования по частям. Определенный интеграл. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов.Тематика контрольных работ
Задача 1
Задача 2
1. 12. 2. 13. 3. 14. 4. … 23. 27. 24. …Задача 3
Вычислить определенные интегралы. 1. 6. 2. …Задача 4
1. 16. 2. 17. 3. 18. 4. …Задача 5.
1. 16. 2. 17. 3. 18. 4. …Задача 6
1. 2. 3. 4. 5. 6. …Задача 7
1. 16. 2. 17. 3. 18. 4. …Задача 8
1. 16. 2. 17. 3. 18. 4. …Задача 9
1. 2. 3. 4. 5. 6. …Задача 10
1. 16. 2. 17. 3. 18. 4. …Задача 11
1. в окрестности точки 2. в окрестности точки 3. в окрестности точки 4. …Методические указания к выполнению расчетного задания
Задача 1
Данный метод основан на использовании формулы интегрирования по частям. Формула интегрирования по частям имеет видРешение.
Пусть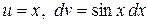 
, тогда 
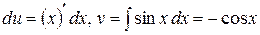. По формуле интегрирования по частям получаем
.
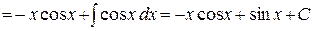Задача 2
Формула замены переменной в неопределенном интеграле имеет видЗадача 3
Для вычисления определенного интеграла используют формулу Ньютона–Лейбница .Задача 4
Задача 5.
Уравнение вида , где и известные функции от , линейное (первой степени)… Посредством замены функции произведением двух вспомогательных функций линейное уравнение сводится к двум уравнениям с…Задача 6
. Если в уравнении 1-го порядка коэффициенты и удовлетворяют условию , то его левая часть есть полный дифференциал…Задача 7
. 1) Уравнение -го порядка решается последовательным интегрированием. Умножая обе его части на и интегрируя, получаем уравнение -го порядка:Задача 8
.Задача 9
Числовым рядом называется выражение , (1) где числа , , … , , … , называемые членами ряда, образуют известную числовую последовательность.Задача 10
Ряд , члены которого являются функциями от переменной , называется функциональным. При различных значениях из функционального ряда получаются различные числовые… Совокупность значений , при которых функциональный ряд сходится, называется его областью сходимости.Задача 11
Рядом Тейлора для функции в окрестности точки называется степенной ряд… .Литература
1. Гусак А.А. Высшая математика. – Минск, 1998. – Т.1-2.
2. Кремер П.Ш. Высшая математика для экономистов. – М., 1999.
3. Щипачев В.С. Высшая математика. – М., 1998.
4. Красс М.С. Математика для экономических специальностей. – М., 1999.
5. Бугров Я.С., Никольский С.М. Высшая математика. – Т.1-2.
6. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. – М. – Т.1-2.
[1] В частности, если , то – многочлен; а если есть постоянная (многочлен нулевой степени), то – показательная функция .
[2] Нижним пределом интеграла может быть любое положительное число из области определения .