МАТЕМАТИЧЕСКИЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ

Квантовая механика микрочастицы, не ограниченная полуклассическим приближением, строится на математическом основании, использующем гильбертого пространство функций, то есть множество функций, для которых определено скалярное произведение в интегральной форме.

Основные положения

Состояние частицы описывается волновой функцией. Множество возможных состояний образует гильбертого пространство. Волновая функция получается в результате решения уравнения Шредингера. Физическая величина описывается оператором, действующим в гильбертовом пространстве.

ВОЛНОВАЯ функция

Состояние частицы описывает комплексная волновая функция Y (пси), являющаяся амплитудой вероятности обнаружения частицы: .

ОператорЫ

Физическая величина A (координата, импульс, энергия и другие) описывается линейным оператором . Исключением является время, которое считается параметром. Подразумевается, что правее оператора находится функция, на которую он действует.

Рассмотрим явный вид операторов координаты и импульса в координатном представлении. Обоснование вида будет дано далее.

Оператор координаты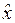

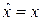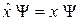, . (2.1)

Действие оператора координаты сводится к умножению функции на координату.

Оператор проекции импульса

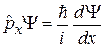, . (2.2)

Действие оператора импульса сводится к дифференцированию функции по координате и умножению на .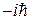

Свойства линейных операторов:

1) Умножение на число с

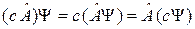. (2.3)

Число можно вынести из под знака действия оператора.

2) Линейность

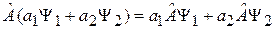, (2.4)

где 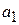и 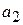– числа. Действие оператора на сумму функций равно сумме действий оператора на каждую функцию.

3) Сложение (вычитание) операторов

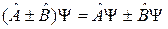. (2.5)

Действие суммы операторов на функцию равно сумме действий каждого оператора на функцию.

4) Умножение оператора на оператор

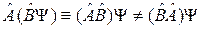. (2.6)

Вначале действует ближайший к функции оператор, затем на полученную функцию действует оператор, находящийся левее. Перемножаемые операторы в общем случае не перестановочны, например:

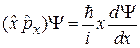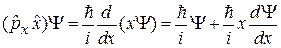Перестановочное соотношение, или коммутатор операторов

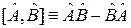Операторы и коммутируют, если .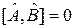

Примеры:

, ,

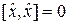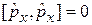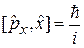. (2.7)

Собственные функции операторА

И собственные значения

Собственная функция оператора определяется уравнением , (2.8)

ЭрмитовыЙ оператор

Для обеспечения вещественности и однозначности результатов измерения физической величины ее оператор должен быть эрмитовым. Операция эрмитового сопряжения определяется через интегральную квадратичную форму. Такая форма описывает, в частности, среднее значение измеряемой величины.

Эрмитово сопряженный оператор 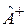обозначается значком «+» и определяется в виде

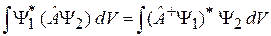. (2.11)

Интегрирование проводится по всему объему пространства, занятого частицей.

Свойства эрмитового сопряжения

, ,

ЭРМИТОВОСТЬ ОПЕРАТОРА ИМПУЛЬСА

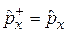Доказательство:

Левая сторона (2.14)

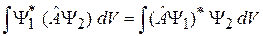
с оператором 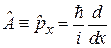имеет вид

Вычисляем правую сторону (2.14)

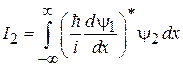
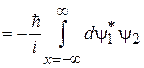В результате

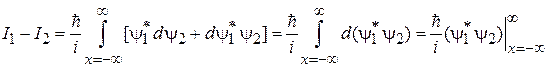Волновые функции квадратично интегрируемы и равны нулю на бесконечности, поэтому 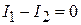, и оператор импульса эрмитов.

УсЛОВИЯ ОРТОНОРМИРОВАННОСТИ

Собственные функции любого эрмитового оператора образуют ортонормированный базис . Спектр базиса зависит от и может быть дискретным или непрерывным.… Дискретный спектр n. Выполняется нормировка , тогда условие…

СРЕДНЕЕ ЗНАЧЕНИЕ ВЕЛИЧИНЫ

Собственные функции эрмитового оператора образуют ортонормированный базис . Если частица находится в состоянии Ψ, являющемся суперпозицией… Разложение состояния Ψ по базису имеет вид: для дискретного спектра

СоотношениЕ неопределенностей

Для измерения величины a, описываемой оператором , частица в исследуемом состоянии приводится во взаимодействие с соответствующим прибором. Его… ,

ОператорЫ трансляции И ЭВОЛЮЦИИ

Развитие состояния частицы во времени описывает волновое уравнение Шредингера. Для вывода уравнения используем оператор эволюции, сдвигающий состояние объекта во времени. Он строится по аналогии с оператором трансляции, перемещающим состояние в пространстве.

Оператор трансляции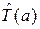сдвигает состояние объекта на расстояние а

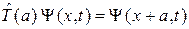. (2.44)

Для получения оператора 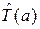разлагаем 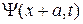в ряд Тейлора

Производную по координате выражаем через оператор импульса 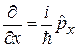, находим

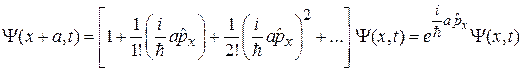где квадратная скобка является разложение в ряд экспоненты. В результате оператор трансляции

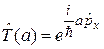. (2.45)

Генератор трансляции пропорционален быстроте изменения оператора трансляции по параметру смещения вблизи нуля

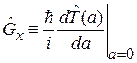. (2.46)

Определению (2.46) удовлетворяет

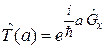Сравнение с (2.45) дает

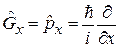. (2.47)

Генератором перемещения является импульс.

Оператор эволюции 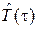передвигает состояние во времени на τ

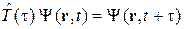. (2.49)

По аналогии с (2.45) записываем

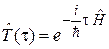. (2.50)

Знак минус в (2.50) обусловлен разными знаками пространственного и временного слагаемых в фазе волны де Бройля (1.11)

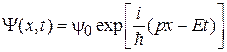Генератор эволюции

сравниваем с генератором трансляции (2.46) и по аналогии с (2.47) получаем ,

Уравнение Шредингера

Для частицы, описываемой гамильтонианом , волновая функция находится из уравнения, которое получил Эрвин Шрёдингер в 1926 г. Если потенциальная… Правило соответствия. При переходе от классической к квантовой теории… Оператор Гамильтона. Гамильтониан частицы в классической теории является суммой кинетической и потенциальной энергий,…