Тепловое излучение

Лекция 1.

Тепловое излучение

Тепловое излучение – это испускание электромагнитных волн за счёт внутренней энергии тел. Тепловое излучение имеет место при любой температуре. При… Излучение будет равновесным, если распределение энергии между телом и… Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла…

Эффект Комптона

Комптон исследовал рассеяние жесткого рентгеновского из­лучения на образцах, состоящих из легких атомов, таких как графит, парафин и др. Схема его… Источником рентгеновского излучения служила рентгенов­ская трубка с… Комптон обнаружил, что в рассе­янном излучении, наряду с исходной длиной волны λ, появля­ется смещенная линия с…

Тормозное рентгеновское излучение

= . (1.19) Эту формулу можно интерпретировать и иначе: не как переход энергии светового… eU=.

Корпускулярно-волновой дуализм света

Эффект Комптона и фотоэффект подтверждает корпускулярную природу света. Свет ведет себя как поток частиц – фотонов. Тогда как же частица может… Противопоставление квантовых и волновых свойств света друг другу является… Взаимосвязь корпускулярно-волновых свойств света объясняется статистическим подходом к исследованию распространения…

Лекция 4

Двойственная корпускулярно-волновая природа

Частиц вещества

Гипотеза де Бройля

а частота ω = Е/ħ, т.е. корпускулярно-волновой дуализм присущ всем… Если частица имеет кинетическую энергию Е, то ей соответствует длина волны де Бройля:

Свойства волн де Бройля

Рассмотрим движение свободного электрона. По де Бройлю, ему соответствует длина волны: . Будем называть ее электронной волной. Известно, что λ = фаз/, где фаз – фазовая скорость распространения волны.…

Лекция 5

3.1.Волновая функция Всякая микрочастица – это образование особого рода, сочетающее в себе свойства… Отличие микрочастицы в квантовой механике от обычной микрочастицы заключается в том, что она не обладает одновременно…

Принцип неопределенности

(3.1)   – чем меньше неопределенность координаты Δх, тем больше неопределенность импульса Δрх, и наоборот.

Уравнение Шредингера

Вероятностное (статистическое) истолкование волн де Бройля и соотношение неопределенностей указывают, что уравнение движения в квантовой механике… Уравнение Шредингера имеет следующий вид: . (3.3)

Ядерная модель атома

Если все это так, то атом должен быть в высокой степени прозрачным для пронизывающих его частиц. Экспериментальное доказательство изложенной модели… Было обнаружено, что подавляющее число α- частиц рассеивалось на… Исходя из предположений, что взаимодействие указанных α-частиц с ядром является кулоновским, а заряд и масса ядра…

Постулаты Бора. Опыты Франка и Герца

Атом может длительное время находиться только в определенных, так называемых стационарных состояниях, которые характеризуются дискретными значениями… При переходе атома из стационарного состояния с большей энергией E2 в… ħω =E2-E1. (4.11)

Боровская модель атома водорода

M=nħ, n=1,2,3,…, (4.12) где n — квантовое число. С помощью этого правила квантования можно найти радиусы круговых стационарных орбит водородоподобных систем (Н, Не+,…

Согласно 2-му закону Ньютона

где m —масса электрона. Отсюда кинетическая энергия электрона (4.14) и полная энергия электрона в кулоновском поле ядра

Тогда постоянная Ридберга

Как видим, постоянная Ридберга зависит и от массы ядра. Для атома водорода, ядром которого является протон, формула (4.19) дает значение, более… Приведенная на рис.4. 6 система энергетических уровней помогает наглядно… Систему энергетических уровней атома принято называть и иначе — системой термов. Терм Т — это величина, определяе­мая…

Операторы физических частиц

 

6.1 Линейные операторы. Собственные функции и

собственные значения операторов

 

Оператор есть символ для обозначения действия или программы действий, которые нужно совершить над некоторой функцией, чтобы получить другую функцию.

Операторы обозначаются большими латинскими буквами со «шляпкой» наверху: Â, 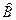. Если оператор стоит рядом с функцией и слева от нее, то это означает, что он действует на функцию. В результате получается новая функция тех же переменных:

 

ÂΨ = ψ.

 

Функции Ψ и ψ должны относиться к одному классу функций. Невозможен, например, переход от функции действительного переменного к функции комплексного.

Примеры операторов:

1) Â = х– оператор умножения на переменную х;

2) 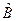= ∂/∂х - оператор дифференцирования по х;

3) 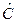= перейти к комплексно-сопряженному выражению.

Результаты действий этих операторов:

1) Â ψ = хψ; 2) 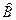ψ = ∂ψ/∂х; 3) Ĉψ = ψ*.

Оператор называется линейным, если для него выполняется условие:

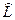(c₁ψ₁ + c₂ψ₂) = c₁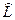ψ₁ + c₂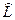ψ₂,

где ψ₁ и ψ₂ – функции, с₁, с₂ – постоянные (комплексные числа).

Например, операторы дифференцирования и умножения на переменную величину линейны, а возведения в степень – нет.

Символы операторов рассматриваются как самостоятельные математические объекты, над которыми можно производить ряд математическими действий: сложения, умножения, возведения в степень, разложение в степенной ряд:

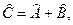если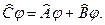

Сложение ассоциативно и коммутативно:

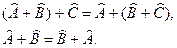
Оператор Ĉ называется произведением операторов:

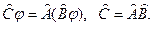
Операторы, для которых 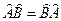, называется коммутирующими. Оператор 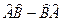называется коммутатором операторов Â и 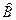, и обозначается .

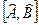Для коммутирующих операторов [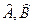] = 0.

Равенство называется уравнением для собственных значений и собственных функций оператора Â, здесь ψ – функция, а – число.

Если функция удовлетворяет стандартным требованиям для ψ – функции, то она называется собственной функцией оператора Â, принадлежащей его собственному значению а. Совокупность всех собственных значений называется спектром оператора. Спектр бывает дискретным, непрерывным или смешанным.

Собственное значение называется вырожденным, если ему соответствует несколько линейно независимых собственных функций. Число таких функций называется кратностью вырождения.

Оператор Â называется самосопряженным или эрмитовым, если выполняется равенство:

.

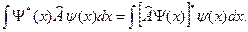Например, Â = х; 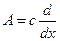- самосопряженные операторы.

Сумма самосопряженных операторов есть самосопряженный оператор. Применение самосопряженных операторов в квантовой механике обуславливается тем, что их собственные значения всегда вещественны. Собственные функции эрмитовых операторов попарно ортогональны.

Для эрмитовых операторов характерна полнота системы собственных функций. Это значит, что в случае дискретного спектра по собственным функциям эрмитового оператора может быть разложена любая функция состояния в обобщенный ряд Фурье. В случае непрерывного спектра разложение производится в интеграл Фурье.

6.2 Операторы и допустимые значения физических величин. Оператор Гамильтона. Вычисление средних значений физических величин

Итак, энергия микросистем, как мы видели на примере частицы в потенциальной яме и гармоническом осцилляторе, принимает дискретные значения, квантуется. Это значит, что использовать для энергии и других величин просто вещественные числа или векторы, как это делалось в классических электродинамике и механике, нельзя: не все точки числовой оси для энергии допустимы. Связь между физической величиной и ее математической моделью устанавливается постулатом: в квантовой механике основным физическим величинам сопоставляются линейные самосопряженные операторы. Обычно, оператор обозначается той же буквой, что и величина в классической физике.

Исходными являются операторы координат и импульса. Оператор координаты х есть действие умножения на эту переменную:

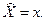
Оператор проекции импульса: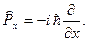

Операторы других величин можно найти, учитывая, что соотношения между операторами физических величин такие же, как и между этими величинами в классической физике:

оператор радиус – вектора

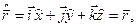
импульса

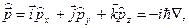
момента импульса

,

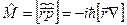кинетической энергии

,

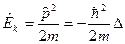потенциальной энергии

,

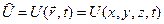полной механической энергии

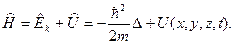
Оператор полной энергии называется оператором Гамильтона или гамильтонианом. Он играет особую роль, ибо его собственные функции оказывается волновыми функциями стационарных состояний. Кроме того, он входит в уравнение Шредингера.

Связь между оператором и наблюдаемыми при измерениях значениями физической величины дается постулатом: физическая величина может приниматься те и только те значения, которые совпадают с собственными значениями ее оператора.

Наиболее полное описание квантовой системы достигается заданием соответствующей этому состоянию волновой функции. В ней заключена вся информация о системе. Функция состояния позволяет определить плотность вероятности для положения частицы в пространстве и ее изменения во времени. С помощью волновой функции осуществляется расчет возможных результатов физических экспериментов и измерений физических величин, определяются средние значения физических величин в заданном состоянии. Изменение волновой функции во времени отражает изменение состояния квантовой системы под действием внешних сил.

Для определения функции состояния в каждом конкретном случае микросистемы записывается уравнением Шредингера:

.

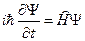В такой записи уравнение Шредингера пригодно для любых квантовых объектов. В зависимости от вида микрочастицы (отдельная частица, атом, кристалл) изменяется вид оператора Гамильтона, структура же уравнения остается неизменной.

Оператор Гамильтона характеризует микросистему с динамической стороны, его вид зависит от масс частиц, их электрических зарядов, взаимодействия между ними. В принципе гамильтониан должен быть задан в конкретных задачах квантовой механики подобно тому, как задаются силы в классической механике при использовании второго закона Ньютона.

Волновые функции – решения уравнения Шредингера – являются комплексными функциями вещественных переменных. Аргументы волновой функции – координаты и время.

Состояние квантовой системы описывается волновой функцией, которая ничего не говорит о значениях физических величин, которыми характеризуются система. Такую информацию дает только измерение, результат которого не всегда однозначен. Получение того или иного значения на опыте в ряде случаев является случайным событием. Тогда говорят, что величина не имеет определенного значения. Однако можно рассчитать вероятность данного значения при многократных измерениях, располагая функцией состояния: вероятность того, что при измерении получится значение а_i физической величины А, равна квадрату модуля соответствующего коэффициента Фурье в разложении волновой функции в ряд или интеграл Фурье по собственным функциям оператора этой физической величины.

Пусть Ψ – волновая функция частицы, чтобы рассчитать искомые вероятности, представим ее в виде ряда:

,

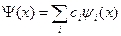где ψ_i – собственные функции оператора Â, имеющего дискретный спектр, тогда вероятность получения а_i есть:

.

В случае непрерывного спектра волновая функция разлагается в интеграл Фурье. Если ψ(а,х) – собственная функция, то:

.

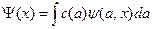Поскольку теперь мы имеем непрерывное множество значений величины А, то в строгом смысле слова нельзя говорить о вероятностях отдельных значений. Вероятность dΩ попадания значений величины в интервал от а до (а + da) равна:

dΩ(a) = ω(a)da,

где ω(а) – плотность вероятности (функция распределения вероятностей) равна квадрату модуля коэффициента с(а):

.

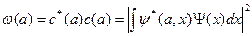Ясно, что определенного значения у величины нет, если функция состояния не является собственной для оператора этой величины. В этом случае определяют среднее значение достаточно большого числа измерений:

.

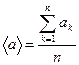Для теоретической оценки среднего значения физической величины достаточно знать функцию состояния частицы (предполагается, что вид оператора этой величины известен). Если а_i – собственные значения оператора Â и Ω_i – вероятности их обнаружения, то среднее значение:

.

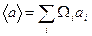Подставив Ω_i, имеем:

,

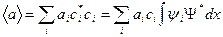где Ψ – волновая функция, ψ_i – собственные функции оператора Â(Âψ_i = а_iψ_i), тогда:

 

.

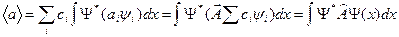Вычисление средних имеет большое значение для микромира. Когда в рассматриваемом состоянии физическая величина не имеет определенного значения, среднее значение характеризует состояние.

Понятно, что если Ψ = ψ_i, то:

,

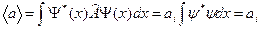где ψ^* = 1.

В стационарном состоянии: .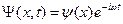

Если оператор физической величины не содержит времени, то его собственные функции и собственные значения также не зависят от времени. Поэтому в стационарных состояниях распределение вероятностей для значений рассматриваемой величины также оказывается стационарным, независящим от времени. Постоянно и среднее значение.

Условием существования определенных значений двух физических величин в одном и том же состоянии системы является коммутация их операторов.

Например, операторы импульса и кинетической энергии коммутируют:

,

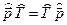поэтому кинетическая энергия и импульс микрочастицы имеют определенные значения.

Для координаты и импульса коммутатор равен

,

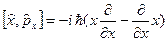и 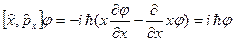, тогда 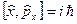- коммутатор отличен от нуля, операторы 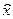и 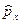не коммутируют. Значит, не существует состояний, в которых были бы вместе точно заданы координата х и проекция импульса р_х.

6.3. Законы сохранения физических величин в

квантовой механике

В классической механике выполняются законы сохранения энергии, импульса и момента импульса – величин, имеющих универсальное применение во всей физике. В микромире к ним добавляется закон сохранения четности – величины, специфической для квантовой физики.

Рассмотрим условие сохранения определенного значения физической величины. Если функция состояния Ψ, в котором находится система, совпадает с собственной функцией ψ_i оператора Â, то величина имеет определенное значение а_i. Если производная по времени от оператора Â равна нулю (оператор не зависит от времени), то определенное значение а_i сохраняется.

Закон сохранения энергии. В стационарных полях оператор Гамильтона не зависит от времени, 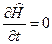, поэтому энергия <Е> = const. Если функция состояния системы в стационарном поле собственная для оператора Гамильтона, то энергия имеет определенное сохраняющееся значение. Такое состояние является стационарным. Энергия микрочастицы в стационарном поле сохраняется.

Закон сохранения импульса. Оператор импульса частицы не содержит времени и коммутирует с оператором Гамильтона для свободной частицы 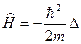. Следовательно, импульс свободной частицы сохраняется.

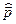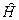Если частица находится в силовом поле, то оператор Гамильтона содержит координаты, на которые действует оператор импульса, т.е. и не коммутируют. В силовом поле импульс не сохраняется.

Для замкнутой системы микрочастиц импульс сохраняется.

Закон сохранения момента импульса. Оператор момента импульса частицы 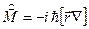не содержит времени и коммутирует с оператором Гамильтона свободной частицы, следовательно, момент импульса свободной частицы сохраняется.

В общем случае в силовом поле момент импульса не сохраняется. В замкнутой системе микрочастиц момент импульса сохраняется.

Четность, закон сохранения четности

, или х´ = - х; у´ = - у; z´ = - z.

СТАЦИОНАРНЫЕ ЗАДАЧИ КВАНТОВОЙ МЕХАНИКИ

Частица в потенциальном ящике с бесконечно высокими стенками

Рассмотрим частицу, находящуюся в бесконечно глубокой одномерной потенциальной яме. Будем считать, что частица может двигаться только в направлении… в ящике равна нулю, а за пределами ящика . Уравнение Шредингера Шредингера для такой частицы имеет вид:

Движение частицы в потенциальном ящике конечной глубины

Примером такой ситуации является движение коллективизированных электронов внутри металла (согласно классической электронной теории вне металла… Применим к частице в таком потенциальном ящике уравнение Шредингера (будем… В области I .

Прохождение частицы через потенциальный барьер

Если же Е меньше , то частица отражается от барьера и летит обратно, сквозь барьер она проникнуть не может. Согласно же квантовой теории даже при имеется отличная от нуля вероятность… Рассмотрим частицу, подлетающую к барьеру с энергией . Уравнение Шредингера для такой частицы имеет вид:

Лекция 9-10

Атом водорода и водородоподобные системы

Свойства оператора момента импульса и его проекций. Собственные значения и собственные функции оператора момента импульса и его проекций

Оператор момента импульса имеет вид: 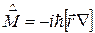. Оператор проекций момента импульса:

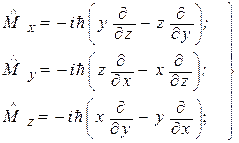(7.1)

Эти операторы не коммутируют друг с другом, поэтому не существует состояний с тремя определёнными проекциями момента импульса (за исключением ).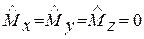

Оператор квадрата момента импульса 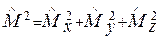коммутирует с операторами проекций 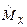, , 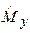.Это означает, что возможны состояния с определённым модулем момента импульса (с определённым значением М²) и какой-нибудь из его проекций. При изучении движения частиц в центральном поле целесообразно использовать сферические координаты r, θ, φ, причём

x = r ·sin θ ·cos φ; y = r ·sin θ ·sin φ; z = r ·cos θ;

Тогда

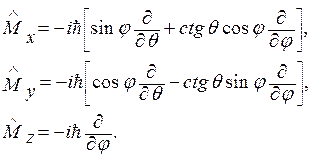
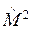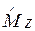Поскольку ось ОZ выбрана в качестве полярной оси, равноправие трёх декартовых осей координат ОX, OY, OZ при переходе к сферическим координатам теряется: теперь некоторое направление в пространстве выделено, и удобно рассматривать состояние с определёнными значениями и . Коммутирующие операторы 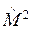и 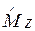имеют общую систему собственных функций. Для того, чтобы найти эти функции, нужно решить уравнение:

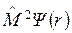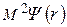= (7.2)

В сферических координатах: 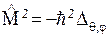, (7.3)

где 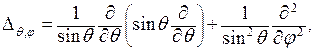поэтому уравнение (7.2) принимает вид:

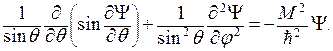
Оно имеет однозначные, непрерывные и всюду ограниченные решения при условии: 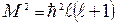, (где 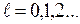), которые определяются собственными значениями оператора квадрата момента импульса. Таким образом, значения квадрата модуля момента импульса частицы квантуются. Квантовое число 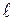определяет модуль момента импульса. Состояния с небольшими значениями 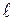часто обозначаются буквами:

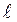
обозн.	s	p	d	f	g	h	i

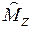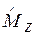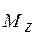Состояния с заданным моментом импульса вырождены по квантовому числу m. Физический смысл этого квантового числа раскрывается при решении задачи о собственных функциях и собственных значениях оператора проекции момента импульса . Уравнение Ψ = Ψ или 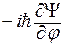= 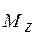Ψ имеет частные решения вида:

Ψ = 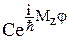. Поскольку полный обход вокруг оси ОZ при изменении угла φ на 2π приводит нас в исходную точку пространства ( r и θ постоянны ), то из условия однозначности решения следует равенство: 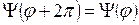. Оно удовлетворяется, если положить 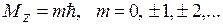. После нормировки и подстановки 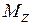собственные функции оператора 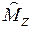принимают вид: .

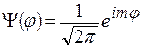Часто используют название: 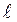- азимутальное или орбитальное квантовое число, причём 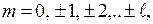т.е. принимает 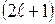значение.

В целях наглядности результаты квантования момента импульса и его проекции можно представить графически. Из точки 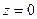построим полуокружность, радиус которой равен модулю момента импульса. На рис. 7.1. 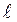=2 . Радиус окружности равен 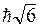. По аналогии с классикой принято сопоставлять состоянием с одним 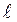и разными m различные определённые ориентации вектора момента импульса, хотя две другие проекции и не имеют определённого значения. Очень важное различие квантового и классического моментов импульса заключаются в том, что отношение 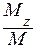(косинус угла наклона) в квантовом случае принимает дискретный ряд значений. Этот факт получил название пространственного квантования.

Рис.7.1.

Движение частицы в центрально -симметричном

Поле

Центрально-симметричным называется силовое поле с потенциальной энергией, зависящей только от расстояния до некоторого центра. Центр удобно взять в качестве начала координат, тогда U = U(r).

Сила, действующая на частицу в таком поле, направлена по полярному радиусу, проведенному в данную точку. Поэтому при движении классической частицы сохраняется полная механическая энергия и момент импульса. Следует ожидать этого и в квантовой механике.

Уравнение Шредингера запишем в сферических координатах:

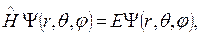
Где

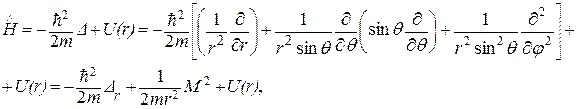(7.4)

.

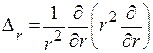Если сравнить формулы (7.1), (7.2), (7.3) то видно, что операторы 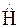, 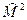и 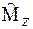коммутируют друг с другом. Таким образом, существуют стационарные состояния, в которых одновременно задана энергия, момент импульса и его проекция на некоторую ось, принятую за ось ОZ.

Уравнения (7.4) допускает разделение переменных. Волновую функцию представим в виде произведения радиального R(r) и углового 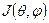множителей:

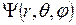= R(r) ,

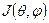после подстановки получаем уравнение:

.

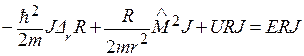Умножим его на 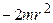и разделим на RJ:

.

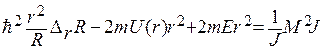Правая и левая части этого равенства есть функции разных независимых переменных, поэтому они должны быть равны одной и той же постоянной величине. Обозначим её через λ, тогда исходное уравнение распадается на два:

,

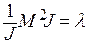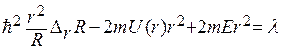
Первое из них есть уравнение для собственных функций и собственных значений оператора квадрата момента импульса. Его решение нам известно, причём 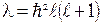, тогда второе уравнение принимает вид:

.

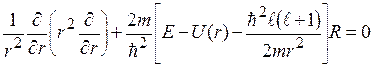Это уравнение называется радиальным. Сделаем подстановку 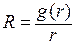, тогда 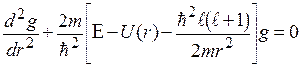. (7.5)

Уравнение (7.5) по форме совпадает с одномерным уравнением Шредингера для движения частицы в поле эффективным потенциалом: Uэф 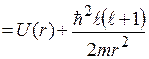. Дальнейшее решение требует знания вида потенциала U(r).

Таким образом, при движении частицы в центрально-симметричном поле:

Возможны стационарные состояния с определенными значениями энергии, момента импульса и его проекций на ось OZ.

2) Указанные состояния различаются квантовыми числами 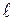и m, определяющими момент импульса и его проекцию.

Энергия стационарного состояния зависит от конкретного вида центрального поля и должна быть определена вместе с радиальным множителем R(r) в процессе решения уравнения (4).

Квантово -механическая модель атома водорода

, где . Поле является центрально-симметричным, поэтому воспользуемся результатами… ,

Для нас наиболее важна область потенциальной ямы. Здесь при отрицательных энергиях движение частицы происходит в ограниченной области пространства и возможны связанные состояния с дискретными значениями энергии.

Запишем радиальное уравнение с кулоновским потенциалом:

.

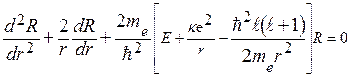Для упрощения перейдём к безразмерной величине 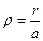, 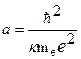- постоянная, называемая боровским радиусом (a = 0,52∙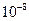см). Эта величина определяет порядок расстояний в атоме. Обозначим:

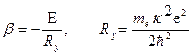(7.6)

Постоянная 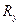имеет размерность энергии (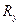=13,6 эВ) и даёт порядок энергии электрона в атоме. Тогда радиальное уравнение принимает вид:

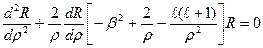. (7.7)

Это уравнение необходимо решить для нахождения неполной радиальной функции R(r).

(7.8) где = 1,2,3,… - радиальное квантовое число. Обычно вводят главное квантовое число: (7.9)

Орбитальный магнитный момент электрона

Из этих формул видно, что существует своеобразный квант магнитного момента − наименьшее отличное от нуля значение проекции момента на…

Спин электрона

Иногда электрон представляют для наглядности в виде шарика-волчка, вращающегося вокруг оси, проходящей через центр масс. С принципиальной стороны… Для описания спина используется оператор спина и операторы , , его проекций.… (7.10)

Линейчатые спектры атомов с одним

Валентным электроном

Если n (главное квантовое число) велико, то электрон движется далеко от атомного остатка и находится в центральном поле одного заряда (равного… Если же электрон подходит близко к атомному остатку, то он своим полем… Спектральные термы щелочных атомов выражаются формулой:

Ширина спектральных линий

Основное же состояние атома стационарно, из него невозможен спонтанный переход…

Мультиплетность спектров

Исследования спектров щелочных металлов показали, что каждая линия этих спектров является двойной (дуплет). Структура спектра, отражающая… Число компонент в мультиплете может быть два (дуплет), три (триплет), четыре и… Расщепление спектральных линий обусловлено расщеплением энергетических уровней и связано с наличием у электрона…

Полный механический момент

Многоэлектронного атома

1. Моменты взаимодействуют между собой сильнее, чем с , которые в свою очередь сильнее связаны друг с другом, чем с . Вследствие этого моменты… 2. Каждая пара и взаимодействует между собой сильнее, чем с другими и ,… Рассмотрим связь Рессель - Саундерса. Орбитальные квантовые числа i всегда бывают целыми. Тогда квантовое число L…

Магнитный момент атома

где – магнетон Бора. Минус в формуле означает, что магнитный и механический…

Векторная модель атома

Пусть и Мz имеют определенные значения (Мх и Му при этом не определены, т.к. неопределено направление в пространстве). В таком случае вектор может… Допустим, что в направлении z создано магнитное поле . С механическим моментом…  

Механика системы микрочастиц

Волновая функция системы микрочастиц

Ψ = Ψ(х1, х2,…, хN , t), где хi совокупность трех координат точки пространства, в которой может… Вероятность того, что частица находится в элементе объема около точки с координатами х1, у1, z1 и одновременно с этим…

Тождественность частиц одного и того же вида и

Принцип Паули

Квантовая система, состоящая из одинаковых частиц, например, электронов, протонов, фотонов и т.д., обладает некоторыми новыми свойствами, не… В микромире имеют место дискретные значения величин, характеризующих… Принцип тождественности связан и с тем, что при тесном сближении невозможно проследить за каждой частицей в…

Лекция 14

В 1869 г. Менделеев открыл периодический закон изменения химиче­ских и физических свойств элементов в зависимости от их атомных масс. Химические… Порядковый номер элемента z в периодической системе совпадает с числом… Теория периодической системы основывается на следующих компо­нентах:

Многоэлектронные атомы

z = 1 – атом водорода. Один электрон находится в состоянии с п = 1, энергия электрона равна – 13,6 эВ. Энергия связи равна энергии ионизации 13,6… z = 2 — гелий. Ион гелия Не+ - водородоподобный ион. Любое ядро с атомным… .

Эффекты Зеемана и Штарка

Спектральная линия с частотой расщепляется на две или три компо­ненты. Если излучение распространяется перпендикулярно к направлению напряженности… Если излучение распространяется вдоль направления магнитного поля, то линия… .

Рентгеновские спектры

Тормозное излучение получается при не слишком больших энергиях бомбардирующих атом электронов. Это излучение обладает сплошным спектром и не зависит… Рентгеновские спектры состоят из нескольких серий: К, L, М, N и О. Каждая… Если вырывается один из электронов К-слоя, то освободившееся место может быть занято электроном из какого-либо…

Двухатомная молекула

Ионная и ковалентная связь. Молекула водорода. Обменный интеграл

Второй вид связи наблюдается в тех молекулах, в которых часть элек­тронов движется около обоих ядер. Такая связь называется гомеополярной (или… Простейшей молекулой с гомеополярной связью является молекула во­дорода.… Потенциальная энергия такой системы равна:

Молекулярные спектры

Для электронно-колебательных полос характерно наличие резкого края, называемого кантом полосы. Другой край такой полосы оказывается размытым. Кант… Энергия двухатомной молекулы складывается из электронной, колеба­тельной и… Т.к. , то при слабых возмущениях изменяются только , при более сильных , и лишь при еще более сильных возбуждениях…

Лекция 16

Генераторы когерентного света

Возможность существования процессов вынужденного излучения, являющихся основой лазерной техники, была предсказана в 1916.г Эйнштейном. Он… Первое экспериментальное подтверждение возможности усиления света было… В квантовой электронике мы имеем дело не с одним атомом (молекулой), а с большим их числом, т.е. с некоторым ансамблем…

На рис. 11.1 представлена диаграмма энергетических уровней, причем длина горизонтальной черты определяет населенность того или иного энергетического уровня.

Свет представляет собой электромагнитные волны, энергия электромагнитного поля также квантована, каждый квант излучения (фотон) имеет энергию .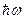

 

Атом может взаимодействовать с электромагнитным излучением, изменяя при этом свое энергетическое состояние, т.е. совершать переход с одного уровня на другой. При поглощении электромагнитной энергии происходит переход атома в состояние с большей энергией (на более высокий уровень). При переходе на нижний уровень атом излучает фотон.

Если атом находится в верхнем энергетическом состоянии с энергией E_m, то имеется определенная вероятность того, что через некоторое время он перейдет в нижнее состояние E_n, при этом излучается фотон:

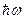_{m n} = E_m – E_n.

Вероятность перехода атома с одного энергетического уровня на другой имеет две составляющие. Первая зависит от свойств атома и не зависит от внешних факторов. Вторая – линейно зависит от плотности энергии поля, соответствующей частоте перехода, действующего на атом извне. Первая определяет спонтанное излучение, вторая – вынужденное, индуцированное. При воздействии света частотой 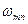на атом, находящийся на нижнем энергетическом уровне п, происходит поглощение фотона с энергией , сопровождаемое переходом атома на верхний уровень m. Спонтанного перехода атома с нижнего уровня на верхний не происходит.

Коэффициент спонтанного перехода A_mn определяет вероятность спонтанного перехода изолированного атома в единицу времени с уровня m на уровень n. Коэффициенты вынужденного излучения B_mn и поглощения B_nm определяют вероятность соответствующих переходов в единицу времени при воздействии на атом электромагнитной энергии со спектральной плотностью, равной единице. Эйнштейн установил соотношения для коэффициентов излучения и поглощения молекул, находящихся в тепловом равновесии:

r_wB_nmN_n = r_wB_mnN_m + A_mnN_n, (11.3)

где r_w – плотность энергии излучения на соответствующей частоте перехода между уровнями m и n, B_nmN_n – вероятность вынужденных переходов в единицу времени с уровня n на уровень m под влиянием излучения с плотностью энергии r_w, т.е. вероятность поглощения; B_mnN_m – вероятность вынужденных переходов с уровня m на n, т.е. вероятность вынужденного излучения. Левая часть уравнения (11.3) определяет поглощенную в единицу времени энергию, а правая – полную энергию излучения при вынужденных и спонтанных переходах. Из выражений (11.2) и (11.3) получаем:

.

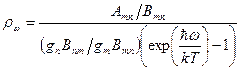Можно показать, что

g_nB_nm = g_m B_mn, ,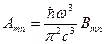

где g_n и g_m-степени вырождения энергетических уровне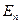й и 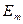. Если энергетические уровни частицы невырождены, то B_nm = B_mn - коэффициенты вынужденного излучения с уровня m на n и поглощения равны.

Принцип действия лазеров

. Общее число переходов атомов с уровня m на уровень n, как спонтанных, так и… .

Схемы накачки

. Действительно, при термодинамическом равновесии уровень n заселен больше, чем… Однако такой механизм работать не будет. Когда наступят условия, при которых населенности уровней окажутся…

Классификация лазеров

Основным признаком при классификации лазеров следует считать агрегатные состояния рабочего вещества. Различают газовые, жидкостные и твердотельные лазеры. В отдельную группу выделяют полупроводниковые лазеры, т.к. физические процессы, протекающие при генерации в полупроводниках, существенно отличаются от явлений, протекающих в обычных твердотельных лазерах.

В твердотельных лазерах рабочим ансамблем атомов являются примесные атомы, введенные в сравнительно небольших количествах в основную матрицу твердого тела, которая может быть как кристаллической, так и аморфной. Например, рубин представляет собой корунд Al₂O₃, в кристаллической решетке которого часть атомов Al заменена атомами Cr. Другим примером рабочего вещества является стекло (аморфное тело) с примесью неодима. Рабочими атомами в этом случае являются соответственно атомы хрома или неодима. Однако атомы неодима могут быть введены и в кристаллическое тело, как, например, в лазере на алюмоиттриевом гранате.

Инверсия в твердотельных лазерах достигается воздействием потоков фотонов соответствующей частоты на примесные атомы рабочего тела, т.е. при помощи оптической накачки, осуществляемой путем использования специальных газоразрядных ламп.

В газах могут быть использованы энергетические уровни атомов, ионов или молекул. Рабочие уровни ионов располагаются на энергетической диаграмме выше, чем уровни атомов, а расстояния между ними больше, поэтому излучение ионных лазеров является более коротковолновым, чем атомарных лазеров. Вероятность ионных переходов выше, чем атомных, поэтому мощность ионных лазеров выше.

В молекулярных лазерах используются энергетические уровни, соответствующие колебательным и вращательным движениям атомов и молекул. Данные уровни расположены ниже атомных уровней, и интервалы между ними значительно меньше, вследствие этого излучение молекулярных газовых лазеров более длинноволновое и соответствует инфракрасной части спектра, а КПД их много больше атомарных и ионных лазеров.

Среди газовых лазеров выделяют лазеры с однородным газом (He, Ne, Ar, Kr и т.д.) и лазеры, в которых к основному рабочему газу прибавляется примесь других газов (He- Ne) и т.д.

В большинстве газовых лазеров накачка осуществляется прохождением электрического тока через рабочий газ. При электрическом разряде в газе происходит столкновение электронов и ионов с нейтральными частицами газа, а также столкновения нейтральных частиц между собой. В результате этих столкновений при определенных условиях осуществляется инверсия, необходимая для генерации излучения.

Жидкостные лазеры делят на две группы:

- лазеры, у которых рабочим веществом являются растворы неорганических соединений;

- лазеры, у которых рабочим веществом являются растворы органических красителей.

В жидкостных лазерах инверсия осуществляется при помощи оптической накачки.

В полупроводниковых лазерах рабочим телом является кристалл полупроводника. Генерация осуществляется при рекомбинации неравновесных электронов и дырок при соответствующих переходах носителей. Полупроводниковые лазеры подразделяются на две группы. К первой группе относятся лазеры, в которых рабочим телом являются кристаллы – полупроводники, изготовленные таким образом, что одна их часть обладает электронной проводимостью (n-тип), а другая – дырочной (p-тип). При этом в p-n переходе возникает большой градиент концентрации электронов и дырок. Инверсия осуществляется при инжекции носителей тока через p-n переход под влиянием прилагаемой к кристаллу разности потенциалов. Это инжекционные лазеры.

Во второй группе лазеров рабочим телом являются кристаллы полупроводника одного типа. Возбуждение осуществляется при бомбардировке кристалла полупроводника электронным пучком, или достигается оптической накачкой.

В последнее время большое развитие получили лазеры с химической накачкой, когда инверсия возникает при той или другой химической реакции.