Вероятность события

Вероятностью появления события Аназывают отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элемен­тарных исходов.

Обозначим число благоприятствующих событию А исходов через М, а число всех исходов — N:

P(A)=M/N,

где М — целое неотрицательное число, 0 £ М £ N.

Другой тип объективной вероятности определя­ется исходя из относительной частоты (частости) появления события. Например: если некоторая фирма в течение времени провела опрос 1 000 покупателей нового сорта напитка и 20 из них оценили его как вкусный, то мы можем оценить вероятность того, что потребителям понравится новый напиток как 20/1 000 = 0,02. В этом примере 20 — это час­тота наступления события, а 20/1 000 = 0,02 — это относительная частота.

Относительной частотой событияназывается от­ношение числа испытаний т, при которых собы­тие появилось, к общему числу проведенных ис­пытаний п.

W(A) == т/п

где т — целое неотрицательное число, 0 £ т£ п.

Статистической вероятностью события Аназы­вается относительная частота (частость) этого со­бытия, вычисленная по результатам большого числа испытаний. Будем обозначать ее Р^*(А). Сле­довательно,

При очень большом числе испытаний статисти­ческая вероятность приближенно равна классичес­кой вероятности, т. е.

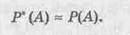
Для определения вероятности выпадения 1 или 2 при подбрасывании кости нам необходимо только знать «модель игры», в данном случае — кость с 6 гранями. Мы можем определить наши шансы теоретически, без подбрасывания кости, это априорная (доопытная) вероятность. Во втором примере мы мо­жем определить вероятность только по результатам опыта, это — апостериорная (послеопытная) веро­ятность. То есть классическая вероятность — апри­орная, а статистическая — апостериорная.

Какой бы вид вероятности ни был выбран, для их вычисления и анализа используется один и тот же набор математических правил.

Свойства вероятности, вытекающие из классического определения.

1. Вероятность достоверного события равна 1, т. е. P(W) =1.

Действительно, если событие А =W, то М = N, значит, Р(W) = N/N = 1.

2. Если событие невозможное, то его вероятность равна 0, т. е. Р(Æ)= 0.

Если А = Æ, то оно не осуществится ни при од­ном испытании, т. е. М = 0 и Р(Æ) = 0/N = 0.

3. Вероятность случайного события есть поло­жительное число, заключенное между 0 и 1, т. е. 0£ Р(А) £ 1.

4. Сумма вероятностей противоположных собы­тий равна 1, т. е. Р(А) + Р(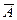) = 1. В самом деле,

Р(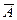) = 1 - P(A), следовательно, Р(А)+Р(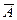)=1.

Например, если вероятность извлечения туза из колоды, состоящей из 52 карт, равна 4/52, то вероятность извлечения карты, не являющейся тузом, равна1 - 4/52=48/52

 

При нахождении вероятности классическим способом часто используются формулы комбинаторики.

2. Комбинаторика

При решении задач, заключающихся в определении вероятности, наибольшую трудность представляет подсчет общего числа элементарных исходов, общих и благоприятствующих данному событию. В этом случае полезно обратиться к формулам и правилам комбинаторики.

Комбинаторика происходит от латинского слова «combinatio» — соединение.

Группы, составленные из каких-либо предметов (например, кубиков, букв, чисел и т.п.), называются соединениями (комбинациями, подмножествами, выборками). Предметы, из которых состоят соединения, называются элементами.

Одной из задач комбинаторики является составление различных комбинаций из элементов конечного множества и изучение способов пересчета таких комбинаций, удовлетворяющих тем или иным условиям.

Условно комбинаторика делится на две части:

1) Пусть имеется n различных элементов а₁, а₂, …а_n. Каждый из этих элементов в комбинацию может войти один раз. Это комбинаторика без повторений.

2) Дано n типов элементов: «мешок» элементов типа а₁, типа а₂, типа а₃ и т.д. В каждую комбинацию может войти несколько элементов одного типа. Либо имеется n различных элементов а₁, а₂, …а_n. При этом элемент после выбора снова возвращается в группу. Это комбинаторика с повторениями.

Важнейшими характеристиками комбинаций являются: 1) состав, входящих в них элементов; 2) порядок вхождения элементов в комбинацию.

Различают три типа соединений: размещения, перестановки, сочетания.

При решении задач на нахождение количества комбинаций необходимо:

1) определить тип элементов, входящих в комбинацию;

2) определить, что нас интересует в комбинации: состав элементов, порядок их вхождения в комбинацию или и то, и другое;

3) определить тип соединения и выбрать соответствующую формулу для расчета.

При решении задач на подсчет числа комбинаций в комбинаторике применяются два правила: правило сложения и правило умножения.

Правило сложения: Если элемент А₁ может быть выбран n₁ способом, элемент А₂ – другими n₂ способами, А₃ – отличными от первых двух n₃ способами и т.д., А_к –n_k способами, отличными от первых (k-1), то выбор одного из элементов: или А₁, или А₂, или А₃, … или А_к может быть осуществлен n₁+n₂+n₃+…+А_к способами.

Правило произведения: Если элемент А₁ может быть выбран n₁ способами, после каждого такого выбора А₂ может быть выбран n₂ способами и т.д., после каждого (k-1) элемент А_k может быть выбран n_k способами, то выбор элементов А₁, А₂,…, А_к в указанном порядке может быть осуществлен n₁n₂…n_k способами.

Размещения.

Размещениями из n элементов по k в каждом называются такие комбинации, которые характеризуются и порядком и составом входящих в них элементов.

Обозначения и формулы вычисления.

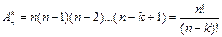- число размещений из n по k без повторений.

- число размещений из элементов n типов по k с повторениями.

Сочетания.

Сочетаниями из n элементов по k в каждом называются такие комбинации, которые характеризуются только составом входящих в них элементов.

Обозначения и формулы вычисления.

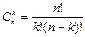, где 0≤ k ≤ n- число сочетаний из n по k без повторений.

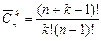- число сочетаний из элементов n типов по k с повторениями.

Перестановки.

Перестановками из n элементов называются такие комбинации, которые характеризуются только порядком входящих в них элементов при фиксированном в них составе.

Обозначения и формулы вычисления.

Число перестановок из n элементов это то же самое, что число размещений из n элементов по n в каждом, поэтому

P_n = n·(n-1)·(n-2)…2·1= n! —число перестановок из n без повторений.

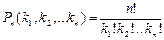- число перестановок с повторениями из k₁ элементов первого типа, k₂ элементов второго типа, … k_n элементов n типа.

Замечание.Между размещениями, сочетаниями и перестановками можно установить связь по следующей формуле

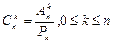
Геометрическое определение вероятности.

Пусть в результате испытания возможно бесконечное число исходов. При этом исходы несовместны и ни один из них не имеет преимущества перед другими. Для решения задачи о вероятности используется геометрическая интерпретация вероятности. В данном случае Ω представляет собой подмножество пространства R¹(числовой прямой), R²(плоскости), Rⁿ (n-мерного евклидова пространства). В пространстве R¹ в качестве подмножеств будем рассматривать лишь промежутки или их объединения, то есть подмножества, которые имеют длину, в пространстве R² — площадь, в R³ — объем и т.д.

Под мерой μ(А) подмножества А будем понимать его длину, площадь или объем в зависимости от того, какому пространству принадлежит Ω. Будем считать, что пространство элементарных исходов Ω имеет конечную меру, а вероятность попадания «случайно брошенной» точки в любое подмножество Ω пропорциональна мере этого подмножества и не зависит от его расположения и формы.

Вероятностью события А в этом случае называется число Р(А), равное отношению меры множества А к мере множества Ω:

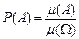
Геометрическое определение вероятности сохраняет свойства, рассмотренные в классической схеме.