Средняя геометрическая - раздел Философия, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Чтобы Получить Среднюю Геометрическую Для Группы С N Данными, Нужно Все Вариа...
Чтобы получить среднюю геометрическую для группы с n данными, нужно все варианты перемножить и из полученного произведения извлечь корень n-й степени:
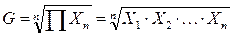 , (6.8)
, (6.8)
где:
G – средняя геометрическая;
n – число значений;
ΠXn – произведение вариантов.
Например, средняя геометрическая из 12 и 3 будет равна:
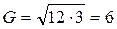 .
.
Если число значений больше двух, то извлечение корня n-й степени затруднительно, поэтому обычно значение средней геометрической находят путем логарифмирования величин, входящих в основную формулу:
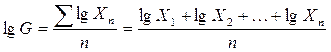 . (6.9)
. (6.9)
Например, для вариантов 1; 4; 5; 5; 5 среднюю геометрическую можно получить следующим образом:
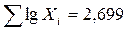 ;
;
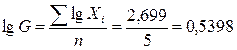 ;
;
G = 3,465.
Для проверки правильности вычисления средней геометрической можно использовать принцип единства суммарного действия. Произведение всех пяти значений (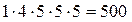 ) равно произведению пяти выровненных значений, равных средней геометрической:
) равно произведению пяти выровненных значений, равных средней геометрической:
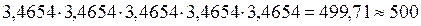 .
.
Это значит, что средняя в данном случае рассчитана правильно.
Применяется средняя геометрическая во всех случаях, когда необходимо узнать или планировать средние приросты за определенный период. При расчетах среднего попериодного прироста возможны два способа применения средней геометрической.
Первый способ применяется, когда имеются сведения о приростах за каждый период, выраженных в процентах или долях от начала каждого периода. В таких случаях расчет среднего прироста ведется по формуле:
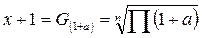 , (6.10)
, (6.10)
где:
х – средний попериодный прирост за ряд периодов равной продолжительности;
а – фактический прирост за тот или иной период, выраженный в долях;
n – число периодов;
Π(1+а) – произведение величин (1+а).
Из этой формулы следует, что для нахождения среднего прироста по первому способу нужно долю фактического прироста за каждый период прибавить к единице, полученные величины (1+а) перемножить, из их произведения извлечь корень n-й степени и вычесть единицу.
Если периодов много (n > 2), то извлечение корня надо проводить логарифмированием:
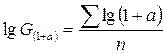 . (6.11)
. (6.11)
По этой формуле находят логарифмы средней геометрической из величин (1+a), затем находится сама величина G(1+a) и вычитанием из нее единицы получается искомая средняя доля прироста.
Пример
Поголовье бобров в заповеднике увеличилось за первый год на 5%, за второй – на 20%, за третий – на 50% и за четвертый – на 50%, считая каждый раз от начала истекшего года. Требуется определить среднегодовой прирост за эти 4 года.
Необходимые расчеты приведены в таблице 6.4.
Таблица 6.4 – Расчет среднегодового прироста
| Годы
| Фактический прирост за каждый год
| l + a
| lg(l + a)
| 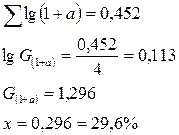
|
| %
| доля
|
|
|
| 0,05
| 1,05
| 0,021
|
|
|
| 0,20
| 1,20
| 0,079
|
|
|
| 0,50
| 1,50
| 0,176
|
|
|
| 0,50
| 1,50
| 0,176
|
Второй способ расчета средних приростов применяется в тех случаях, когда имеются данные об абсолютных количествах объектов на начало и конец общего большого периода и требуется рассчитать средний прирост за более мелкие периоды.
В таких случаях средний прирост рассчитывается по формуле:
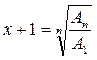 . (6.12)
. (6.12)
При логарифмировании получаем:
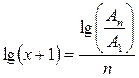 , (6.13)
, (6.13)
где:
х – средний прирост за более мелкие периоды: среднегодовой за пятилетку, среднемесячный за год, среднесуточный за месяц и т. д.;
Аn – количество объектов на конец общего периода, или, что то же самое, на конец последнего n-го мелкого периода;
А1 – количество объектов на начало исследуемого общего периода, или, что то же самое, на начало первого мелкого периода.
Пример
На пасеке на начало пятилетки было 100 ульев, а к концу стало 140. Определить среднегодовой процент увеличения пасеки за эту пятилетку. Применяя указанную формулу, получим:
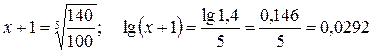 ;
;
x + 1 = 1,0697, x = 0,0697 или 6,97%
Пример
Запланировано за пять лет увеличить производство пенициллина на 60%. Требуется распределить это задание равномерно по годам. В данном случае не даны абсолютные количества в начале и в конце общего периода, но дан общий процент прироста за весь период – 60%, что дает возможность легко получить требуемое отношение 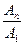 . Объем продукции должен увеличиться на 60%. Это значит, что на каждые 100 единиц, бывших в начале общего периода, должно быть 160 единиц в конце:
. Объем продукции должен увеличиться на 60%. Это значит, что на каждые 100 единиц, бывших в начале общего периода, должно быть 160 единиц в конце:
An = 160, A1 = 100, 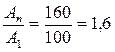
Для выполнения такого задания среднегодовой прирост производства пенициллина можно запланировать следующим образом:
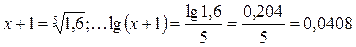 ;
;
х +1 = 1,0985, х = 0,0985, или 9,85 %.
Оказалось, что для увеличения производства за пятилетку на 60% достаточно обеспечить среднегодовой прирост на 9,85%, а не на 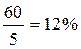 , как это могло показаться без учета того, что средний прирост образуется по принципу средней геометрической, а не средней арифметической.
, как это могло показаться без учета того, что средний прирост образуется по принципу средней геометрической, а не средней арифметической.
Все темы данного раздела:
УЧЕБНОЕ ПОСОБИЕ
для студентов вузов, обучающихся по специальности 1-31 01 01 «Биология»
Гомель 2010
Предмет и метод математической статистики
Предмет математической статистики – изучение свойств массовых явлений в биологии, экономике, технике и других областях. Эти явления обычно представляются сложными, вследствие разнообразия (варьиров
Понятие случайного события
Статистическая индукция или статистические заключения, как главная составная часть метода исследования массовых явлений, имеют свои отличительные черты. Статистические заключения делают с численно
Вероятность случайного события
Числовая характеристика случайного события, обладающая тем свойством, что для любой достаточно большой серии испытаний частота события лишь незначительно отличается от этой характеристики, называет
Вычисление вероятностей
Часто возникает необходимость одновременно складывать и умножать вероятности. Например, требуется определить вероятность выпадения 5 очков при одновременном бросании 2 кубиков. Искомая сумма вероят
Понятие случайной переменной
Определив понятие вероятности и выяснив ее главные свойства, перейдем к рассмотрению одного из важнейших понятий теории вероятностей – понятия случайной переменной.
Допустим, что в результ
Дискретные случайные переменные
Случайная переменная дискретна, если совокупность возможных ее значений конечна, или, по крайней мере, поддается счислению. Предположим, что случайная переменная X может принимать значения x1
Непрерывные случайные переменные
В противоположность дискретным случайным переменным, рассмотренным в предыдущем подразделе, совокупность возможных значений непрерывной случайной переменной не только не конечна, но и не поддается
Математическое ожидание и дисперсия
Часто возникает необходимость охарактеризовать распределение случайной переменной с помощью одного–двух числовых показателей, выражающих наиболее существенные свойства этого распределения. К таким
Моменты
Большое значение в математической статистике имеют так называемые моменты распределения случайной переменной. В математическом ожидании большие значения случайной величины учитываются недостаточно.
Биномиальное распределение и измерение вероятностей
В этой теме рассмотрим основные типы распределения дискретных случайных переменных. Предположим, что вероятность наступления некоторого случайного события А при единичном испытании равно
Прямоугольное (равномерное) распределение
Прямоугольное (равномерное) распределение — простейший тип непрерывных распределений. Если случайная переменная X может принимать любое действительное значение в интервале (а, b), где а и b – дейст
Нормальное распределение
Нормальное распределение играет основную роль в математической статистике. Это ни в малейшей степени не является случайным: в объективной действительности весьма часто встречаются различные признак
Логарифмически нормальное распределение
Случайная переменная Y имеет логарифмически нормальное распределение с параметрами μ и σ, если случайная переменная X = lnY имеет нормальное распределение с теми же параметрами μ и &
Средние величины
Из всех групповых свойств наибольшее теоретическое и практическое значение имеет средний уровень, измеряемый средней величиной признака.
Средняя величина признака – понятие очень глубокое,
Общие свойства средних величин
Для правильного использования средних величин необходимо знать свойства этих показателей: срединное расположение, абстрактность и единство суммарного действия.
По своему численному значени
Средняя арифметическая
Средняя арифметическая, обладая общими свойствами средних величин, имеет свои особенности, которые можно выразить следующими формулами:
Средний ранг (непараметрическая средняя)
Средний ранг определяется для таких признаков, для которых еще не найдены способы количественного измерения. По степени проявления таких признаков объекты могут быть ранжированы, т. е. расположены
Взвешенная средняя арифметическая
Обычно, чтобы рассчитать среднюю арифметическую, складывают все значения признака и полученную сумму делят на число вариантов. В этом случае каждое значение, входя в сумму, увеличивает ее на полную
Средняя квадратическая
Средняя квадратическая вычисляется по формуле:
, (6.5)
Она равна корню квадратному из суммы
Медиана
Медианой называют такое значение признака, которое разделяет всю группу на две равные части: одна часть имеет значения признака меньшее, чем медиана, а другая – большее.
Например, если име
Средняя гармоническая
Средняя гармоническая рассчитывается по формуле
. (6.14)
Для пяти вариантов: 1, 4, 5, 5 сре
Число степеней свободы
Число степеней свободы равно числу элементов свободного разнообразия в группе. Оно равно числу всех имеющихся элементов изучения без числа ограничений разнообразия.
Например, для исследова
Коэффициент вариации
Стандартное отклонение – величина именованная, выраженная в тех же единицах измерения, как и средняя арифметическая.
Поэтому для сравнения разных признаков, выраженных в разных единицах из
Лимиты и размах
Для быстрой и примерной оценки степени разнообразия часто применяются простейшие показатели:
lim = {min ¸ max} – лимиты, т. е. наименьшее и наибольшее значения признака,
p =
Нормированное отклонение
Обычно степень развития признака определяется путем его измерения и выражается определенным именованным числом: 3 кг веса, 15 см длины, 20 зацепок на крыле у пчел, 4% жира в молоке, 15 кг настрига
Средняя и сигма суммарной группы
Иногда бывает необходимо определить среднюю и сигму для суммарного распределения, составленного из нескольких распределений. При этом известны не сами распределения, а только их средние и сигмы.
Скошенность (асимметрия) и крутизна (эксцесс) кривой распределения
Для больших выборок (n > 100) вычисляют еще два статистических показателя.
Скошенность кривой называется асимметрией:
Вариационный ряд
По мере увеличения численности изучаемых групп все более и более проявляется та закономерность в разнообразии, которая в малочисленных группах была скрыта случайной формой своего проявления.
Гистограмма и вариационная кривая
Гистограмма – это вариационный ряд, представленный в виде диаграммы, в которой различная величина частот изображается различной высотой столбиков. Гистограмма распределения данных представлена на р
Достоверность различия распределений
Статистическая гипотеза – это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.
Проверка статистической гипотезы – это процесс принятия
Критерий по асимметрии и эксцессу
Некоторые признаки растений, животных и микроорганизмов при объединении объектов в группы дают распределения, значительно отличающиеся от нормального.
В тех случаях, когда какие-нибудь при
Генеральная совокупность и выборка
Весь массив особей определенной категории называется генеральной совокупностью. Объем генеральной совокупности определяется задачами исследования.
Если изучается какой-нибудь вид диких жив
Репрезентативность
Непосредственное изучение группы отобранных объектов дает, прежде всего, первичный материал и характеристику самой выборки.
Все выборочные данные и сводные показатели имеют значение в каче
Ошибки репрезентативности и другие ошибки исследований
Оценка генеральных параметров по выборочным показателям имеет свои особенности.
Часть никогда не может полностью охарактеризовать все целое, поэтому характеристика генеральной совокупности
Доверительные границы
Определять величину ошибок репрезентативности необходимо для того, чтобы выборочные показатели использовать еще и для нахождения возможных значений генеральных параметров. Этот процесс называется о
Общий порядок оценки
Три величины, необходимые для оценки генерального параметра, – выборочный показатель (), критерий надежности
Оценка средней арифметической
Оценка средней величины имеет целью установить величину генеральной средней для изученной категории объектов. Требуемая для этой цели ошибка репрезентативности определяется по формуле:
Оценка средней разности
В некоторых исследованиях в качестве первичных данных берется разность двух измерений. Это может быть в случае, когда каждая особь выборки изучается в двух состояниях – или в разном возрасте, или п
Недостоверная и достоверная оценка средней разности
Такие результаты выборочных исследований, по которым нельзя получить никакой определенной оценки генерального параметра (или он больше нуля, или меньше, или равен нулю), называются недостоверными.
Оценка разности генеральных средних
В биологических исследованиях особое значение имеет разность двух величин. По разности ведется сравнение разных популяций, рас, пород, сортов, линий, семейств, опытных и контрольных групп (метод гр
Критерий достоверности разности
При том большом значении, которое имеет для исследователей получение достоверных разностей, появляется необходимость овладеть методами, позволяющими определить – достоверна ли полученная, реально с
Репрезентативность при изучении качественных признаков
Качественные признаки обычно не могут иметь градаций проявления: они или имеются, или не имеются у каждой из особей, например пол, комолость, наличие или отсутствие каких-нибудь особенностей, уродс
Достоверность разности долей
Достоверность разности выборочных долей определяется так же, как и для разности средних:
(10.34)
Коэффициент корреляции
Во многих исследованиях требуется изучить несколько признаков в их взаимной связи. Если вести такое исследование по отношению к двум признакам, то можно заметить, что изменчивость одного признака н
Ошибка коэффициента корреляции
Как и всякая выборочная величина, коэффициент корреляции имеет свою ошибку репрезентативности, вычисляемую для больших выборок по формуле:
Достоверность выборочного коэффициента корреляции
Критерий выборочного коэффициента корреляции определяется по формуле:
(11.9)
где:
Доверительные границы коэффициента корреляции
Доверительные границы генерального значения коэффициента корреляции находятся общим способом по формуле:
Достоверность разности двух коэффициентов корреляции
Достоверность разности коэффициентов корреляции определяется так же, как и достоверность разности средних, по обычной формуле
Уравнение прямолинейной регрессии
Прямолинейная корреляция отличается тем, что при этой форме связи каждому из одинаковых изменений первого признака соответствует вполне определенное и тоже одинаковое в среднем изменение другого пр
Ошибки элементов уравнения прямолинейной регрессии
В уравнении простой прямолинейной регрессии:
у = а + bх
возникают три ошибки репрезентативности.
1 Ошибка коэффициента регрессии:
Частный коэффициент корреляции
Частный коэффициент корреляции – это показатель, измеряющий степень сопряженности двух признаков при постоянном значении третьего.
Математическая статистика позволяет установить корреляцию
Множественный коэффициент корреляции
Множественный коэффициент корреляции трех переменных – это показатель тесноты линейной связи между одним из признаков (буква индекса перед тире) и совокупностью двух других признаков (буквы индекса
Линейное уравнение множественной регрессии
Математическое уравнение для прямолинейной зависимости между тремя переменными называется множественным линейным уравнением плоскости регрессии. Оно имеет следующий общий вид:
Корреляционное отношение
Если связь между изучаемыми явлениями существенно отклоняется от линейной, что легко установить по графику, то коэффициент корреляции непригоден в качестве меры связи. Он может указать на отсутстви
Свойства корреляционного отношения
Корреляционное отношение измеряет степень корреляции при любой ее форме.
Кроме того, корреляционное отношение обладает рядом других свойств, представляющих большой интерес в статистическом
Ошибка репрезентативности корреляционного отношения
Еще не разработано точной формулы ошибки репрезентативности корреляционного отношения. Обычно приводимая в учебниках формула имеет недостатки, которыми не всегда можно пренебречь. Эта формула не уч
Критерий линейности корреляции
Для определения степени приближения криволинейной зависимости к прямолинейной используется критерий F, вычисляемый по формуле:
Дисперсионный комплекс
Дисперсионный комплекс – это совокупность градаций с привлеченными для исследования данными и средними из данных по каждой градации (частные средние) и по всему комплексу (общая средняя).
Статистические влияния
Статистическое влияние – это отражение в разнообразии результативного признака того разнообразия фактора (его градаций), которое организовано в исследовании.
Для оценки влияния фактора нео
Факториальное влияние
Факториальное влияние – это простое или комбинированное статистическое влияние изучаемых факторов.
В однофакторных комплексах изучается простое влияние одного фактора при определенных орга
Однофакторный дисперсионный комплекс
Дисперсионный анализ разработан и введен в практику сельскохозяйственных и биологических исследований английским ученым Р. А. Фишером, который открыл закон распределения отношения средних квадратов
Многофакторный дисперсионный комплекс
Ясное представление о математической модели дисперсионного анализа облегчает понимание необходимых вычислительных операций, особенно при обработке данных многофакторных опытов, в которых больше ист
Преобразования
Правильное использование дисперсионного анализа для обработки экспериментального материала предполагает однородность дисперсий по вариантам (выборкам), нормальное или близкое к нему распределение в
Показатели силы влияний
Определение силы влияний по их результатам требуется в биологии, сельском хозяйстве, медицине для выбора наиболее эффективных средств воздействия, для дозировки физических и химических агентов – ст
Ошибка репрезентативности основного показателя силы влияния
Точная формула ошибки основного показателя силы влияния еще не найдена.
В однофакторных комплексах, когда ошибка репрезентативности определяется только для одного показателя факториального
Предельные значения показателей силы влияния
Основной показатель силы влияния равен доле одного слагаемого от всей суммы слагаемых. Кроме того, этот показатель равен квадрату корреляционного отношения. По этим двум причинам показатель силы вл
Достоверность влияний
Основной показатель силы влияния, полученный в выборочном исследовании, характеризует, прежде всего, ту степень влияния, которая реально, в действительности, проявилась в группе исследованных объек
Дискриминантный анализ
Дискриминантный анализ является одним из методов многомерного статистического анализа. Цель дискриминантного анализа состоит в том, чтобы на основе измерения различных характеристик (признаков, пар
Постановка задачи, методы решения, ограничения
Предположим, имеется n объектов с m характеристиками. В результате измерений каждый объект характеризуется вектором x1 ... xm, m >1. Задача состоит в том, что
Предположения и ограничения
Дискриминантный анализ «работает» при выполнении ряда предположений.
Предположение о том, что наблюдаемые величины – измеряемые характеристики объекта – имеют нормальное распределение. Это
Алгоритм дискриминантного анализа
Решение задач дискриминации (дискриминантный анализ) состоит в разбиении всего выборочного пространства (множества реализации всех рассматриваемых многомерных случайных величин) на некоторое число
Кластерный анализ
Кластерный анализ объединяет различные процедуры, используемые для проведения классификации. В результате применения этих процедур исходная совокупность объектов разделяется на кластеры или группы
Методы кластерного анализа
В практике обычно реализуются агломеративные методы кластеризации.
Обычно перед началом классификации данные стандартизуются (вычитается среднее и производится деление на корень квадратный
Алгоритм кластерного анализа
Кластерный анализ – это совокупность методов классификации многомерных наблюдений или объектов, основанных на определении понятия расстояния между объектами с последующим выделением из них групп, &
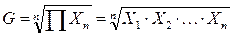 , (6.8)
, (6.8)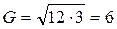 .
.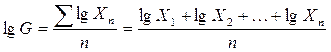 . (6.9)
. (6.9)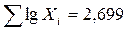 ;
;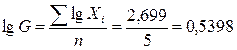 ;
;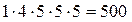 ) равно произведению пяти выровненных значений, равных средней геометрической:
) равно произведению пяти выровненных значений, равных средней геометрической: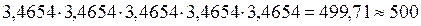 .
.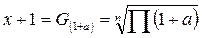 , (6.10)
, (6.10)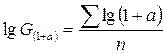 . (6.11)
. (6.11)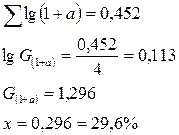
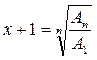 . (6.12)
. (6.12)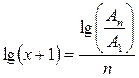 , (6.13)
, (6.13)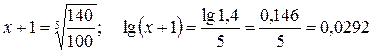 ;
;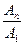 . Объем продукции должен увеличиться на 60%. Это значит, что на каждые 100 единиц, бывших в начале общего периода, должно быть 160 единиц в конце:
. Объем продукции должен увеличиться на 60%. Это значит, что на каждые 100 единиц, бывших в начале общего периода, должно быть 160 единиц в конце: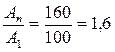
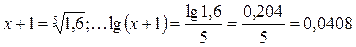 ;
;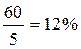 , как это могло показаться без учета того, что средний прирост образуется по принципу средней геометрической, а не средней арифметической.
, как это могло показаться без учета того, что средний прирост образуется по принципу средней геометрической, а не средней арифметической.






Новости и инфо для студентов