МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

Ю. М. ЖУЧЕНКО

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В БИОЛОГИИ И ХИМИИ

Учебное пособие

 

Гомель 2010

 

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

Ю. М. ЖУЧЕНКО

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В БИОЛОГИИ И ХИМИИ

УЧЕБНОЕ ПОСОБИЕ

    Гомель 2010

Содержание

Основные условные обозначения в математической статистике 3

Введение 8

ТЕМА 1 Основы теории вероятностей. 9

1.1 Предмет и метод математической статистики. 9

1.2 Понятие случайного события. 12

1.3 Вероятность случайного события. 15

1.4 Основные теоремы теории вероятностей. 17

ТЕМА 2 Случайные переменные. 21

2.1 Понятие случайной переменной. 21

2.2 Математическое ожидание и дисперсия. 24

2.3 Моменты 28

ТЕМА 3 Дискретные распределения. 30

3.1 Биномиальное распределение и измерение вероятностей. 30

3.2 Распределение редких событий (Пуассона) 34

ТЕМА 4 Основные модели теоретических распределений. 37

4.1 Прямоугольное (равномерное) распределение. 37

4.2 Нормальное распределение. 38

4.3 Логарифмически нормальное распределение. 43

ТЕМА 5 Распределения параметров выборки. 46

5.1 t – распределение Стьюдента. 46

5.2 F-распределение Фишера–Снедекора. 49

5.3 χ²–распределение. 50

ТЕМА 6 Основы математической статистики. 53

6.1 Средние величины.. 53

6.2 Средняя арифметическая. 57

6.3 Средняя геометрическая. 65

6.4 Средняя гармоническая. 68

ТЕМА 7 Разнообразие значений признака. 71

7.1 Стандартное (среднеквадратическое) отклонение. 71

7.2 Проверка выпадов (артефактов) 78

7.3 Средняя и сигма суммарной группы.. 79

7.4 Скошенность (асимметрия) и крутизна (эксцесс) кривой распределения 80

ТЕМА 8 Графическое представление распределений. 82

8.1 Вариационный ряд. 82

8.2 Гистограмма и вариационная кривая. 84

8.3 Кумулята 85

8.4 Достоверность различия распределений. 86

ТЕМА 9 Нормальное распределение. 93

9.1 Генеральная совокупность и выборка. 93

9.2 Репрезентативность. 96

9.3 Ошибки репрезентативности и другие ошибки исследований. 97

9.4 Доверительные границы.. 100

ТЕМА 10 Оценка генеральных параметров. 103

10.1 Общий порядок оценки. 103

10.2 Критерий достоверности разности. 113

10.3 Репрезентативность при изучении качественных признаков. 116

10.4 Достоверность разности долей. 119

ТЕМА 11 Парная корреляция. 122

11.1 Коэффициент корреляции. 122

11.2 Ошибка коэффициента корреляции. 127

11.3 Уравнение прямолинейной регрессии. 132

11.4 Ошибки элементов уравнения прямолинейной регрессии. 135

ТЕМА 12 Частная и множественная линейные корреляции и регрессии 138

12.1 Частный коэффициент корреляции. 138

12.2 Множественный коэффициент корреляции. 141

12.3 Линейное уравнение множественной регрессии. 142

ТЕМА 13 Криволинейная корреляция и регрессия. 144

13.1 Корреляционное отношение. 144

13.2 Свойства корреляционного отношения. 149

13.3 Ошибка репрезентативности корреляционного отношения. 150

13.4 Критерий линейности корреляции. 152

ТЕМА 14 Однофакторный дисперсионный анализ. 154

14.1 Сущность и метод дисперсионного анализа. 154

14.2 Однофакторный дисперсионный комплекс. 159

ТЕМА 15 Многофакторный дисперсионный анализ. 162

15.1 Многофакторный дисперсионный комплекс. 162

15.2 Преобразования. 164

15.3 Универсальное использование дисперсий. 165

ТЕМА 16 Классификация. 177

16.1 Дискриминантный анализ. 177

16.2 Кластерный анализ. 181

Литература 188

Приложение. Основные формулы и определения. 189

 

Введение

Предлагаемая работа – учебное пособие по математической статистике в биологии и химии предназначено, прежде всего, для биологов. Этим определяется как принятая в ней тематическая структура, содержание приводимых примеров, так и самый метод изложения материала. Считаясь с тем, что рядовой читатель этой книги не будет иметь математического образования, а только тот запас сведений из этой области, который дается в настоящее время в вузах с биологическим уклоном, во многих случаях сложные математические процедуры опускаются.

В ходе изложения внимание акцентируется главным образом на практическое приложение описываемых методов; упор делается также на то, чтобы выработать у читателя определенную минимальную сноровку в «арифметике» вычисления вероятностей. Если первое необходимо для осознания большой практической ценности математической статистики, то второе может весьма пригодиться при чтении научной литературы по статистике. Довольно значительное число примеров призвано облегчить понимание текста и показать некоторые основные виды проблем, решаемых с помощью математической статистики.

Главная трудность в изложении состоит в том, что в большинстве случаев выборки, с которыми имеют дело в биологических исследованиях, не складываются из независимых наблюдений, что значительно усложняет методы статистической оценки. Существует много важных биолого-экологических проблем, которые можно решить с помощью статистико-математических методов, но методы эти весьма специфичны и, как правило, сложны.

Дано достаточно традиционное изложение. При этом исключены темы, касающиеся статистики эксперимента, и в то же время сделана попытка выделить общие принципы статистической оценки.

Усвоение материала должно помочь читателю в дальнейшем самостоятельном изучении статистических методов, а также тех разделов теории операционных исследований, где рассматриваются вероятностные и статистические модели.

ТЕМА 1 Основы теории вероятностей

1.1 Предмет и метод математической статистики

1.2 Понятие случайного события

1.3 Основные теоремы теории вероятностей

Предмет и метод математической статистики

Статистическая совокупность может быть образована по одному или по нескольким признакам. Она может состоять из одной или нескольких однородных в… Теорию и методы изучения свойств массовых явлений, вычисления и анализа их… Раньше других начали изучать массовые явления в биологии, главным образом размерные характеристики человека. В 80-е…

Понятие случайного события

Основу изучения природных процессов составляет выявление причинно-следственных связей между явлениями экспериментальным путем. Осуществив по своему желанию одно или несколько первоначальных явлений (в… Например, обрабатывая семена на всхожесть определенным препаратом, экспериментатор мог поставить задачу оценить эффект…

Вероятность случайного события

Из этого рассмотрения устанавливаем, что вероятность является тем теоретическим пределом, к которому стремится частота событий при увеличении числа… Данное определение вероятности называется статистическим. Это определение не… Однако имеется и ряд положительных его свойств. Статистический подход позволяет находить вероятности событий,…

Основные теоремы теории вероятностей

Если некоторое событие может произойти при n испытаниях и
а – число исходов, которые благоприятствуют наступлению события, а b – не благоприятствуют, то вероятность того, что событие произойдет, может быть определена как р = а/n. Вероятность того, что событие не произойдет, будет: q = b/n.

Следует отметить, что слова «благоприятное» и «неблагоприятное» используются в условном смысле. Подобно этому можно было, бы сказать, что группа а содержит случаи, обладающие определенным признаком, а группа b – не обладающие. Сумма благоприятствующих и неблагоприятствующих случаев равна числу всех случаев, т. е. а+b = n. Разделив все члены этого равенства на n получим:

а/n + b/n = 1 или p +q = 1,

т. е. сумма вероятностей двух несовместных событий равна единице.

Сложение вероятностей

Если в урне с 10 шарами 6 шаров черных, 3 белых и 1 зеленый, вероятности этих событий будут равны, соответственно, 6/10, 3/10 и 1/10.

Какова вероятность вынуть белый или зеленый шар?

Благоприятствует появлению белого шара 3/10 всех исходов, а зеленого шара – 1/10 исходов. Появлению либо белого, либо зеленого шара соответствует p = 3/10 + 1/10 = 4/10 = 0,25, т. е. вероятность суммы двух несовместных (взаимоисключающих случайных) событий равна сумме их вероятностей.

Умножение вероятностей

Два события называются независимыми, когда наступление одного не оказывает влияния на наступление другого. Так, результат одного метания кости не влияет на результат следующего метания.

Вероятность сложного события (т. е. наступления двух событий независимых одно от другого равна произведению вероятностей отдельных событий.

Например, вероятность выпадения очка, а затем двух очков, при двух последовательных бросаниях кубиков, равна р = 1/6×1/6 = 1/36.

Вычисление вероятностей

кубик а 1, 2, 3, 4; кубик b 4, 3, 2, 1 Вероятность получения одного очка на кубике а равна 1/6 и получения четырех очков на кубике b – также 1/6. Вероятность…

Понятие случайной переменной

Допустим, что в результате производимого эксперимента могут наступать различные случайные события, причем наступлению каждого из них можно поставить… Один из простейших примеров случайной переменной – число очков, выпадающее при… Рассмотрим также следующий пример. Предположим, что для целей социологического исследования необходимо произвести…

Дискретные случайные переменные

, (2.1) где суммирование распространяется на все возможные значения случайной… Распределение дискретной случайной переменной можно представить двояко. Во-первых, это можно сделать в форме таблицы.…

Непрерывные случайные переменные

Из приведенных определений дискретных и непрерывных случайных переменных видно, что существует соответствие между понятиями дискретных и непрерывных… В анализе распределений вероятностей случайных переменных применяется, так… F(x) = P{X<x}

Математическое ожидание и дисперсия

Если случайная переменная X дискретна, то математическое ожидание Е(Х) этой случайной переменной определяется как сумма произведений отдельных… (2.3) Трактовка математического ожидания как некоторой стохастической (вероятностной) суммы вида (2.3), довольно обычная в…

Моменты

Начальным моментом k-го порядка случайной переменной X называется математическое ожидание k-ой степени ее: μk = Е(Хk). Центральным моментом… (2.13) В этих формулах (с, d), как и ранее, обозначает интервал, в границах которого случайная переменная X меняет свое…

Биномиальное распределение и измерение вероятностей

Примеры исчисления вероятностей можно обобщить на основе следующей ниже иллюстрации. Если подбрасываются одновременно 2 монеты (а, b), то существуют 4 возможных… аb аb аb аb

Распределение редких событий (Пуассона)

Когда вероятности альтернатив неравны, т. е. р ≠ q, биномиальное распределение асимметрично. При очень малой вероятности ожидаемого события, исчисляемой сотыми или тысячными долями единицы, по сравнению с вероятностью q противоположного события распределение вероятности или частоты таких событий описывается формулой Пуассона.

Модель такого распределения получают на основе независимых испытаний при постоянной вероятности р наступления некоторого случайного события X.

Как известно, вероятность того, что в n испытаниях случайное событие наступит равно m раз, определяется формулой, выражающей функцию распределения вероятностей для биномиального распределения.

Примем теперь дополнительные условия, а именно, что вероятность р наступления случайного события в единичном испытании весьма мала, но число испытаний n весьма велико, n , а произведение nр (обозначим его λ) – число постоянное и не очень большое.

При таких дополнительных условиях на основе формулы биноминального распределения получим следующее выражение для распределения вероятностей случайной переменной X:

(3.3)

где: λ = np; р = λ/n.

Так как числитель первой дроби имеет m сомножителей, а в знаменателе стоит nm, каждый из сомножителей можно разделить на n. Получим:

(3.4)

При nпредел любой дроби (1 – λ/n) = 1,

а предел (1 – λ/n)^n-m =e^-λ

При этих условиях:

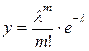(3.5)

Выражение (3.5) называется функцией распределения вероятностей в распределении Пуассона.

В этом выражении m – частота ожидаемого события в n испытаниях, е = 2,7183; параметр λ = nр равен математическому ожиданию или наиболее вероятной частоте события, , а также дисперсии.

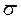Для практических расчетов, когда находят теоретические ординаты распределения n, т. е. численности распределения случайного события X, выражение (3.5) умножают на N – общее число наблюдений, вместо принимают экспериментальное среднее число наблюдаемых случаев. Формула для n будет:

(3.6)

Распределение Пуассона с возрастанием средней X приближается к биномиальному. Распределение Пуассона описывает многие явления в технике и биологии. В технике оно находит широкое применение при контроле качества продукции, для аппроксимации распределения дефектных изделий. В биологии оно применяется как модель распределения числа семян сорняков – примесей в пробных навесках при анализе семян, поврежденных вредителем. Оно описывает также распределение численности возобновления, когда размер элементарных учетных площадок очень мал или условия заселения, площади неблагоприятны, так что вероятность благоприятного исхода р мала.

 

Вопросы для самоконтроля

 

1 Что такое биномиальная кривая распределения? Какая общая формула является основой для биномиального распределения?

2 Для анализа какого вида случайных переменных используются биномиальное распределение и распределение Пуассона?

3 Что такое n в биноме (р + q)ⁿ?

4 Какими параметрами характеризуется биномиальное распределение?

5 Является ли биномиальное распределение дискретным или непрерывным?

6 Чем отличается распределение Пуассона от биномиального?

7 Какие параметры биномиального распределения можно получить с помощью треугольника Паскаля и формулы Я. Бернулли?

8 При каких условиях предпочтительнее применять распределение Пуассона?

9 При каких условиях распределение Пуассона приближается к биномиальному?

10 Какими параметрами характеризуется распределение Пуассона?

11 Что означают максимальное значение и крайние левые и правые значения на графике кривой биномиального распределения?

ТЕМА 4 Основные модели теоретических распределений

4.1 Прямоугольное (равномерное) распределение

4.2 Нормальное распределение

4.3 Логарифмически нормальное распределение

Прямоугольное (равномерное) распределение

Из приведенного определения следует, что плотность распределения вероятностей этой случайной переменной должна быть постоянной, т. е. что в… (4.1) откуда cb – са = 1 и, следовательно, получим . Таким образом, функция плотности вероятности для прямоугольного…

Нормальное распределение

Если число дискретных событий возрастает, график на рисунке 3.2, представляющий разложение бинома (p+q)n, все более приближается к плавной кривой.… В этом качестве, а именно в качестве непрерывной формы для предела…

Логарифмически нормальное распределение

Рисунок 4.2 – Кривые плотности логарифмически нормального распределения при… Если случайная переменная X имеет функцию плотности вероятности, определяемую формулой (4.6), и если X = lnY, то:

Средние величины

Средняя величина признака – понятие очень глубокое, появившееся в науке и практике только на определенном этапе развития человеческого мышления.… Средняя величина признака определяется различными способами в зависимости от… Основной показатель – средняя величина – широко используется и в науке, и в практике. При изучении растений, животных,…

Общие свойства средних величин

По своему численному значению все средние величины занимают промежуточное положение между минимальным и максимальным значениями признака. При этом… Средняя признака показывает, какую величину имел бы каждый из представителей изучаемой группы, если бы все они были…

Средняя арифметическая

, (6.2) т. е. сумма центральных отклонений равна нулю. Например, для значений 1; 4; 5; 5; 5 средняя арифметическая μ = 4.

Средний ранг (непараметрическая средняя)

Пример В зверосовхозе, разводящем голубых норок, получено от двух самцов и одной и… Таблица 6.1 – Ранжированный ряд Ранг …

Взвешенная средняя арифметическая

Средняя, рассчитанная для значений признака с неодинаковыми весами, называется взвешенной средней. Взвешенная средняя арифметическая рассчитывается… , (6.4) где:

Средняя квадратическая

, (6.5) Она равна корню квадратному из суммы квадратов данных, деленной на их число. … Например, если имеется пять вариантов: 1, 4, 5, 5, 5, то средняя квадратическая:

Мода

Модой, или модусом, называется такая варианта или класс распределения вариант, который в исследуемой группе особей встречается наиболее часто. В качестве примера рассмотрим распределение, представленное в таблице 6.2.

Таблица 6.2 – Пример распределения

Классы	100 – 119	120 – 139	140 – 159	160 – 179	180 – 199	200 – 219	220 – 239	240 – 259	260 – 279	280 – 299	300 – 319
Частоты

 

В этом распределении наиболее многочисленным является пятый класс (180 – 199) с частотой 250. Это модальный класс.

В качестве первого приближения можно принять за моду средину модального класса, т. е. 190.

Более точное значение моды можно получить по формуле:

, (6.6)

где:

М₀ – мода;

W_α – начало модального класса;

k – величина классового промежутка;

f₁ – частота класса, предшествующего модальному;

f₂ – частота модального класса;

f₃ – частота класса, следующего за модальным.

Для приведенного распределения W_α = l80, k = 20, f₁ = 160,
f₂ = 250, f₃ = 240 (таблица 6.3).

Следовательно, мода этого распределения

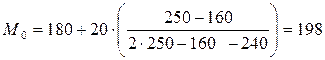
Обычно, если классы взяты не слишком мелкие, имеется всего один модальный класс.

В некоторых распределениях встречаются два или три модальных класса. Иногда это может быть следствием того, что в изучаемую группу попал разнородный материал, относящийся к разным категориям (более крупной и менее крупной) по изучаемому признаку.

Медиана

Например, если имеется группа из 9 значений признака; 1, 2, 3, 4, 5, 6, 7, 8, 9, то медианой этой группы будет 5. Для многочисленных групп медиану можно рассчитать по формуле: , (6.7)

Средняя геометрическая

, (6.8) где: G – средняя геометрическая;

Средняя гармоническая

. (6.14) Для пяти вариантов: 1, 4, 5, 5 средняя гармоническая: .

Стандартное (среднеквадратическое) отклонение

Степень разнообразия особей в группе по изучаемому признаку измеряется несколькими показателями, из которых наибольшее значение имеет стандартное отклонение или стандартное отклонение:

(7.1)

(7.2)

s – стандартное отклонение;

x² – сумма квадратов центральных отклонений, т. е. квадратов разностей между каждым значением и средней арифметической;

X_i – значение признака у каждого объекта в группе;

μ – средняя арифметическая признака для данной группы;

n – 1 – число степеней свободы, равное числу объектов в группе без одного.

Число степеней свободы

Например, для исследования требуется взять три объекта с любым развитием изучаемого признака. В данном случае величина признака не имеет никаких… Если требуется взять три числа с условием, что сумма их должна быть равна… В данном случае, при одном ограничении (сумма чисел должна быть равна 100), два числа выбираются свободно, а третье не…

Коэффициент вариации

Поэтому для сравнения разных признаков, выраженных в разных единицах измерения, используется не абсолютное, а относительное значение среднего… , (7.5) где:

Лимиты и размах

lim = {min ¸ max} – лимиты, т. е. наименьшее и наибольшее значения признака, p = (max – min) – размах, или разность между лимитами. Для группы данных 1, 2, 3, 4, 5 лимиты и размах могут быть обозначены так:

Нормированное отклонение

Задачи подобного рода возникают очень часто как в научных работах, так и в производственных условиях. Для решения таких задач применяется общий принцип: ценность особи определяется… , (7.8)

Проверка выпадов (артефактов)

Нормированное отклонение помогает определить выпады, или артефакты, т. е. такие записанные значения признака, которые резко отличаются от всех других значений признака в группе. Проверка артефактов должна проводиться всегда перед началом обработки полученных первичных данных. Если подтвердится, что резко выделяющееся значение действительно не может относиться к объектам данной группы, и попало в записи вследствие ошибок внимания, следует такой артефакт исключить из обработки.

Проверка артефактов может производиться по критерию, равному нормированному отклонению выпада:

, (7.9)

где:

Т – критерий выпада;

– выделяющееся значение признака (или очень большое или очень малое);

μ, s – средняя и сигма, рассчитанные для группы, включающей артефакт;

T_st – стандартные значения критерия выпадов, определяемых по таблице 7.3.

Таблица 7.3 – Стандартные значения критерия выпадов (T_st)

n	Tst	n	Tst	n	Tst	n	Tst
	2,0	16 – 20	2,4	47 – 66	2,8	125 – 174	3,2
3 – 4	2,1	21 – 28	2,5	67 – 84	2,9	175 – 349	3,3
5 – 9	2,2	29 – 34	2,6	85 – 104	3,0	350 – 599	3,4
10 – 15	2,3	35 – 46	2,7	105 – 124	3,1	600 – 1500	3,5

 

Если Т ≥ T_st, то анализируемое значение признака является артефактом. Альтернатива Т < T_st не позволяет исключить из анализа значение признака.

Табулированные данные таблицы 7.3 можно аппроксимировать следующей функцией: T_st = 0,287×ln(n) + 1,714

 

Пример

Данные: 1, 2, 3, 10; n = 4, μ = 4, s = 4, 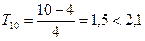; 10 еще не может считаться выпадом.

Данные: 1, 2, 2, 3, 3, 4, 4, 5, 21; n = 9, μ = 5, s = 6,1, ;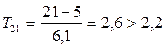

21 может считаться выпадом и должна быть исключена из обработки.

Средняя и сигма суммарной группы

Средняя и сигма в таких случаях находятся по следующим формулам: (7.10) , (7.11)

Скошенность (асимметрия) и крутизна (эксцесс) кривой распределения

Скошенность кривой называется асимметрией: (7.12) Правосторонняя асимметрия – отрицательна, левосторонняя – положительна.

Вариационный ряд

В больших группах эта закономерность проявляется уже достаточно ясно в самой форме распределения значений признака в группе. Если имеется многочисленная группа особей, то различные значения признака… В процессе изучения многих совокупностей по различным признакам наметилось несколько типов распределения признака в…

Гистограмма и вариационная кривая

На гистограмме наглядно проявляются особенности распределения. При помощи гистограмм затруднено сравнение нескольких распределений. Поэтому… Вариационная кривая – это изображение вариационного ряда в виде кривой,… На рисунке 8.2 показаны результаты опыта, в котором семена помидоров, подвергались облучению различными дозами…

Кумулята

Кумулята – это изображение распределения в виде кривой, ординаты которой пропорциональны накопленным частотам вариационного ряда. Чтобы составить ряд накопленных частот, нужно к частоте первого, наименьшего класса, прибавить частоту второго класса (S f₂ для второго класса), затем прибавить частоту третьего класса (S f₃ для третьего класса) и т. д. Кумулята для распределений веса показана на рисунке 8.3. Кумулята иногда имеет преимущество перед вариационной кривой.

 

Рисунок 8.3 – Кумулята

Некоторые методы математической статистики основаны на использовании кумуляты. К ним относятся, например, критерий лямбда и χ², определяющие достоверность различия двух распределений.

Достоверность различия распределений

Проверка статистической гипотезы – это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке… Статистический тест или статистический критерий – строгое математическое… Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии…

Критерий по асимметрии и эксцессу

В тех случаях, когда какие-нибудь причины благоприятствуют появлению значений признака, отличающихся от средней величины в сторону уменьшения или… В тех случаях, когда какие-нибудь причины благоприятствуют преимущественному… В некоторых исследованиях требуется выяснить, действительно ли распределение изучаемого признака имеет асимметрию или…

Генеральная совокупность и выборка

Если изучается какой-нибудь вид диких животных или растений, то генеральной совокупностью будут все особи этого вида. В данном случае объем… Если изучается действие какого-нибудь агента на растения и животных… Не всегда объем генеральной совокупности недоступен для сплошного исследования. Иногда изучаются небольшие…

Репрезентативность

Все выборочные данные и сводные показатели имеют значение в качестве первичных фактов, вскрытых исследованием и подлежащих тщательному рассмотрению,… То обстоятельство, что объекты отбирались в выборку специальными приемами и в… Выборка при определенных условиях становится более или менее точным отражением всей генеральной совокупности. Это…

Ошибки репрезентативности и другие ошибки исследований

Часть никогда не может полностью охарактеризовать все целое, поэтому характеристика генеральной совокупности на основе выборочного исследования… Такие ошибки являются ошибками обобщения, ошибками, связанными с перенесением… Ошибки репрезентативности в оценке генеральных параметров нельзя путать с другими видами ошибок, которые могут…

Доверительные границы

Оценка генеральных параметров не может быть выражена одним числом: это точное значение параметра остается неизвестным. Но математические методы дают… Оценка генеральных параметров по выборочным данным производится особым… Генеральный параметр может отличаться от найденного выборочного показателя не более, чем на величину возможной…

Общий порядок оценки

Выборочный показатель () рассчитывается по выборочным материалам способом, изложенным при описании этого показателя. Критерий надежности (t) определяется заранее, при планировании исследования,… Практика биологических работ выработала три основных порога вероятности безошибочных прогнозов: при обычной…

Оценка средней арифметической

(10.18) Пример При изучении шерстной продуктивности одной породы овец было взято из разных мест обитания породы у 100 взрослых овец…

Оценка средней разности

Характеристика действия определенных факторов по разности может быть произведена также и в экспериментах с аналогами, когда каждой особи в опытной… Пример При сортоиспытании пшеницы новый сорт А сравнивался со стандартным сортом В по разности урожаев, полученных на 20…

Недостоверная и достоверная оценка средней разности

Следует твердо усвоить, что недостоверные результаты выборочного исследования не дают никакого определенного ответа: ни положительного (А > В,… Очевидно, что достоверными результатами следует называть такие результаты… n = 100; n = 99;

Оценка разности генеральных средних

Если проведено сплошное исследование двух генеральных совокупностей, то разность между соответствующими средними определяется без какой бы то ни… Например, если в одном совхозе средний суточный привес каждого из… Совершенно по-другому оценивается разность между двумя выборочными средними. При анализе такой разности всегда…

Критерий достоверности разности

Достоверность выборочной разности измеряется особым показателем, который можно назвать критерием достоверности разности. Критерий достоверности разности равен отношению выборочной разности к ее… (10.20)

Репрезентативность при изучении качественных признаков

Принципиальной разницы между количественными и качественными признаками нет. Степень проявлений большинства качественных признаков при более… При изучении групповых свойств по качественным признакам характеристика группы… Основные сводные показатели: средняя величина и стандартное отклонение качественных признаков имеют, конечно, свои…

Достоверность разности долей

(10.34) где: td – критерий достоверности разности;

Коэффициент корреляции

В некоторых случаях такая зависимость проявляется настолько сильно, что при изменении первого признака на определенную величину всегда изменяется и… Встречаются функциональные связи в физических и математических обобщениях.… Необходимо учесть, что функциональные связи встречаются только в идеальных условиях, когда предполагается, что никаких…

Ошибка коэффициента корреляции

, (11.7) где – коэффициент корреляции в генеральной совокупности, из которой взята… n – численность выборки, т. е. число пар значений, по которым вычислялся выборочный коэффициент корреляции.

Достоверность выборочного коэффициента корреляции

(11.9) где: – критерий достоверности коэффициента корреляции;

Доверительные границы коэффициента корреляции

, (11.12) где: и – генеральное и выборочное значения коэффициента корреляции;

Достоверность разности двух коэффициентов корреляции

, (11.13) где: td – критерий достоверности разности коэффициентов корреляции;

Уравнение прямолинейной регрессии

Та величина, на которую в среднем изменяется второй признак, при изменении первого на единицу измерения, называется коэффициентом регрессии.… , (11.14) где R2/1 – коэффициент регрессии второго признака по первому;

Ошибки элементов уравнения прямолинейной регрессии

у = а + bх возникают три ошибки репрезентативности. 1 Ошибка коэффициента регрессии:

Частный коэффициент корреляции

Математическая статистика позволяет установить корреляцию между двумя признаками при постоянном значении третьего, не ставя специального… ; (12.1) ; (12.2)

Множественный коэффициент корреляции

; (12.6) ; (12.7) (12.8)

Линейное уравнение множественной регрессии

(12.10) Здесь Y – зависимая переменная, X и Z – независимые переменные, а – общее… Параметры а, b1 и b2 вычисляют методом наименьших квадратов, который позволяет найти такое положение плоскости…

Корреляционное отношение

Корреляционное отношение при малом числе наблюдений вычисляют по формуле: (13.1) где:

Свойства корреляционного отношения

Кроме того, корреляционное отношение обладает рядом других свойств, представляющих большой интерес в статистическом анализе корреляционных связей. … В отличие от коэффициента корреляции, который дает одинаковую меру связи…  

Ошибка репрезентативности корреляционного отношения

(13.7) Если один и тот же материал разбить по первому признаку (аргументу) на большое… В настоящее время можно использовать примерное значение ошибки не самого корреляционного отношения, а его квадрата…

Критерий линейности корреляции

(13.12) где: η2 – квадрат корреляционного отношения Y по Х;

Сущность и метод дисперсионного анализа

Сущность дисперсионного анализа заключается в изучении статистического влияния одного или нескольких факторов на результативный признак.

Результативный признак

Результативный признак (Y) – это элементарное качество или свойство объектов, изучаемое как результат влияния факторов: организованных в исследовании (X) и всех остальных, неорганизованных в данном исследовании (Z).

Результативными признаками могут быть:

- точно измеряемые особенности объектов: длина, ширина, рост, обхват, сила, резвость, шерстность, обильномолочность, содержание гемоглобина в крови, артериальное давление и т. д.;

- неточно измеряемые признаки: густота спермы в баллах, конституциональная крепость, умственные способности и т. д.;

- комбинированные признаки: отношение размеров тела, индексы продуктивности, средние из нескольких данных для одного объекта (например, средний размер клеток у каждой изучаемой особи) и т. д.;

- качественные признаки: масть, цвет глаз, болезнь, выздоровление, смерть и т. д.

Фактор

Фактор – это любое влияние, воздействие или состояние, разнообразие которых может, так или иначе, отражаться в разнообразии результативного признака.

Факторами могут быть:

- физические влияния: температура, влажность, радиационное излучение;

- химические влияния: питание, стимуляторы, мутагены, алкоголь;

- биологические влияния: здоровье и болезни, биостимуляторы, наследственность, талантливость, идиотизм;

- возраст, пол, сорт, порода, национальность;

- ареал обитания, условия жизни;

- отдельные признаки, принимаемые за аргумент при изучении других признаков – функций. Например, длина ног рысака как один из факторов, определяющих его резвость.

Градации факторов

Градации факторов – это степень их действия (нулевое действие в контрольной группе), или состояние объектов изучения (пол, возраст, обученность и т. д.).

Градациями факторов могут быть:

- разная температура, влажность, разные дозы облучения, разная продолжительность физических, воздействий;

- разные питательность и состав корма, разные дозы стимуляторов и химических мутагенов, разные стадии опьянения;

- разные периоды болезни, степени таланта, разные отцы или классы отцов, разные матери или классы матерей;

- разные возраст, пол, сорт, порода;

- разные ареалы и условия жизни;

- разная величина признака, принятого за аргумент.

Градации комплекса

Градации комплекса – это опытные группы исследования. Каждая градация комплекса соответствует одной градации фактора и включает те объекты (с их данными), которые подвергались одной степени действия фактора или находились в одном из изучаемых состояний.

Организация градаций комплекса может осуществляться разными способами: подбор опытных и контрольных групп, привлечение материалов ранее проведенных наблюдений и опытов, систематизация записей производственной отчетности.

Подбор объектов в градации из ранее намеченных генеральных совокупностей (соответствующих каждой градации) производится рендомизированно, т. е. по принципу случайной выборки, без учета развития изучаемого признака (перед отбором).

Дисперсионный комплекс

Если изучается действие одного фактора, комплекс называется однофакторным, двух факторов – двухфакторным, трех и более факторов – многофакторным. … Если во все градации подбирается одинаковое число данных, комплекс называется… Комплексы, составленные по принципу случайной выборки, называются рендомизированными.

Статистические влияния

Для оценки влияния фактора необходимо выявить разнообразие его действия, т. е. установить, насколько различно действуют его градации на… Например, для изучения влияния радиационного облучения на мутационный процесс… Если разнообразие результативного признака большое, т. е. если частота мутаций при облучении значительно отличается от…

Факториальное влияние

В однофакторных комплексах изучается простое влияние одного фактора при определенных организованных в опыте градациях и при определенных общих… Этого не следует забывать при интерпретации результатов анализа. Например,… При анализе двухфакторных дисперсионных комплексов изучаются четыре факториальных влияния.

Случайное влияние

Случайное влияние – это действие тех многих факторов, которые не организованы в изучаемом дисперсионном комплексе и составляют общий фон, на котором действуют организованные факторы. Так как неорганизованных факторов много и действуют они в разных направлениях, их влияние рассматривается как случайное, т. е. не вытекающее из закономерности действия организованных факторов.

Во всех дисперсионных комплексах случайные влияния выявляются и измеряются единообразно и для одной и той же очень важной цели: для определения той базы, с которой, как с эталоном, сравниваются факториальные влияния при определении их достоверности.

Чем больше факториальное влияние отличается от случайного, тем большая достоверность приписывается этому факториальному влиянию.

Это правило в дисперсионном анализе не имеет исключений. При определении достоверности факториальных влияний за базу сравнения можно принимать только случайные влияния.

Общее влияние

Общее влияние – это влияние всех организованных и неорганизованных факторов, определивших такое развитие признака, которое наблюдалось в дисперсионном комплексе. Общее влияние служит базой для определения доли влияний – факториальных и, случайных.

Однофакторный дисперсионный комплекс

Дисперсионный анализ широко используется для планирования эксперимента и статистической обработки его данных. Если в недалеком прошлом считали, что… При дисперсионном анализе одновременно обрабатывают данные нескольких выборок… Сущностью дисперсионного анализа является расчленение общей суммы квадратов отклонений и общего числа степеней свободы…

Многофакторный дисперсионный комплекс

CY = (СА + СВ + САB) + СZ (15.1) CY = (СА + СВ + СC + САB+ САC + СBC+ СABC) + СZ (15.2) Соответственно указанным компонентам варьирования результативного признака разлагают и общее число степеней свободы. …

Преобразования

Наиболее подходящие и чаще всего применяемые преобразования следующие: - логарифмические, когда каждое значение X трансформируется в lgX или в ln (X… - трансформация данных подсчета численности путем извлечения квадратного корня из X, т. е. или , когда некоторые…

Универсальное использование дисперсий

Все конечные результаты дисперсионного анализа можно получить без вычисления дисперсий, на основе только сумм квадратов.

Дисперсии все же приходится рассчитывать, принимая во внимание установившиеся традиции и привычную технику определения достоверности влияний.

Если в этом нет необходимости, то по одним суммам квадратов (без расчета дисперсий) можно определить:

1 показатели силы влияний;

2 ошибку репрезентативности показателя силы влияний;

3 доверительные границы генерального параметра силы влияния (приближенно);

4 показатель достоверности влияния;

5 ошибку репрезентативности частных средних по градациям дисперсионного комплекса.

Показатели силы влияний

Измерение силы статистического влияния может быть произведено при помощи квадрата корреляционного отношения, предложенного К. Пирсоном, –… Такое использование корреляционного отношения стало возможным потому, что в… При дисперсионном анализе ортогональных комплексов используются аддитивные свойства частных дисперсий (сумм квадратов…

Ошибка репрезентативности основного показателя силы влияния

В однофакторных комплексах, когда ошибка репрезентативности определяется только для одного показателя факториального влияния, удобнее пользоваться… (15.24) В двухфакторных комплексах, если рассчитаны дисперсии, можно использовать формулу:

Предельные значения показателей силы влияния

Только в единственном случае основной показатель силы влияния может получаться меньше нуля и больше единицы: при определении доверительных границ… Во всех остальных случаях (когда не определяются доверительные границы)…

Достоверность влияний

В то же время материалы выборочного комплекса, в котором определен основной показатель силы влияния, могут быть использованы также и для оценки… Оценка генерального параметра не может быть произведена путем простого… Получившееся в комплексе разнообразие частных средних никогда точно не соответствует разнообразию генеральных средних…

Дискриминантный анализ

Типичные области применения дискриминантного анализа – биология, медицина, управление производством, экономика, геология, контроль качества. В медицине объектом исследования является пациент, когда по результатам… В управлении производством принимается решение по отнесению поступающего сырья или продукции к одному из нескольких…

Постановка задачи, методы решения, ограничения

Пусть X – пространство значений вектора измерений. Решающее правило называется нерандомизированным, если пространство X разбито на k… Решающее правило называется рандомизированным, если для каждого вектора… Очевидно, при использовании решающего правила возникают потери, вызванные тем, что объект неправильно классифицирован…

Предположения и ограничения

Предположение о том, что наблюдаемые величины – измеряемые характеристики объекта – имеют нормальное распределение. Это предположение следует… Предположение об однородности дисперсий наблюдаемых переменных в разных… Методы, реализуемые в практических расчетах, являются линейными. Функции классификации и дискриминантные функции…

Алгоритм дискриминантного анализа

Пусть имеются две генеральные совокупности X и Y, имеющие многомерный (трехмерный) нормальный закон распределения с неизвестными, но равными… Из этих совокупностей взяты обучающие выборки объемами n1 и n2… ; (16.1)

Кластерный анализ

Наиболее часто методы кластерного анализа используются в социологии, маркетинговых исследованиях, экономике, биологии, медицине, археологии. Сложность задач кластерного анализа состоит в том, что реальные объекты… В целом методы кластеризации делятся на агломеративные (от слова агломерат – скопление) и итеративные дивизивные (от…

Методы кластерного анализа

Обычно перед началом классификации данные стандартизуются (вычитается среднее и производится деление на корень квадратный из дисперсии). Полученные… Можно выбрать следующие правила иерархического объединения кластеров: - метод одиночной связи,

Алгоритм кластерного анализа

Выбор конкретного метода кластерного анализа зависит от цели классификации. Кластерный анализ используется при исследовании структуры каких–либо… От матрицы исходных данных

Учебное издание

Жученко Юрий Михайлович

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В БИОЛОГИИ И ХИМИИ

Учебное пособие

для студентов вузов, обучающихся
по специальности 1-31 01 01 «Биология»

 

 

Редактор

Корректор

Лицензия _________________________

Подписано в печать . Формат 60х84 1/16.

Бумага писчая №1. Гарнитура «Таймс». Усл. п. л.

Уч.- изд. л. Тираж 100 экз. Заказ № .

 

Отпечатано с оригинала-макета на ризографе

учреждения образования

«Гомельский государственный университет

имени Франциска Скорины»

Лицензия _________________

246019, г. Гомель, ул. Советская, 104