рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Метод вращений.

Реферат Курсовая Конспект

Выберите учебное заведение

Метод вращений.

Метод вращений. - раздел Философия, Численные методы линейной алгебры Наиболее Эффективный Подход К Проблеме Собственных Значений О...

Наиболее эффективный подход к проблеме собственных значений основан на использовании преобразований подобия, позволяющих привести исходную матрицу к треугольному, диагональному или блочно-диагональному виду. Поскольку преобразование подобия не меняет спектр матрицы, то применение такого рода преобразований во многих случаях приводит к решению полной проблемы собственных значений. Наиболее эффективны преобразования подобия в случае симметричных матриц.

Однако во многих случаях достаточно предположить, что среди собственных значений матрицы отсутствуют кратные. В этом случае существует преобразование подобие, приводящее матрицу к диагональному виду.

Один из способов построения искомого преобразования подобия состоит в использовании элементарных матриц плоских вращений :

(4.10)

Матрица (для определенности пусть ) отличается от единичной матрицы только элементами и . Несложно убедиться, что матрицы являются ортогональными. В силу этого преобразования , называемое преобразованием плоских вращений, или преобразованием Гивенса, является преобразованием подобия. При умножении произвольной матрицы слева (или справа) на матрицу результирующая матрица отличается от исходной лишь элементами строк с номерам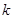и и 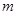(или столбцами с соответствующими номерами).

Полагая , рассмотрим произведения:

: ,

: .

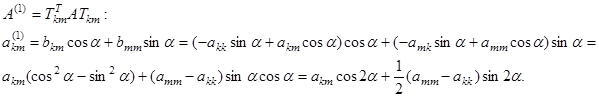
Определим угол вращения таким образом, чтобы . С учетом последнего равенства данное условие приводит к выражению для угла :

Используя тригонометрические тождества, имеем:

, . (4.11)

При выбранном угле поворота преобразование в отношении симметричной матрицы 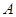обладает замечательным свойством. В результате данного преобразования уменьшается общая сумма квадратов недиагональных элементов результирующей матрицы. Многократное применение такого рода преобразования с матрицами вращения такими, что на текущем шаге приводит к сходимости последовательности матриц , к матрице диагонального вида, при этом на диагонали результирующей матрицы будут находиться приближенные значения собственных чисел исходной матрицы 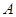. Пример реализации метода вращений в среде Matlab приведен в Приложении.

Упражнения.

1. Показать, что при умножении имеет место тождество

Развернуть

Открыть в широком формате

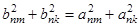– Конец работы –

Эта тема принадлежит разделу:

Численные методы линейной алгебры

В М Волков... Численные методы линейной алгебры...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод вращений.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Нормы векторов и матриц.
Поскольку численные методы по своей природе являются приближенными (по крайней мере, ввиду наличия вычислительной погрешности, обусловленной приближенностью компьютерной арифметики), важное значени

Системы линейных алгебраических уравнений. Разрешимость и устойчивость.
Решение системы линейных алгебраических уравнений для заданного вектора и квадратной матрицы

Метод Гаусса
Большинство прямых методов решения систем ЛАУ в той или иной мере наследуют идею алгоритма последовательного исключения неизвестных – метода Гаусса. Идея достаточно прозрачна. Если

Метод Гаусса с выбором ведущего элемента
При перестановке строк системы ЛАУ решение задачи не изменяться. Данное свойство лежит в основе алгоритмов упорядочения строк матрицы, позволяющих обойти некоторые недостатки метода Гаусса и повыси

LU-факторизация.
Как было показано выше, основные вычислительные затраты в методе Гаусса связаны с приведением матрицы системы ЛАУ к треугольному виду (вычислительная сложность прямого хода метода Гаусса на

Разложение Холецкого (метод квадратного корня).
В случае симметричной невырожденной матрицы есть возможность провести факторизацию более эффективно. В частности симметричную матрицу можно представить в виде произведения нижней тр

Число обусловленности матрицы и оценки погрешности решения систем линейных алгебраических уравнений.
Компьютерные вычисления являются приближенными в силу того, что действительные числа представляются конечным числом десятичных разрядов. Относительная погрешность представления действительных чисел

Свойства собственных значений и собственных векторов матриц.
Пусть дана квадратная невырожденная матрица порядка

Степенной метод.
Пусть требуется найти максимальное по абсолютной величине собственное значение матрицы , причем извест

П.1. Реализация итерационного метода вращений для расчета собственных значений симметричной матрицы
% Проблема собственных значений % Метод Вращений N=22; % Задание Размерности матрицы A=rand(N); %Формирование матрицы случайных значений A=A*A';