рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Степенной метод.

Реферат Курсовая Конспект

Выберите учебное заведение

Степенной метод.

Степенной метод. - раздел Философия, Численные методы линейной алгебры Пусть Требуется Найти Максимальное По Абсолютной Величине Соб...

Пусть требуется найти максимальное по абсолютной величине собственное значение матрицы 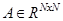, причем известно, что искомое собственное значение простое (кратности единица). Предположим, что 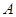– матрица простой структуры и .

Заметим, что при умножении матрицы на ее собственный вектор последний преобразуется в коллинеарный вектор 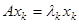, причем длина полученного при этом вектора изменяется пропорционально соответствующему собственному значению . Данное свойство собственных векторов лежит в основе степенного метода. Для матриц простой структуры система собственных векторов образует базис в пространстве 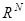, и любой вектор этого пространства может быть представлен в виде линейной комбинации векторов данного базиса.

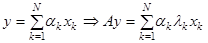
Из последнего равенства следует, что в разложении по собственным векторам при умножении матрицы на вектор наибольший рост (наименьшее убывание) испытывает составляющая, соответствующая максимальному собственному значению. Рассмотрим последовательность

. (4.6)

Поскольку то при последовательность сходится к собственному вектору . Компоненты вектора , соответствующие другим собственным значениям стремятся к нулю со скоростью геометрической прогрессии. Очевидно, что скорость сходимости последовательности определяется отношением – знаменателем геометрической прогрессии самой медленной из компонент .

Заметим, что асимптотика определяется также значением , которое в пределе стремиться к нулю или бесконечности, в зависимости от величины . В силу этого для практического использования итерационного процесса (4.6) необходима нормировка промежуточных результатов. В качестве нормировочного коэффициента наиболее походящий выбор – максимальная по абсолютной величине координата вектора :

. (4.7)

Использование итерационной процедуры (4.7) позволяет определить как собственный вектор, соответствующий максимальному собственному значению, так и величину данного собственного значения

, (4.8)

. (4.9)

После того как наибольшее собственное значение определено, данный подход может быть использован для вычисление других собственных значений и собственных векторов. Например, для вычисления наименьшего собственного значения и соответствующего ему собственного вектора процедуру (4.7)–(4.9) следует применить к матрице . В соответствии со свойством сдвига собственных значений, собственные значения матриц и 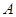связаны соотношением . В илу этого наибольшее по абсолютной величине собственное матрицы : .

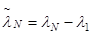Использование свойства сдвига собственных значений может оказаться очень полезным для ускорения сходимости степенного метода, когда собственные значения матрицы и близки по абсолютной величине.

К недостаткам степенного метода следует отнести тот факт, что он не может быть использован в случае, когда матрица имеет равные по модулю собственные значения. Итерационный процесс (4.7) в этом случае не сходится.

Упражнения.

1. Возможно ли с помощью степенного метода определить собственное значение действительной матрицы, если оно является комплексным?

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Численные методы линейной алгебры

В М Волков... Численные методы линейной алгебры...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Степенной метод.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Нормы векторов и матриц.
Поскольку численные методы по своей природе являются приближенными (по крайней мере, ввиду наличия вычислительной погрешности, обусловленной приближенностью компьютерной арифметики), важное значени

Системы линейных алгебраических уравнений. Разрешимость и устойчивость.
Решение системы линейных алгебраических уравнений для заданного вектора и квадратной матрицы

Метод Гаусса
Большинство прямых методов решения систем ЛАУ в той или иной мере наследуют идею алгоритма последовательного исключения неизвестных – метода Гаусса. Идея достаточно прозрачна. Если

Метод Гаусса с выбором ведущего элемента
При перестановке строк системы ЛАУ решение задачи не изменяться. Данное свойство лежит в основе алгоритмов упорядочения строк матрицы, позволяющих обойти некоторые недостатки метода Гаусса и повыси

LU-факторизация.
Как было показано выше, основные вычислительные затраты в методе Гаусса связаны с приведением матрицы системы ЛАУ к треугольному виду (вычислительная сложность прямого хода метода Гаусса на

Разложение Холецкого (метод квадратного корня).
В случае симметричной невырожденной матрицы есть возможность провести факторизацию более эффективно. В частности симметричную матрицу можно представить в виде произведения нижней тр

Число обусловленности матрицы и оценки погрешности решения систем линейных алгебраических уравнений.
Компьютерные вычисления являются приближенными в силу того, что действительные числа представляются конечным числом десятичных разрядов. Относительная погрешность представления действительных чисел

Свойства собственных значений и собственных векторов матриц.
Пусть дана квадратная невырожденная матрица порядка

Метод вращений.
Наиболее эффективный подход к проблеме собственных значений основан на использовании преобразований подобия, позволяющих привести исходную матрицу к треугольному, диагональному или

П.1. Реализация итерационного метода вращений для расчета собственных значений симметричной матрицы
% Проблема собственных значений % Метод Вращений N=22; % Задание Размерности матрицы A=rand(N); %Формирование матрицы случайных значений A=A*A';