Методические указания и контрольные работы
Вологодский государственный технический университет
Кафедра высшей математики
МАТЕМАТИЧЕСКАЯ
ЛОГИКА
Методические указания и контрольные работы
для студентов заочной формы обучения
Вологда 2011
УДК:511.147:511.61/62
Математическая логика. Контрольная работа и методические указания для студентов заочной формы обучения. – Вологда: ВоГТУ, 2011.
В методических указаниях приведены правила выполнения и оформления контрольных работ, задания для контрольных работ, образцы решения и оформления контрольных работ.
Составитель: А.Б. Назимов – канд. физ.-мат. наук, доцент
 | |||
 | |||
ПРАВИЛА ВЫПОЛНЕНИЯ
И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придерживаться указанных ниже правил.
1. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой его шифра – номера его зачетной книжки.
2. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку (чернилами синего или черного цвета).
3. Образец оформления титульного листа (обложки) тетради приведен на доске объявлений деканата ФЗДО.
4. В работу должны быть включены все задачи, указанные в задании. Работы, содержащие не все задачи задания, а также задачи не своего варианта, не рецензируются.
5. Задачи нужно решать в том порядке, в котором они указаны в контрольной работе.
6. Перед решением каждой задачи надо полностью выписать ее условие.
7. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи (рисунки).
8. Компьютерное оформление работы не рецензируется.
9. Выполненная контрольная работа сдается на кафедре в первый день зимней сессии.
Задания
для контрольных работ
 | |||
 |
Задание № 1. Даны множества
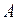 и
и 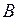 . Найти:
. Найти:
а)  , б)
, б) 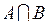 , в)
, в) 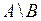 , г)
, г) 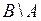 , д)
, д) 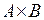 .
.
| Вариант № 6 |
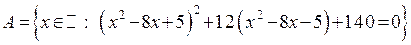 , ,
 . .
|
Задание № 2. Доказать равенство множеств.
| Вариант № 6 | 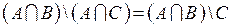 . .
|
Задание № 3. Дано бинарное отношение 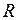 на множестве
на множестве 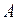 . Найти: а)
. Найти: а)  ; б)
; б) 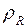 ; г)
; г) 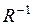 ; д)
; д) 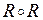 ; д)
; д) 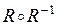 ; е)
; е) 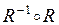 .
.
| Вариант № 6 |
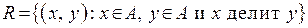 , ,  . .
|
Задание № 4. С помощью равносильных формул (элементарных тавтологий) доказать тождественно истинность данной формулы (При решении ссылаться на номер формулы из перечня равносильных формул).
| Вариант № 6 | 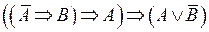 . .
|
Задание № 5. Используя основные тавтологии, построить равносильные данной формуле ДНФ и КНФ. (При решении ссылаться на номер формулы из перечня равносильных формул).
| Вариант № 6 | 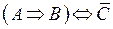 . .
|
Задание № 6. Построив таблицу истинности данной формулы, построить равносильные ей СДНФ и СКНФ.
| Вариант № 6 | 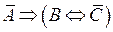 . .
|
Задание № 7. Для данной формулы алгебры высказываний построить многочлен Жегалкина.
| Вариант № 6 | 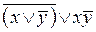 . .
|
Задание № 8. Упростить данную релейно-контактную схему.
| Вариант № 6 |
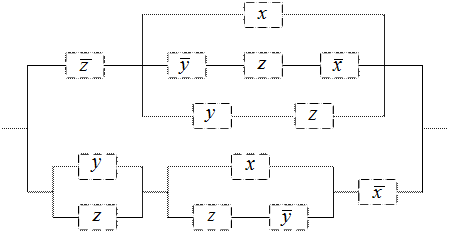
|
Образцы решения
и оформления заданий
Задание № 1.
Даны множества 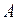 и
и 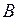 . Найти:
. Найти:
а)  , б)
, б) 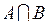 , в)
, в) 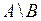 , г)
, г) 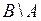 , д)
, д) 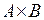 .
.
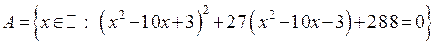 , ,
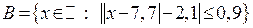 . .
|
Решение.
Решим уравнение .Задание № 2.
Доказать равенство множеств.
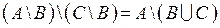 . .
|
Решение.
а) Доказательство включения :Задание № 3.
Дано бинарное отношение 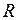 на множестве
на множестве 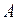 . Найти:
. Найти:
а)  ;
;
б) 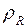 ;
;
г) 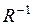 ;
;
д) 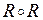 ;
;
е) 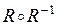 ;
;
ж) 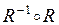 .
.
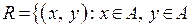 и и  делит делит 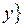 , , 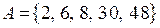 . .
|
Решение.
Решение.
;Решение.
;Решение.
Итог … Для построения СДНФ обратимся к значениям «1» в столбце «Итог». Каждому значению «1» сопоставим одну ПЭК по следующему…Решение.
Упростим данную формулу (естественно, если упрощение возвожно). Запишем данную формулу: ;Решение.
Краткий теоретический материал
Основные понятия теории множеств
Понятие множества относится к числу фундаментальных неопределяемых понятий математики. Под понятием множества будем понимать любую определенную совокупность объектов. Объекты, из которых состоит множество, называются элементами множества. Множества обозначаются заглавными латинскими буквами, а их элементы – прописными. Если объект  является элементом множества
является элементом множества 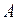 , то используется обозначение:
, то используется обозначение: 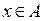 , если же объект
, если же объект  не является элементом множества
не является элементом множества 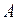 , то используется обозначение:
, то используется обозначение: 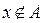 .
.
Множество, не содержащее элементов, называется пустым и обозначается 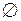 .
.
Если множество 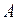 состоит из элементов
состоит из элементов 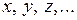 , то используется обозначение
, то используется обозначение 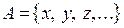 . В этом случае будем говорить, что множество задано перечислением его элементов.
. В этом случае будем говорить, что множество задано перечислением его элементов.
Обозначения для некоторых, часто используемых, множеств:
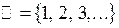
– множество натуральных чисел;
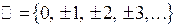
– множество целых чисел;
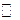 – множество вещественных чисел.
– множество вещественных чисел.
Множество можно задавать и с помощью характеристического предиката. Например, множество рациональных чисел 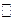 можно записать следующим образом:
можно записать следующим образом:
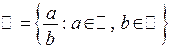 .
.
Два множества 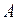 и
и 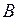 называются равными, если они состоят из одних и тех же элементов и обозначается
называются равными, если они состоят из одних и тех же элементов и обозначается  .
.
Если каждый элемент множества 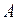 является также элементом множества
является также элементом множества 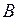 , то множество
, то множество 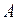 называется подмножеством множества
называется подмножеством множества 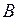 и обозначается
и обозначается  :
:
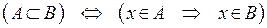 .
.
Приведем ещё одно определение равенства двух множеств 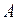 и
и 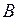 . Два множества
. Два множества 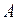 и
и 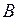 называются равными, если каждое из них являются подмножеством другого:
называются равными, если каждое из них являются подмножеством другого:
 .
.
Операции над множествами
Объединением двух множеств 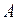 и
и 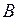 называется множество, если оно содержит только все элементы множества
называется множество, если оно содержит только все элементы множества 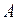 и все элементы множества
и все элементы множества 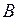 . Объединение множеств
. Объединение множеств 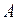 и
и 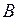 обозначается
обозначается  :
:
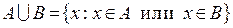 .
.
Пересечениемдвух множеств 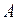 и
и 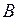 называется множество, если оно содержит только все элементы, принадлежащие множествам
называется множество, если оно содержит только все элементы, принадлежащие множествам 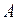 и
и 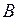 одновременно. Пересечение множеств
одновременно. Пересечение множеств 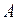 и
и 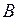 обозначается
обозначается 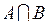 :
:
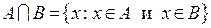 .
.
Разностью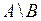 двух множеств
двух множеств 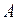 и
и 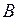 называется множество, если оно содержит только все элементы множества
называется множество, если оно содержит только все элементы множества 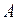 (первого множества), не принадлежащие множеству
(первого множества), не принадлежащие множеству 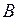 (второму множеству):
(второму множеству):
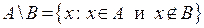 .
.