Правило дифференцирования. Таблица дифференцирования основных элементарных функций. 7
ПОСОБИЕ ПО МАТЕМАТИКЕ
ТЕМА «ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ»
СОДЕРЖАНИЕ
Введение 4
Глава 1. Производная 5
§ 1 Определение производной. 5
§ 2. Правило дифференцирования. Таблица дифференцирования основных элементарных функций. 7
§ 3.Геометрическое, механическое и экономическое приложения производной. 16
§ 4.Задачи для самостоятельной работы. 19
Глава 2 Приложения производной.21
§ 1.Дифференциал функций. 21
§ 2.Правило Лопиталя. 23
§ 3.Возрастание и убывание функций. Экстремум функции. 24
§ 4.Наибольшее и наименьшее значения функции на отрезке. 28
§ 5.Выпуклость графика функции. Точки перегиба. 29
§ 6.Исследование функций и построение их графиков. 31
§ 7.Задачи для самостоятельной работы. 36
ВВЕДЕНИЕ
Данная работа предназначена для студентов экономических специальностей ТГУСа; может быть полезна для всех категорий студентов, изучающих курс «Математика». Рассматривается раздел «Дифференциальное исчисление». В данной части излагаются темы: производная, приложение производной.
В каждом параграфе изложен теоретический материал, содержатся типовые задачи с решениями и для практических заданий, позволяющие достаточно полно охватить учебный материал. В последних параграфах каждой главы приводятся задачи для самостоятельного решения. В работе имеется подборка заданий для расчетно-графической работы по разделу «Дифференциальное исчисление». Кроме того, излагается тестовый материал для самостоятельной проверки усвоения знаний.
Пособие должно помочь студенту для самостоятельного изучения материала, когда он что-то не усвоил на практических занятиях, какие-то занятия пропустил.
Нумерация задач единая по каждой главе. Конец решения задачи обозначается знаком ►.
Глава 1. ПРОИЗВОДНАЯ
Определение производной.
Производной функциив точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю… Производную функции обозначают одним из символов . Производная функции в точке может быть вычислена по одной из формул:Функция, имеющая производную в каждой точке интервала называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
Значение производной функции 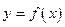 в точке
в точке 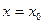 обозначается одним из символов
обозначается одним из символов 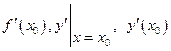
3.Если функция 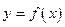 дифференцируема в точке
дифференцируема в точке 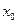 (или на множестве
(или на множестве 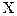 ), то она в этой точке (или на множестве
), то она в этой точке (или на множестве 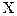 ) непрерывна. Если функция непрерывна в точке, то она не обязательно дифференцируема в этой точке.
) непрерывна. Если функция непрерывна в точке, то она не обязательно дифференцируема в этой точке.
1.1. Используя определениепроизводной,найти производную функции 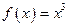 .
.
Решение. Придавая аргументу 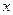 приращение
приращение 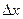 , найдем приращение функции:
, найдем приращение функции:
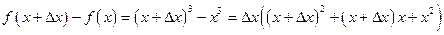 .
.
Найдем предел отношения приращения функции к приращению аргумента при 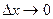 :
:
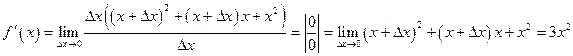 .
.
Таким образом: 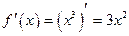 . ►
. ►
1.2.Доказать, что функция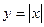 непрерывна,но не дифференцируема в точке
непрерывна,но не дифференцируема в точке 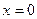 .
.
Решение.
1. Функция 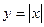 определена на всей числовой оси,причем
определена на всей числовой оси,причем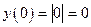 . Предел функции
. Предел функции 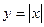 при
при 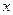 , стремящимся к нулю, равен значению функции в нуле:
, стремящимся к нулю, равен значению функции в нуле: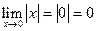 . Поэтому функция
. Поэтому функция 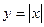 непрерывна в точке
непрерывна в точке 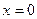
2.Составим отношение
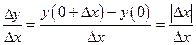
Производная функции в точке 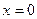
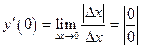 .
.
Предел зависит от знака 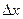 :
:
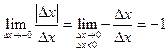 ,
,
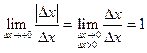
Тогда 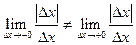 . Поэтому
. Поэтому 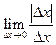 не существует и функции
не существует и функции 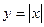 не дифференцируема в точке
не дифференцируема в точке 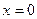 ►
►
1.3.Доказать, что функция 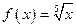 не дифференцируема в точке
не дифференцируема в точке 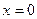 .
.
Решение. Функция 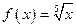 определена в любой окрестности точки
определена в любой окрестности точки 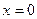 . Производная функции
. Производная функции
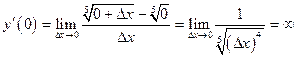
т.е. функция не является дифференцируемой в точке 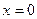 . ►
. ►
Используя определения производной, найти производную функций;
1.4.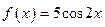 1.6.
1.6. 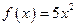
1.5. 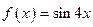 1.7.
1.7. 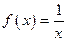
Доказать, что функция непрерывна и дифференцируема при 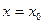
1.8.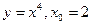 1.9.
1.9.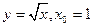
Правила дифференцирования
Таблица дифференцирования основных элементарных функций
Дифференцирование явных функций.
-постоянная, - дифференцируемые функции: (2.1) (2.2)Производная сложной функции.
Если и дифференцируемы, то (2.5) Логарифмическая производная.Логарифмическая производная используется при… .Таблица дифференцирования основных элементарных функций
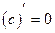 (2.7)
(2.7)
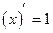 (2.8)
(2.8)
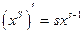 (2.9) (используем формулы
(2.9) (используем формулы 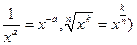
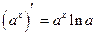 (2.10)
(2.10)
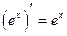 ( 2.11)
( 2.11)
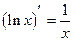 (2.12)
(2.12)
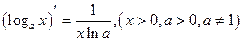 (2.13)
(2.13)
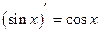 (2.14)
(2.14)
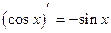 (2.15)
(2.15)
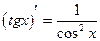 (2.16)
(2.16)
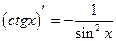 (2.17)
(2.17)
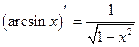 (2.18)
(2.18)
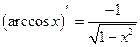 (2.19)
(2.19)
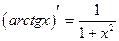 (2.20)
(2.20)
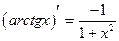 (2.21)
(2.21)
Дифференцирование неявной функции.
Если неявная функция задана уравнением , то для нахождения производной по достаточно продифференцировать это уравнение по , рассматривая при этом…Дифференцирование функций, заданных параметрически.
где - вспомогательная переменная, называемая параметром. Не выражая явноот ,… (2.22)Производные высших порядков.
(2.23) Производные порядка выше первого называются производными высших порядков.… .Геометрическое, механическое и экономическое приложения производной
1. Геометрический смысл производной.Если кривая задана уравнением 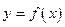 , то
, то 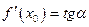 есть угловой коэффициент касательной к кривой в точке
есть угловой коэффициент касательной к кривой в точке  .
.
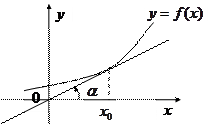 Уравнение касательной к кривой
Уравнение касательной к кривой 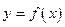 в точке
в точке 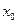 имеет вид:
имеет вид:
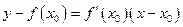 , (3.1)
, (3.1)
а уравнение нормали
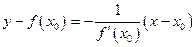 (3.2)
(3.2)
Механический смысл производной.Пусть вдоль некоторой прямой движется точка по закону , где - пройденный путь, - время. Скоростьизменения пути в момент равна . Ускорениеточки в момент равно.
3. Экономический смысл производной.Пусть 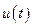 выражает объем производимой продукции за время
выражает объем производимой продукции за время 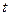 . Производная объема произведенной продукции по времени
. Производная объема произведенной продукции по времени 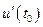 есть производительность трудав момент
есть производительность трудав момент 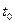 .
.
Эластичностьфункции 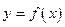 определяется с помощью соотношения
определяется с помощью соотношения
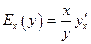 (3.3)
(3.3)
Эластичность функции приближенно показывает, на сколько процентов изменится одна переменная в результате изменения другой переменной на 1%.
Если эластичность спроса (по абсолютной величине) 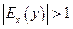 , то спрос считается эластичным, если
, то спрос считается эластичным, если 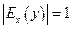 - нейтральным, если
- нейтральным, если 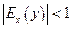 - неэластичным относительно
- неэластичным относительно 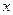 - цены (или дохода).
- цены (или дохода).
3.1.Составить уравнение касательной и нормали в точке 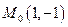 к кривой, заданной неявно
к кривой, заданной неявно 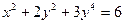 .
.
Решение. Задана точка 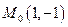 , в которой проводится касательная к кривой. Тогда,
, в которой проводится касательная к кривой. Тогда, 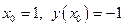 . Найдем производную неявно заданной функции:
. Найдем производную неявно заданной функции:
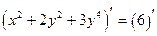 ,
,
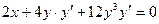 ,
,
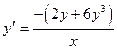 .
.
Определим производную в заданной точке:
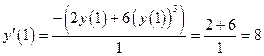 .
.
Используем уравнение касательной (3.1)
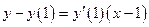 ,
,
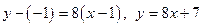
Используем уравнение нормали (3.2)
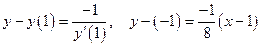
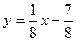 . ►
. ►
3.2.Составить уравнение касательной к графику функции 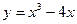 , параллельной прямой
, параллельной прямой 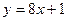 .
.
Решение. Угловой коэффициент данной прямой 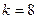 . Поэтому точка
. Поэтому точка 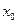 кривой
кривой 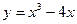 , в которой касательная параллельна данной прямой, находится из уравнения
, в которой касательная параллельна данной прямой, находится из уравнения 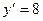 . Тогда
. Тогда 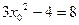 , откуда
, откуда 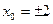 . Определяются значения функции в найденных точках:
. Определяются значения функции в найденных точках: 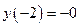 ,
, 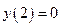 . Уравнение касательной к кривой в точке
. Уравнение касательной к кривой в точке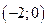 имеет вид
имеет вид
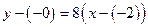 ,
,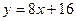
Уравнение касательной к кривой в точке 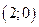 имеет вид:
имеет вид:
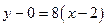 ,
, 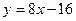 . ►
. ►
3.3.Тело движется прямолинейно по закону 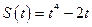 . Определить скорость и ускорения тела в момент времени
. Определить скорость и ускорения тела в момент времени 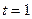
Решение. Найдем первую и вторую производную функции 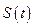 :
:
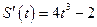 ,
, 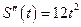 .
.
Находим скорость движения тела в момент времени 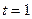 :
:
.
Определим ускорение движения тела в момент времени 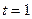
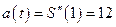 . ►
. ►
2.4.Объем производства описывается уравнением 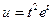 . Вычислить производительность труда в момент
. Вычислить производительность труда в момент 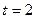
Решение. Определим производную в момент 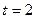 :
:
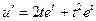 ,
, 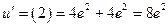 .
.
Производительность труда в момент 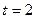 равна
равна 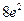 . ►
. ►
2.5. Определить эластичность функции спроса 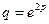 , где
, где 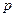 - цена единицы товара. Выяснить при каких значениях цены спрос является эластичным, нейтральным и неэластичным.
- цена единицы товара. Выяснить при каких значениях цены спрос является эластичным, нейтральным и неэластичным.
Решение. По формуле (3.3) определим эластичность 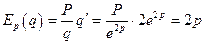 .
.
Спрос нейтрален, если 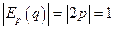 . Решая это уравнение, имеем
. Решая это уравнение, имеем 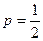 . Решение проводится при условии
. Решение проводится при условии 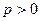 . При
. При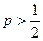 , выполняется неравенство
, выполняется неравенство 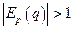 и спрос является эластичным
и спрос является эластичным 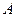 при
при 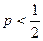 выполняется неравенство
выполняется неравенство 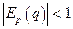 и спрос уже будет неэластичным. ►
и спрос уже будет неэластичным. ►
Составить уравнение касательной и нормали к кривой в указанных точках:
2.6. 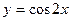
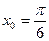
2.7. 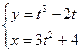
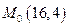
2.8. 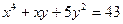
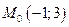
2.9. 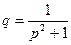
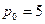
2.10. Издержки производства 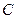 зависят от объема продукции
зависят от объема продукции 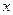 и вычисляются по формуле
и вычисляются по формуле 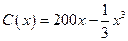 . Найти предельные издержки
. Найти предельные издержки 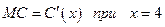 .
.
2.11.Найти эластичность функций 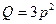 ,
, 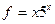
Задачи для самостоятельной работы.
1.1.; 1.3.; 1.2.; 1.4.; 2. Используя основные правила дифференцирования и таблицу дифференцирования основных элементарных функций, найти…ГЛАВА 2. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ