Понятие вектора. Линейные операции над векторами
Понятие вектора. Линейные операции над векторами.
Вектором называется направленный отрезок, имеющий определенную длину, т.е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая - за конец. Если А - начало вектора и В - его конец, то вектор обозначается символом  . Вектор можно обозначать и одной малой латинской буквой с чертой над ней (например,
. Вектор можно обозначать и одной малой латинской буквой с чертой над ней (например,  ). Изображается вектор отрезком со стрелкой на конце (рис. 24). Начало вектора называют точкой его приложения. Если точка А является началом вектора
). Изображается вектор отрезком со стрелкой на конце (рис. 24). Начало вектора называют точкой его приложения. Если точка А является началом вектора  , то мы будем говорить, что вектор приложен в точке А.
, то мы будем говорить, что вектор приложен в точке А.
Длина вектора  называется его модулем и обозначается символом
называется его модулем и обозначается символом  . Модуль вектора
. Модуль вектора  обозначается
обозначается  . Вектор
. Вектор  , для которого
, для которого  , называется единичным
, называется единичным
Вектор называется нулевым (обозначается  ), если начало и конец его совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.
), если начало и конец его совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.
Линейными операциями называются операции сложения и вычитания векторов и умножения вектора на число.
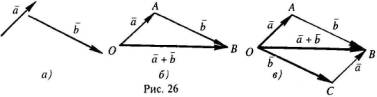
Определение. Пусть 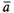 и
и  два свободных вектора (рис. 26, а). Возьмем произвольную точку О и построим вектор
два свободных вектора (рис. 26, а). Возьмем произвольную точку О и построим вектор 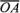 =
= 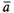 , затем от точки А отложим вектор
, затем от точки А отложим вектор  =
=  , Вектор
, Вектор  , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается
, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается  (рис. 26, б). Ту же самую сумму векторов можно получить иным способом.
(рис. 26, б). Ту же самую сумму векторов можно получить иным способом.
Отложим от точки О векторы 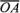 =
= 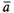 и
и  . Построим на этих векторах как на сторонах параллелограмм О ABC Вектор
. Построим на этих векторах как на сторонах параллелограмм О ABC Вектор  , служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов
, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов 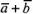 (рис. 26, в). Из рис. 26, в непосредственно следует, что сумма двух векторов обладает переместительным свойством:
(рис. 26, в). Из рис. 26, в непосредственно следует, что сумма двух векторов обладает переместительным свойством:
 .
.
Разностью 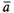 и
и  называется третий вектор
называется третий вектор  , сумма которого с вычитаемым вектором
, сумма которого с вычитаемым вектором  дает вектор
дает вектор 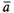 . Таким образом, если
. Таким образом, если  ,
,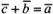 .
.
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис. 28). Откладываем векторы
 =
= 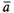 и
и  =
=  из общей точки О. Вектор
из общей точки О. Вектор 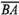 , соединяющий
, соединяющий
концы уменьшаемого вектора 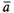 и вычитаемого вектора
и вычитаемого вектора  и направленный от вычитаемого к уменьшаемому, является разностью
и направленный от вычитаемого к уменьшаемому, является разностью  . Действительно, по правилу сложения векторов
. Действительно, по правилу сложения векторов
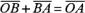 , или
, или  .
.
произведением 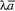 ( или
( или  )
) 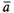 на
на  , называется вектор
, называется вектор  , коллинеарный вектору
, коллинеарный вектору 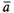 , имеющий длину, равную
, имеющий длину, равную  и то же направление, что и вектор
и то же направление, что и вектор 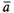 , если
, если  > 0, и направление, противоположное направление
> 0, и направление, противоположное направление  < 0. Так, например, 2
< 0. Так, например, 2 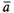 есть вектор, имеющий то же направление, что и вектор
есть вектор, имеющий то же направление, что и вектор 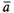 , а длину, вдвое большую, чем вектор
, а длину, вдвое большую, чем вектор 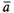 . В случае, когда
. В случае, когда  = 0 или
= 0 или 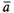 , произведение
, произведение 
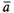 представляет собой нулевой вектор. Противоположный вектор
представляет собой нулевой вектор. Противоположный вектор можно рассматривать как результат умножения вектора
можно рассматривать как результат умножения вектора 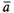 на
на 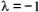
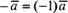
Линейные комбинации векторов.
Линейной комбинацией векторов , называется выражение вида: , где – действительные числа, называемые коэффициентами линейной комбинации. Линейная… Если , то . И наоборот, если вектор представлен в виде линейной комбинации…Коллинеарность и компланарность векторов.
Пусть — векторы пространства . Тогда верны следующие утверждения: · Если хотя бы один из трёх векторов — нулевой, то три вектора тоже считаются… · Тройка векторов, содержащая пару коллинеарных векторов, компланарна.Свойства коллинеарности
· Коллинеарность — отношение эквивалентности, то есть оно: 1. рефлексивно: 2. симметрично:Понятие базиса. Разложение вектора по базису.
Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого… Базисом в пространстве Rn называется любая система из n-линейно независимых векторов. Каждый вектор из Rn, не входящих…Скалярное произведение векторов. Свойства скалярного произведения.
Обычно используется одно из следующих обозначений: , ,Скалярное произведение векторов в декартовых координатах.
То есть, для векторов на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид , Формула скалярного произведения векторов в координатах позволяет заключить,…Векторное произведение векторов. Свойства векторного произведения.
1) Его модуль равен где - угол между векторами и . 2) Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами … 3) Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для…Векторное произведение векторов в декартовых координатах.
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисеСмешанное произведение векторов. Свойства смешанного произведения.
. Иногда его называют тройным скалярным произведением векторов, по всей… Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами…Объем пирамиды. Объем параллелепипеда.