рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Простая регрессия
Реферат Курсовая Конспект
Простая регрессия
Простая регрессия - раздел Образование, МЕТОДЫ АНАЛИЗА ДАННЫХ В Простой Линейной Регрессии Предполагается, Что Завис...
В простой линейной регрессии предполагается, что зависимая переменная 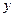 является линейной функцией
является линейной функцией  от независимой переменной
от независимой переменной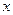 . Требуется найти значения параметров
. Требуется найти значения параметров 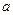 и
и 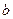 , при которых прямая
, при которых прямая  будет наилучшим образом описывать (аппроксимировать) значения переменных
будет наилучшим образом описывать (аппроксимировать) значения переменных  . Можно использовать нелинейную, например полиномиальную, регрессию, в которой предполагается, что зависимая переменная является нелинейной функцией заданной структуры с неопределенными коэффициентами (например, полиномом некоторой степени от независимой переменной). Например, полиномом второй степени будет зависимость вида
. Можно использовать нелинейную, например полиномиальную, регрессию, в которой предполагается, что зависимая переменная является нелинейной функцией заданной структуры с неопределенными коэффициентами (например, полиномом некоторой степени от независимой переменной). Например, полиномом второй степени будет зависимость вида 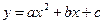 и задачей регрессии будет нахождение коэффициентов
и задачей регрессии будет нахождение коэффициентов 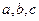 .
.
Критериями качества аппроксимации могут быть
· минимум максимальной ошибки (абсолютной или относительной),
· минимум средней ошибки (абсолютной или относительной),
· минимум среднеквадратичной ошибки (абсолютной или относительной).
Оптимизация по критерию минимума максимальной ошибки.
Для линейной регрессии для каждого номера 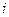 ошибка от представления значения
ошибка от представления значения  аппроксимирующей его функцией равна
аппроксимирующей его функцией равна  . Обозначим максимальную из абсолютных величин этих ошибок через
. Обозначим максимальную из абсолютных величин этих ошибок через  . Тогда
. Тогда
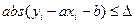 ,
,
или, что то же самое
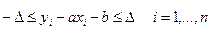 . (1)
. (1)
Условие (1) задает систему неравенств, которым должны удовлетворять неопределенные переменные 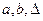 . Они должны быть выбраны так, чтобы, при выполнении условий (1) переменная
. Они должны быть выбраны так, чтобы, при выполнении условий (1) переменная  принимала минимально возможное значение:
принимала минимально возможное значение:
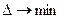 . (2)
. (2)
Такая задача является математической задачей оптимизации и решается в Excell с помощью надстройки «Поиск решения». Заметим, что она является задачей т.н. линейного программирования, что облегчает решение.
Для линейной регрессии для каждого номера 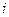 относительная ошибка имеет вид
относительная ошибка имеет вид 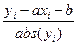 , соответственно, неравенства (1) переходят в
, соответственно, неравенства (1) переходят в
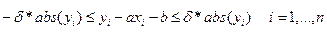 , (3)
, (3)
где через  обозначена максимальная из относительных ошибок. Построение регрессии сводится к отысканию таких значений переменных
обозначена максимальная из относительных ошибок. Построение регрессии сводится к отысканию таких значений переменных  , при которых условия (3) выполняются с наименьшим возможным значением
, при которых условия (3) выполняются с наименьшим возможным значением  :
:
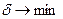 (4)
(4)
Оптимизация по критерию минимума средней ошибки.
В этом случае вместо максимальной ошибки  или
или  для каждого номера
для каждого номера 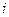 вводится в рассмотрение его ошибка
вводится в рассмотрение его ошибка 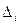 или
или 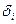 и соотношения (1), (3) заменяются на (1а) и (2а) соответственно:
и соотношения (1), (3) заменяются на (1а) и (2а) соответственно:
 , (1а)
, (1а)
 . (3а)
. (3а)
С помощью надстройки «Поиск решения» отыскиваются такие значения переменных  или
или  соответственно, которые, удовлетворяя (1а) или (3а) обеспечивают минимальное значение критериев (2а) или (4а):
соответственно, которые, удовлетворяя (1а) или (3а) обеспечивают минимальное значение критериев (2а) или (4а):
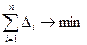 , (2а)
, (2а)
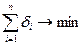 . (4а)
. (4а)
Эти задачи также являются задачами линейного программирования.
Оптимизация по критерию минимума среднеквадратичной ошибки.
В случае абсолютной ошибки среднее квадратичное отклонение 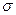 рассчитанных значений зависимой переменной от заданных равно
рассчитанных значений зависимой переменной от заданных равно
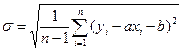 .
.
Минимизируя его, из условия равенства нулю частных производных по 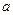 и
и 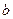 получены формулы для коэффициентов линейной регрессии:
получены формулы для коэффициентов линейной регрессии:
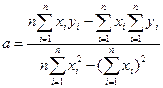 ,
,
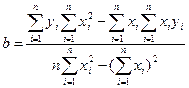 .
.
В случае относительной ошибки среднее квадратичное отклонение 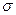 рассчитанных значений зависимой переменной от заданных равно
рассчитанных значений зависимой переменной от заданных равно
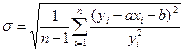 .
.
Аналогично предыдущему, из условия равенства нулю частных производных
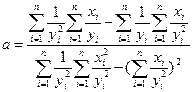
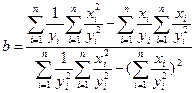
– Конец работы –
Эта тема принадлежит разделу:
МЕТОДЫ АНАЛИЗА ДАННЫХ
для выполнения исследований на младших курсах ФИСТ... С А Пиявский Несколько основных понятий математической статистики Сразу оговоримся что...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Простая регрессия
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов