ГЛАВА 1. МАТЕМАТИЧЕСКИЕ АСПЕКТ МАКРОЭКОНОМИКИ
ГЛАВА 1. МАТЕМАТИЧЕСКИЕ АСПЕКТ МАКРОЭКОНОМИКИ
Собственные значения и собственные векторы неотрицательных матриц
при этом вектор называется собственным векторомматрицы , соответствующим собственному значению . Для того, чтобы число было собственным значением матрицы , необходимо и… где - единичная матрица размеров .Определение 2.1.Величина называется мультипликатором Кейнса,а - конечным спросом.
Отсюда в силу (2.4) вытекает, что если, например, величина инвестиций возрастает на, то прирост национального дохода и прирост потребления будут… Соотношение (2.6.) показывают, что увеличение инвестиций на приведет к…Модель Хикса агрегированного рынка.
В своей знаменитой статье “Мистер Кейнс и классики” в журнале Дж. Хикс предпринял попытку объединить кейнсианский подход, считавшим основным… гдеУпражнения.
2) Показать, что при увеличении происходит увеличение и , а увеличение выпуска денег приводит к увеличению и к уменьшению реальной процентной ставки… 3) Опровергнуть (графически) парадокс вымывания инвестиции, утверждающий, по… 4) Найти равновесное состояние () в модели агрегированного рынка товаров, денег и труда, описываемого уравнениями:Модель делового цикла Самуэльсона-Хикса.
В данном параграфе мы рассмотрим динамический вариант модели Кейнса, известный под названием модели делового цикла Самульсона-Хикса. Если в модели… где - фактор акселерации, - величина инвестиций в период , - величины… Естественно также предположить, что спрос на данном этапе зависит от величины национального дохода на предыдущем…Линейная модель обмена
или в матричном виде , (5.2) где - вектор дохода от продажи. В данном пункте мы будем исходить из трех предположений.Продуктивность модели Леонтьева
Обозначим - вектор валового выпуска отраслей, - вектор конечного потребления.Модель равновесных цен.
. Разделив это равенство на , получаем ,ГЛАВА 2. МАТЕМАТИЧЕСКИЕ АСПЕКТЫ МИКРОЭКОНОМИКИ
Теория производства.
1.Пусть - производственная функция, моделирующая зависимость величины выпуска… где - цена единицы выпускаемой продукции (- функция дохода), - факторные цены.Упражнения.
2. Доказать, что линейно-однородная функция неограниченна. 3. Доказать, что частная производная однородной функции степени есть… 4. При каких условиях произведения производственных функций неоклассического типа есть неоклассическая…Математические основы теории потребления.
где - цена единицы -го товара, - величина бюджета (капитала) потребителя. Отыскание оптимального плана сводится к нахождению точки максимума функции… Из необходимого условия экстремума для функции Лагранжа следует, что (9.3)Упражнения.
2. Доказать, что задача о нахождении минимума функции расходов при фиксированном уровне функции полезности эквивалентна нахождению точки касания… 3. Доказать, что спрос нейтрален относительно (т. е. абсолютная величина… 4. Найти минимальный уровень расходов потребителя при ценах , на товары и соответственно при условии, что функция…Некоторые вопросы экономической динамики.
В данном параграфе будут рассмотрены примеры применения теории дифференциальных уравнений в непрерывных моделях экономического роста. Эти модели, в отличие от дискретных моделей, базирующихся на теории разностных уравнений, наиболее эффективны при изучении экономических систем на протяжении длительного промежутка времен.
Модель естественного роста (рост при постоянном темпе прироста).
Мы будем предполагать, что выполнена аксиома о ненасыщаемости потребителя, т.е., что весь произведенный отраслью товар будет распродан. В результате… где - норма акселерации. Подставляя в (10.2) значение из (10.1), получаем … где . Из (10.3) вытекает, что , т.е. , или (10.4)Неоклассическая модель роста.
Пусть  - национальный доход, где
- национальный доход, где 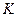 - объем капиталовложений (фондов),
- объем капиталовложений (фондов),  - величина затрат труда,
- величина затрат труда,  - линейно-однородная производственная функция
- линейно-однородная производственная функция  . Пусть
. Пусть  - производительность труда:
- производительность труда:

где 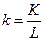 - фондовооруженность.
- фондовооруженность.
Мы будем предполагать, что:
1) Происходит естественный прирост трудовых ресурсов, т.e.

2) Инвестиции направлены как на увеличение производственных фондов, так и на амортизацию, т. e.

| (10.9) |
( - норма амортизации).
- норма амортизации).
Пусть  - норма инвестиций (т. e.
- норма инвестиций (т. e.  ), тогда
), тогда
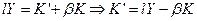 . .
| (10.10) |
Из определения фондовооруженности вытекает,
 .
.
Дифференцируя эти соотношения по  , получим
, получим
 .
.
Подставляя сюда значения для  и
и  из(10.9)и(10.10), находим
из(10.9)и(10.10), находим
 , т.е.
, т.е.  .
.
Учитывая, что  , получаем
, получаем
 . .
| (10.11) |
Уравнение (10.11) называется уравнением неоклассического роста и представляет собой дифференциальное уравнение с разделяющимися переменными.
Заметим, что если  есть корень уравнения
есть корень уравнения  , то решением уравнения при начальном условии
, то решением уравнения при начальном условии 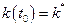 является кривая
является кривая  , которая называется стационарной кривой . Интегральная кривая уравнения (10.11) очень напоминает логистическую кривую.
, которая называется стационарной кривой . Интегральная кривая уравнения (10.11) очень напоминает логистическую кривую.
4.Пусть  - величина фондовооруженности, при которой достигается полная занятость. Найдем норму инвестиций, при которой будет сохраняться полная занятость.
- величина фондовооруженности, при которой достигается полная занятость. Найдем норму инвестиций, при которой будет сохраняться полная занятость.
Решение. Из условия задачи следует, что  , т.е.
, т.е.  .Тогда из (10.11) получаем, что
.Тогда из (10.11) получаем, что  , т.е.
, т.е.
 .
.
Упражнения.
1. Для производственной функции  найти:
найти:
а) интегральные кривые k (t) уравнения (10.11);
б) стационарную кривую;
в)  .
.
2. Пусть  - линейная производственная функция. Найти:
- линейная производственная функция. Найти:
а) интегральные кривые k (t) уравнения (10.11);
б) стационарную кривую и условия ее существования;
в)  .
.
3. Найти интегральные кривые 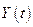 уравнения (10.8) (логистические кривые).
уравнения (10.8) (логистические кривые).
Выделить среди них стационарные и найти 
4. Пусть 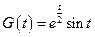 - государственные расходы,
- государственные расходы,  - потребление,
- потребление,  - норма акселерации. Найти величину государственного дохода
- норма акселерации. Найти величину государственного дохода 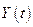 , если из- вестно, что
, если из- вестно, что  .
.
5. Найти и построить интегральные кривые уравнения (10.6) в случае, когда цена
на продукцию обратно пропорциональна количеству выпущенной продукции.
6. Найти кривые, имеющие постоянную эластичность, равную  .
.
7. Найти интегральные кривые и построить их схематический график для уравнения Самуэльсона

в случае, когда спрос и предложение - линейные функции от цены, т. е.
 .
.
Литература.
1. Макаров В. Л., Рубинов А. М., Математическая теория экономической динамики и равновесия - М., Наука, 1973.
2. Ашманов С. А. Введение в математическую экономику. - М.: Наука, 1984.
3. Аллен Р. Математическая экономия. - М.: Изд. ин. Лит.,1963.
4. Гейл Д. Теория линейных экономических моделей. - М.: Изд. ин. Лит.,1963.
5. Иванилов Ю. П., Лотов А. В. Математические модели в экономике. - М.:
Наука, 1979.
5. Ланкастер К. Математическая экономика. - М.: Сов. радио, 1972