Введение в математический анализ
Введение в математический анализ
Математический анализ (анализ бесконечно малых) изучает функции и их обобщения методом бесконечно малых величин.
В природе и технике всюду наблюдаются движения и процессы, являющиеся проявлением взаимодействия между физическими телами или средами. Математической моделью движений (т.е. переменных величин) являются функции, выражающие изменения одних величин с изменением других. Отсюда следует важность математического анализа в прикладной математике.
Основными разделами математического анализа являются: дифференциальное и интегральное исчисления.
Действительные числа
Совокупность рациональных и иррациональных чисел образует множество действительных чисел. Иррациональные числа представляются бесконечной непериодической десятичной… В то время, как рациональные числа, т.е. числа вида представляются бесконечной периодической десятичной дробью.…Числовые промежутки
1) a ≤ х ≤ b - отрезок (сегмент), обозначение - [a, b] разность b – a называется длиной отрезка; 2) a < х < b - интервал, обозначение – (a, b);Числовые последовательности
{xn} = x1, х2, …, хn Последовательность можно задать различными способами – главное, чтобы был… Например: xn = (-1)n или {xn} = -1; 1; -1; 1; …Функции одной переменной
Функциональная зависимость
Следует отметить, что функциональная зависимость является математической моделью любых процессов и явлений для детерминированных событий,… Визуализация функциональной зависимости была рассмотрена в разделе 3.7… Существуют три способа задания функций:Характеристики поведения функции
2. Пусть функция у = f (х), определена на множестве Х, тогда если для любых двух значений х1, х2 Х аргументов из неравенства х1< х2 следует… 1) f(х1) < f(х2) , то функция называется возрастающей на множестве Х. (большему значению аргумента соответствует большее значение функции);Обратная функция
Примеры: 1. Для функции обратной функцией будет ; 2. Для функции , заданной на отрезке [-1, 1] , обратной функции не существует,… Из определения обратной функции следует, что функция у = f (х) имеет обратную в том случае, если функция f (х) задаёт…Сложная функция
Например, сложная функция, определённая на множестве (-∞, 0) (-1, +∞) , так как у = f (z) = , z = φ (х) = .Основные элементарные функции
Основными элементарными функциями называют следующие функции. 1) Степенная функция , где α – действительное число. 2) Показательная функция .Предел функции
Рис. 4.1 Определение. Число А называется пределом функции f(x) при х ® а, если для любого e > 0 существует такое число…Бесконечно малые функции и их свойства
Теорема(о связимежду функцией, её пределом и бесконечно малой функцией) Для того, чтобы функция f(x) при х® а имела предел, равный А, необходимо и… f(x) = A + a(x),Бесконечно малыми.
. Графически поведение бесконечно больших функций в а при х ® а можно…Основные теоремы о пределах
Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а. Теорема 2. Доказательство теоремы. Представим f(x) = A + a(x), g(x) = B + b(x), где ,Два замечательных предела.
Первый замечательный предел.
. Доказательство. Рассмотрим в круге радиуса 1 острый угол х (МОВ), хорду МВ и… На основании предыдущего неравенства площадей имеемВторой замечательный предел
. число е иррациональное и его значение равно 2,71828… Если рассмотреть неравенствоНепрерывность функции в точке и классификация разрывов
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
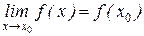 .
.
Возможны также и другие определения непрерывности функции в точке:
1) функция f(x) называется непрерывной в точке х0, если для любого положительного числа e > 0 существует такое число δ > 0, что для любых х, удовлетворяющих условию
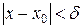
верно неравенство 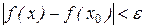 .
.
2) функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Классификация точек разрыва.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней.
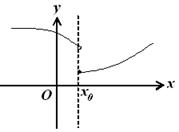
Если существует односторонний предел 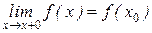 , то функция называется непрерывной справа.
, то функция называется непрерывной справа.
Если существует односторонний предел 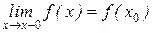 , то функция называется непрерывной слева.
, то функция называется непрерывной слева.
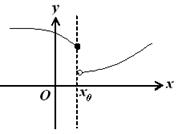
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнимости условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимойточкой разрыва.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример 1. Функция f(x) = 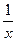 имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.  .
.

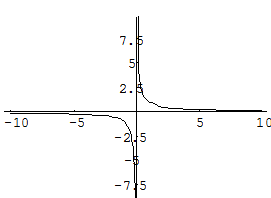
Пример 2. f(x) = 
Функция не определена в точке х = 0, но имеет в ней конечный предел 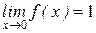 , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

График этой функции:
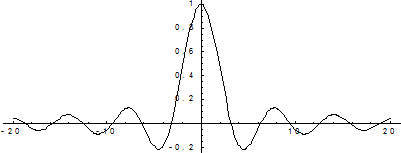
Пример 3. f(x) = 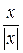 =
=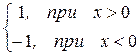
 y
y
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.