БИЛЕТ 1. Точные грани числовых множеств. Теорема существования
БИЛЕТ 1. Точные грани числовых множеств. Теорема существования.
Точной верхней гранью числового множества  (
(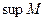 ) называется число
) называется число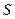 , такое что:
, такое что:
1) S- верхняя граница  (
(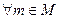
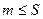 ).
).
2) Для любого положительного числа 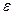 в множестве M можно найти число
в множестве M можно найти число  , такое что
, такое что
 >
>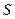 -
-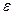 . (
. (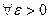
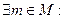
 >
>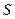 -
-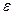 )
)
Точной нижней гранью числового множества  (
( ) называется число
) называется число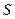 , такое что:
, такое что:
1) S- нижняя граница  (
(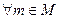
 ).
).
2) Для любого положительного числа 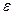 в множестве M можно найти число
в множестве M можно найти число  , такое что
, такое что

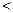
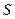 +
+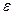 . (
. (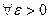
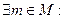

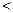
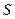 +
+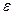 )
)
Теорема существования: Пусть 

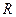 ,
, 
 , ограниченное сверху (снизу), тогда существует точная верхняя (нижняя) грань.
, ограниченное сверху (снизу), тогда существует точная верхняя (нижняя) грань.
Замечание: (аксиома непрерывности множества действительных чисел).
Пусть 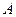

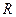 ,
, 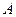
 , и
, и 

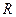 ,
, 
 , причем
, причем 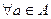 и
и  :
: 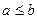 . Тогда
. Тогда
 :
: 
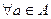 и
и  .
.


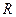 ,
, 
 , ограничено сверху.
, ограничено сверху.


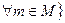 ,
,  .
.


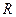 ,
,
 и
и 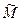

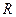 ,
, .
.
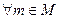 и
и 

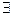
1) 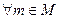
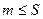
2) 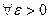
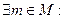
 >
>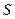 -
-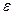
Предположим противное:
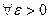 :
: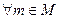 .
.

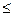
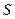 -
-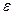
 ,
,
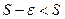 . Получили противоречие.
. Получили противоречие.
Аналогично для 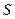 =
=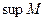 .
.
БИЛЕТ 2. Точные грани числовых множеств. Теорема единственности.
Точной верхней гранью числового множества  (
(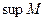 ) называется число
) называется число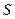 , такое что:
, такое что:
1) S- верхняя граница  (
(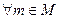
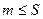 ).
).
2) Для любого положительного числа 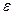 в множестве M можно найти число
в множестве M можно найти число  , такое что
, такое что
 >
>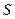 -
-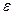 . (
. (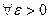
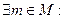
 >
>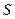 -
-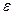 )
)
Точной нижней гранью числового множества  (
( ) называется число
) называется число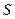 , такое что:
, такое что:
1) S- нижняя граница  (
(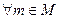
 ).
).
2) Для любого положительного числа 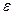 в множестве M можно найти число
в множестве M можно найти число  , такое что
, такое что

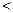
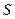 +
+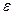 . (
. (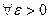
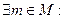

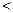
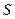 +
+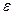 )
)
Теорема единственности: Если числовое множество  не пусто и ограничено сверху (снизу), то у него есть единственная
не пусто и ограничено сверху (снизу), то у него есть единственная 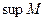 (
( ).
).
Введем следующие условия:
1) числовое множество  ограничено сверху, если можно указать такое число
ограничено сверху, если можно указать такое число  , что
, что 
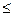
 для всех чисел
для всех чисел  из множества
из множества  .
.
2) числовое множество  ограничено снизу, если можно указать такое число
ограничено снизу, если можно указать такое число 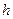 , что
, что 
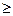
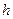 для всех чисел
для всех чисел  из множества
из множества  .
.
Доказательство:
Рассмотрим множество  , состоящее из всех чисел
, состоящее из всех чисел  , таких что для любого числа
, таких что для любого числа  из множества
из множества будет
будет 
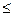
 . Такие числа
. Такие числа  существуют, так как множество
существуют, так как множество  ограничено сверху. В силу непрерывности множества действительных чисел существует такое число
ограничено сверху. В силу непрерывности множества действительных чисел существует такое число  , что
, что 
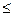
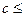
 для любых чисел
для любых чисел  (из
(из ) и
) и  (из
(из ).
).
Покажем, что  =
=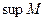 . По определению
. По определению  , для всех чисел
, для всех чисел  из множества
из множества будет
будет 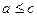 , так что первое условие выполнено. Проверим, что выполнено и второе условие. Предположим, что оно не выполнено, т.е. есть такое положительное число
, так что первое условие выполнено. Проверим, что выполнено и второе условие. Предположим, что оно не выполнено, т.е. есть такое положительное число  (
( >0), что для всех чисел
>0), что для всех чисел  из множества
из множества будет
будет  . Так как
. Так как 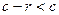 , то число
, то число 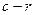 не принадлежит множеству
не принадлежит множеству  . Но это противоречит определению множества
. Но это противоречит определению множества  , которое было множеством всех чисел
, которое было множеством всех чисел  , таких что для любого числа
, таких что для любого числа  из множества
из множества будет
будет 
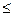
 , а мы нашли число
, а мы нашли число 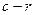 , тоже обладающее таким же свойством и не принадлежащее множеству
, тоже обладающее таким же свойством и не принадлежащее множеству  . Полученное противоречие показывает, что для числа
. Полученное противоречие показывает, что для числа  выполнено и второе условие из определения верхней грани.
выполнено и второе условие из определения верхней грани.
БИЛЕТ 3. Лемма о вложенных отрезках.
Пусть 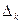 =
=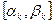 ,
, 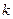 =1,2,…, причем
=1,2,…, причем 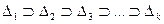 …, то есть
…, то есть 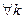
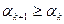 ,
,
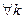
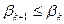 . Тогда
. Тогда 
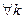 , то есть
, то есть 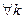
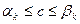 .
.
Доказательство.
а) - верхняя граница , то есть . б) - наименьшая из всех границ, то есть. .Теорема (о промежуточной последовательности).
Замечание: ().Теорема: (об отделимости от нуля).
Замечание:- ограниченная. ().Арифметика бесконечно малых последовательностей.
Пусть . Возьмем произвольный. АналогичноОграниченность.
. +Монотонность.
+.Определение: Если , то -частичный
Теорема (о частичных пределах сходящейся подпоследовательности): Пусть , тогда .Доказательство: (метод деления пополам).
ограниченная . Рассмотрим точку - середину отрезка .Т.обр.
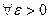


 ., то есть
., то есть 
БИЛЕТ 15. Свойства пределов функций, связанные с неравенствами.
Теорема:Пусть 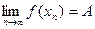 и
и  ,
,
тогда  .
.
Теорема: (Локальн. Огр.): Пусть 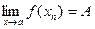 , тогда
, тогда
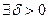 ,
,  :
: 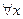

.
.
Возьмем  Тогда
Тогда 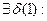
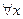
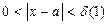 .
.

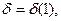
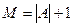
Теорема: Пусть  ,
, 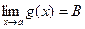 и
и 
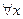
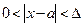
 . Тогда
. Тогда 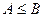
Возьмем произвольный  ,
, 
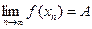 ,
,  , причем
, причем 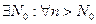
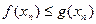 .
.

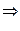 (по теореме о предельном переходе в
(по теореме о предельном переходе в
неравенство) 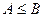 .
.
Теорема: Пусть 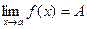 ,
, 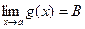 и
и

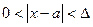
 . Тогда существует
. Тогда существует 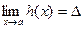 .
.
Возьмем произв.  ,
, 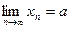
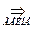
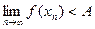 ,
,  , причем
, причем
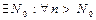
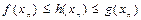

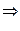 сущ.
сущ.  .
.
Теорема (об отделимости от нуля):Пусть 
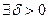 ,
,  :
: 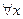
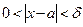
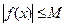 .
.
Доказательство:
.
Возьмем 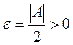 , тогда
, тогда 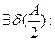
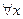
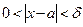
 ,
, 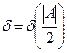 ,
,
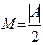 .
.
БИЛЕТ 16. Теорема об арифметике пределов функций.
Теорема: Если существуют  и
и  , то:
, то:
1). 

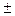
 .
.
2).  =
= (
(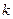 - постоянная).
- постоянная).
3).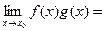
 *
* .
.
4).


 ,
,
если 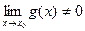 .
.
Доказательства:
Доопределив по непрерывности функции  и
и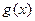
в точке  , положив
, положив 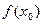 =
= и
и 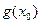 =
=
(это изменение функций не влияет на их пределы).
В точке  будут непрерывны функции
будут непрерывны функции  ,
,
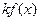 ,
,  ,
,  (так как
(так как 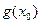
=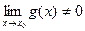 . Поэтому в силу равенства
. Поэтому в силу равенства
 =
=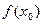 получим:
получим:
1).
 =
=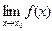
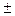
 .
.
2). =
= =
=
3).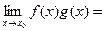
 =
= *
*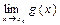 .
.
4).
 =
=

 .
.
БИЛЕТ 17. Разные виды пределов функций.
Связь предела функции в точке и односторонних пределов.
Определение: бесконечно большая при
бесконечно большая при
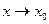 (
( ), если
), если 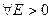

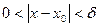
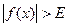 .
.
 , если
, если 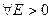
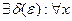
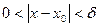
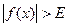 .
.
(если же 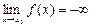 , то
, то 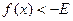 ).
).
Определение:пределы на бесконечности:
 , если
, если 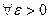
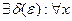

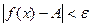 .
.
Если (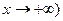 то (
то (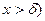
Если  то
то
Определение: односторонние пределы.
. , если .Теорема (о связи предела функции в точке