рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ПОХІДНА СКЛАДЕНОЇ ФУНКЦІЇ
Реферат Курсовая Конспект
ПОХІДНА СКЛАДЕНОЇ ФУНКЦІЇ
ПОХІДНА СКЛАДЕНОЇ ФУНКЦІЇ - раздел Математика, ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ З КУРСУ ВИЩА МАТЕМАТИКА ДО ТЕМИ ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ Похідна Складеної Функції Z = F (X, Y...
Похідна складеної функції Z = f (x, y), де x = x(t), y = y(t), t Î [t0, t1] обчислюється за допомогою формули
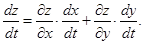 (4.17)
(4.17)
Приклад 8. Знайти 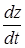 , якщо
, якщо 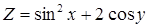 ,
, 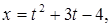
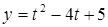 .
.
Знайдемо 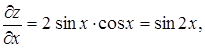
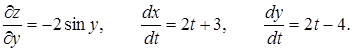
Тоді
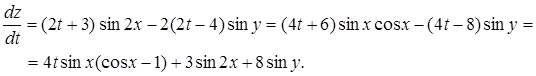
Розглянемо більш складний випадок. Нехай Z = f (x, y), а x = x(u, v),
y = y (u, v). Тоді за формулою (4.17) дістанемо
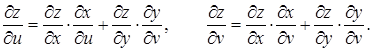 (4.18)
(4.18)
Приклад 9. Нехай 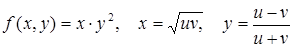 .
.
Знайти 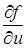 та
та 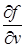 .
.
Знайдемо

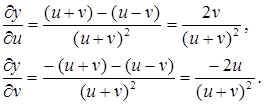
Тоді за допомогою формул (4.18) отримаємо:
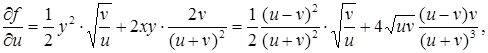
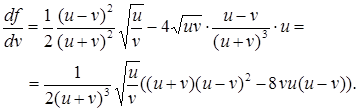
Формули (4.17), (4.18) можна узагальнити і для функцій з більшою кількістю змінних.
Відповідним чином знаходяться диференціали складених функцій.
Оскільки
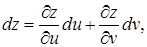
то використовуючи формули (4.18) отримаємо:
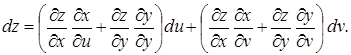
Звідки
 (4.19)
(4.19)
де 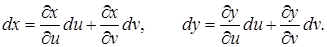
Формули (3.13) та (4.19) мають однаковий вигляд незалежно від того, будуть х та у незалежними змінними чи диференційованими функціями змінних u i v.
5. ПОХІДНА НЕЯВНОЇ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
Неявні функції можна записати у вигляді:
 (5.20)
(5.20)
Питання про існування та диференційованість неявної функції n змінних розв’язується аналогічно до того, як це було зроблено для функцій однієї змінної, де, як відомо,
 (5.21)
(5.21)
Нехай задано рівняння
F (x, y, z)=0. (5.22)
При знаходженні частинної похідної  , або
, або  величина y вважається сталою. Тому з рівняння (5.22) за допомогою (5.21) дістанемо:
величина y вважається сталою. Тому з рівняння (5.22) за допомогою (5.21) дістанемо:
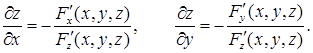 (5.23)
(5.23)
Для неявної функції (5.20) маємо:
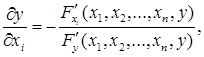 i=1,2,…,n. (5.24)
i=1,2,…,n. (5.24)
Приклад 10. Знайти частинні похідні та повний диференціал функції
Z = f (x, y), якщо
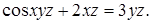
З умови отримаємо:
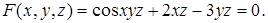
Звідси
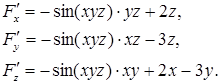
Тоді

Повний диференціал має вигляд:
 .
.
6. ПОХІДНА ЗА НАПРЯМОМ
При розв’язанні багатьох прикладних задач використовується поняття скалярного поля. Це область простору, кожній точці якої поставлено у відповідність значення деякої скалярної величини. Прикладами скалярного поля може бути поле температур тіла, поле атмосферного тиску і т. д.
Для того, щоб задати скалярне поле, досить задати скалярну функцію u(x, y, z). Поле називають стаціонарним, якщо воно не залежить від часу. Скалярне поле, яке змінюється з часом, називають нестаціонарним.
Важливою характеристикою скалярного поля є швидкість змін поля в заданому напрямі.
Нехай задано скалярне поле u = u(x, y, z). Візьмемо в ньому точку  та вектор
та вектор  , який виходить з цієї точки. Напрям
, який виходить з цієї точки. Напрям  задамо за допомогою кутів
задамо за допомогою кутів 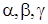 які він утворює з додатними напрямами осей координат. Візьмемо точку
які він утворює з додатними напрямами осей координат. Візьмемо точку 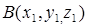 яка лежить на прямій, що проходить через А в напрямі
яка лежить на прямій, що проходить через А в напрямі  . Нехай відстань АВ дорівнює h. Тоді
. Нехай відстань АВ дорівнює h. Тоді
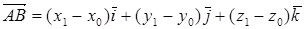
та
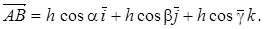
Звідси
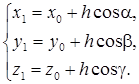
Обчислимо приріст функції u(x, y, z) при переході від А до В
 .
.
Означення 16. Якщо існує границя відношення 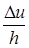 при
при  , то цю границю називають похідною функції u (x, y, z) в точці А за напрямом
, то цю границю називають похідною функції u (x, y, z) в точці А за напрямом  і позначають
і позначають 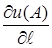 , тобто
, тобто
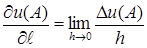 . (6.25)
. (6.25)
Зазначимо, що коли напрям  співпадає з напрямом осі Оx (
співпадає з напрямом осі Оx ( ), то границя (6.25) дорівнюватиме частинній похідній функції u за змінною х у точці А. Аналогічно, якщо
), то границя (6.25) дорівнюватиме частинній похідній функції u за змінною х у точці А. Аналогічно, якщо  співпадає з
співпадає з  , або
, або 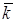 , то формула (6.25)
, то формула (6.25)
визначатиме 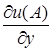 та
та 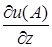 .
.
Величина 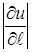 визначає величину швидкості, а знак
визначає величину швидкості, а знак 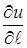 показує на зростання чи спадання величини u.
показує на зростання чи спадання величини u.
Виведемо формулу для обчислення похідної за напрямом. Користуючись виразом
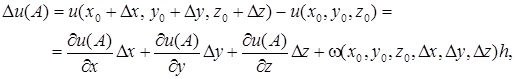
де 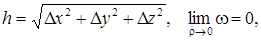 а також взявши
а також взявши 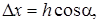
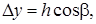
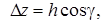 отримаємо
отримаємо
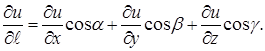 (6.26)
(6.26)
Приклад 11. Обчислити похідну функції  у точці А(1, 0, 2) у напрямку
у точці А(1, 0, 2) у напрямку 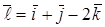 .
.
На основі (6.26) обчислимо 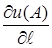 .
.
Так
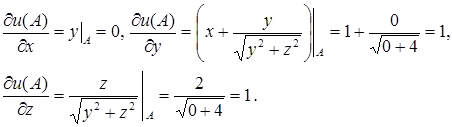
Значення 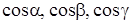 знайдемо з формул:
знайдемо з формул:
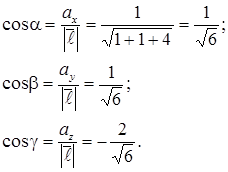
Тоді
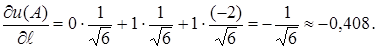
7. ГРАДІЄНТ ФУНКЦІЇ
Праву частину формули (6.26) можна розглядати як скалярний
добуток двох векторів:
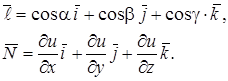
Означення 17.Вектор  називають градієнтом функції в точці А і позначають
називають градієнтом функції в точці А і позначають 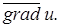 Отже
Отже
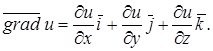 (7.27)
(7.27)
Тоді 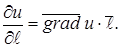 (7.28)
(7.28)
Нехай 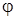 – кут між
– кут між  та
та  , тоді
, тоді 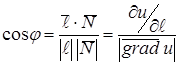 . Звідси
. Звідси 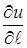 досягає максимального значення при
досягає максимального значення при  . Таким чином
. Таким чином

Це означає, що швидкість зростання скалярного поля в довільній точці є максимальною у напрямі градієнта.
Приклад 12. В якому напрямі відбувається найбільше зростання температури  у точці
у точці 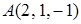 .
.
Найбільше зростання скалярного поля відбувається у напрямі вектора-градієнта, що виходить з точки А. Знайдемо 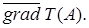 Маємо
Маємо 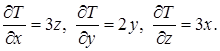 Тоді
Тоді
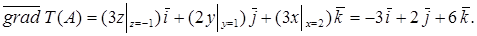
8. ДОТИЧНА ПЛОЩИНА ТА НОРМАЛЬ ДО ПОВЕРХНІ
Означення 18. Дотичною площиною до поверхні F(x;y;z)=0 у деякій її точці M0(x0;y0;z0), називається площина, яка містить усі дотичні прямі до кривих, що розташовані на даній поверхні і проходять через точку M0.
Якщо дотична площина до поверхні F(x;y;z)=0 у точці M0(x0;y0;z0) існує, то її рівняння має вигляд:
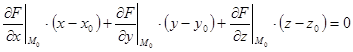 . (8.29)
. (8.29)
Означення 19. Нормаль до поверхні F(x;y;z)=0 у точці M0(x0;y0;z0) – це пряма лінія, яка проходить через точку M0(x0;y0;z0) і перпендикулярна дотичній площині до заданої поверхні у точці M0.
Якщо нормаль до поверхні F(x;y;z)=0 у точці M0(x0;y0;z0) існує, то її рівняння мають вигляд:
 (8.30)
(8.30)
Приклад 13. Скласти рівняння дотичної площини і нормалі до поверхні  у точці M0(3;4;-7).
у точці M0(3;4;-7).
Запишемо рівняння поверхні у вигляді 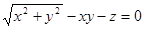 . Тоді F(x;y;z)=
. Тоді F(x;y;z)= . Знайдемо частинні похідні цієї функції:
. Знайдемо частинні похідні цієї функції:
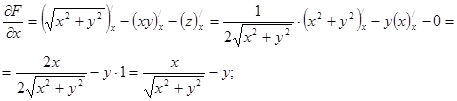
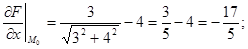
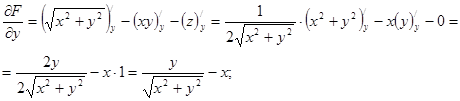
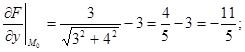
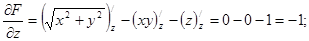
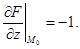
Згідно з формулою (8.29) рівняння дотичної площини має вигляд:
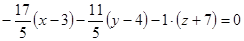 або
або 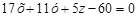 .
.
Згідно з формулою (8.30) рівняння нормалі мають вигляд:
 або
або 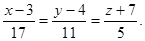
– Конец работы –
Эта тема принадлежит разделу:
ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ З КУРСУ ВИЩА МАТЕМАТИКА ДО ТЕМИ ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД... УКРАЇНСЬКИЙ ДЕРЖАВНИЙ ХІМІКО ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ... МЕТОДИЧНІ ВКАЗІВКИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ПОХІДНА СКЛАДЕНОЇ ФУНКЦІЇ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов