Выборочная функция распределения и гистограмма

 

Пусть X – некоторая случайная величина, и из этой генеральной совокупности извлечена выборка (9.1). Если элементы выборки расположить не в порядке их получения, а в порядке их возрастания

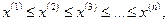(9.2)

то получаем так называемый вариационный ряд.

Известно, что приближенным значением (оценкой) вероятности события является относительная частота этого события. Следовательно, для нахождения неизвестной функции распределения 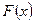генеральной совокупности нужно оценить ее значения, являющиеся вероятностью события 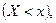с помощью относительной частоты этого события, полученной по выборке.

Определение 2. Пусть x – некоторая точка оси OX; обозначим через 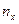– число выборочных значений из (9.2), расположенных левее точки x на той же оси. Тогда относительная частота события называется выборочной функцией распределения и обозначается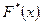

Таким образом, по определению

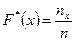(9.3)

Очевидно, что выборочная функция распределения любой случайной величины (дискретной или непрерывной) представляет всегда ступенчатую функцию, которая терпит разрывы в точках, соответствующих наблюдаемым значениям случайной величины, а величины скачков равны относительным частотам этих значений.

Пример 1. Получены результаты измерения скорости движения автомобилей на участке дороги. Данные эксперимента сведены в табл.1. Первая строка таблицы представляет собой вариационный ряд, вторая дает частоты появления каждого выборочного значения, объем выборки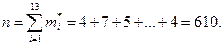

 

 

Таблица 1

Для построения выборочной функции распределения надо, согласно определению 2, вычислить относительные частоты 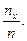Результаты вычислений представлены в табл.2.

Таблица 2
Интервал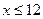
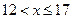
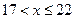
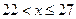
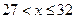
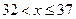
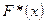
		0,007	0,019	0,027	0,053	0,104	0,161
Интервал
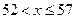
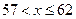
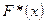
	0,23	0,409	0,642	0,826	0,944	0,993

График функции представлен на рис.1.

 

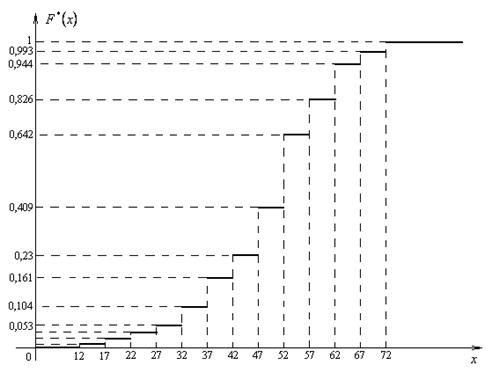
Рис.1. График выборочной функции распределения

 

Формально выборочная распределения обладает всеми свойствами теоретической функции распределения, что следует из ее определения, и отличается от нее тем, что ее значения дают не вероятности, а относительные частоты события в выборке.

Согласно теореме Бернулли, при неограниченном увеличении числа опытов n относительная частота события сходится к вероятности этого события, т.е.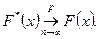

Таким образом, выборочная функция распределения 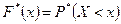является оценкой (статистическим аналогом) генеральной функции распределения 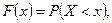и чем больше объем выборки, тем более точное представление дает выборочная функция распределения о генеральной функции распределения.

При большом числе n опытов построение выборочной функции распределения становится затруднительным. Удобнее в этом случае воспользоваться характеристиками выборочных распределений, аналогичных не функции распределения а плотности вероятности

Поступают следующим образом: делят интервал наблюдений значений случайной величины X точками на интервалы (разряды) и для каждого i-го разряда 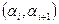вычисляют относительную частоту 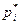попадания значений величины X в этот разряд:

(9.4)

где – число (частота) попаданий значений X в i-й разряд, 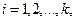n – объем выборки.

Результаты вычислений представляют в виде таблицы 3.

Таблица 3
			…		…
			…		…
			…		…

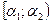
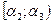
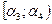
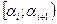
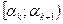
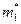
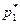
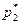
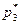
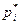
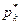
Очевидно, что

Таблицу 3 называют статистическим рядом, а графическое изображение статистического ряда называют гистограммой.

Для построения гистограммы на оси OX откладывают разряды 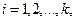и на каждом из них, как на основании, строят прямоугольник, площадь которого равна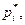 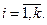Полученная при этом ступенчатая фигура 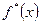называется гистограммой (рис.2).

Рис.2. Гистограмма

Очевидно, что высоты прямоугольников равны

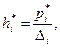(9.5)

где

Способ построения гистограммы позволяет говорить о том, что гистограмма есть оценка (приближенное изображение) генеральной функции плотности.

Согласно закону больших чисел, при 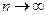и неограниченном стремлении длины интервала 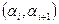к нулю функция 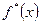сходится по вероятности к генеральной функции плотности

Число разрядов k обычно берут от 5 до 12; можно применять формулу 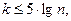где n – объем выборки, для ориентировочного определения числа k. Кроме того, в i-й разряд включают либо левую, либо правую границу интервала (см.табл.3).

Необходимо отметить, что построение гистограммы имеет смысл только для непрерывных случайных величин. Для дискретных случайных величин вместо гистограммы строят выборочный многоугольник распределения. Для построения выборочного многоугольника распределения в отличие от многоугольника распределения (см.рис.1,§7) вместо вероятностей 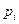берут их оценки (приближенные значения)

Пример 2. На основании статистического ряда распределения (табл.4) скоростей движения автомобилей на участке автодороги построить гистограмму.

 

Таблица 4
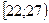
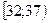
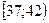
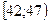
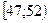
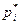
	0,004	0,022	0,095	0,138	0,21	0,178
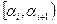
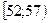
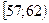
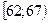
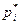
	0,199	0,095	0,034	0,0236	0,0014

Как следует из таблицы 4, объем выборки элементам (наблюдениям), 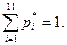Длина каждого разряда составляет 5 км. Вычислим высоты ступенек гистограммы по формуле (9.5):

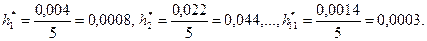
На основании этих расчетов можно строить гистограмму (рис.3).

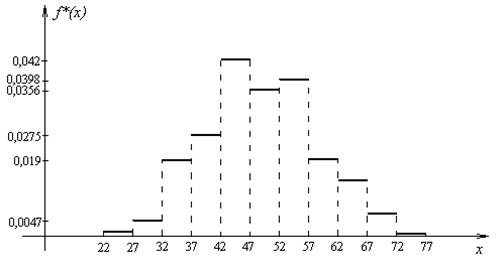
Рис.3. Гистограмма для примера 2