рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Указания к выполнению контрольной задачи Д1
Реферат Курсовая Конспект
Указания к выполнению контрольной задачи Д1
Указания к выполнению контрольной задачи Д1 - раздел Механика, Теоретическая механика. Часть 1 Задача Д1 Относится Ко Второй Основной Задаче Динамики Матери...
Задача Д1 относится ко второй основной задаче динамики материальной точки. В вариантах задач ([1],Табл. 4.2, усл. 0, 2, 4, 6, 8) сила сопротивления среды, действующая на груз, зависит от квадрата скорости груза (см. пример 4.1). В вариантах задач ([1], Табл. 4.2, усл. 1, 3, 5, 7, 9) сила сопротивления среды зависит от скорости линейно (см. пример 4.2). Задачу Д1 следует решать в следующей последовательности:
1) принять реальное тело, движение которого рассматривается в задаче, за материальную точку, наделенную массой m;
2) выбрать систему координат;
3) изобразить материальную точку в этой системе координат, определяя ее положение текущими координатами;
4) приложить к точке активные силы (т.е. силы, не зависящие от связей); если рассматривается движение несвободного тела, то в соответствии с принципом освобождаемости от связей статики приложить к материальной точке также реакции связей;
5) записать основной закон динамики точки для данной задачи;
6) проектируя векторное выражение основного закона динамики точки на выбранные оси координат, составить дифференциальные уравнения движения точки;
7) задать начальные условия движения точки;
8) проинтегрировать полученную в п. 6 систему дифференциальных уравнений;
9) используя начальные условия п. 7, определить константы интегрирования;
10) используя полученные в п. 8 уравнения движения точки, определить искомые величины.
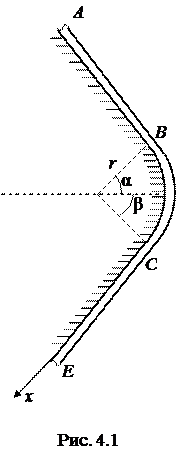 Пример 4.1. В изогнутой трубе, расположенной в вертикальной плоскости (рис. 4.1), получив в точке А начальную скорость
Пример 4.1. В изогнутой трубе, расположенной в вертикальной плоскости (рис. 4.1), получив в точке А начальную скорость  , движется груз D массой m. На прямолинейном участке трубы АВ на груз действуют сила тяжести
, движется груз D массой m. На прямолинейном участке трубы АВ на груз действуют сила тяжести 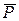 , движущая сила
, движущая сила 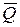 и сила сопротивления среды
и сила сопротивления среды 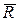 , зависящая от скорости груза. Расстояние АВ равно l. На прямолинейном участке трубы СЕ на груз действуют сила тяжести и переменная сила
, зависящая от скорости груза. Расстояние АВ равно l. На прямолинейном участке трубы СЕ на груз действуют сила тяжести и переменная сила 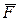 , проекция которой на ось х задана. Прямолинейные участки трубы сопряжены дугой ВС окружности радиуса r. На криволинейном участке трубы на груз действует сила тяжести. Найти:
, проекция которой на ось х задана. Прямолинейные участки трубы сопряжены дугой ВС окружности радиуса r. На криволинейном участке трубы на груз действует сила тяжести. Найти:
- скорость груза в положениях В и С;
- закон движения груза на участке СЕ.
Трением груза о трубу пренебречь.
Дано: m = 1,5 кг, Q = 7 Н, l = 2 м, V0 = 17 м/с, R = 0,3V2, Fх = – 10 sin3t, r = 0,1 м, α = 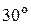 , β =
, β = 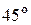 .
.
Решение. Разделим задачу на три части. Сначала определим скорость груза в точке В, рассмотрев движение груза на участке АВ. Затем, приняв скорость груза в точке В на начальную, рассмотрим движение груза на криволинейном участке ВС и определим скорость груза в точке С. Приняв эту скорость на начальную, определим уравнение движения груза на участке СЕ.
1. Определим скорость груза в точке В, рассмотрев движение груза на участке АВ. Задачу будем решать в последовательности, указанной выше. Примем груз D за материальную точку, совершающую прямолинейное движение внутри наклонного участка трубы АВ под углом 90 - a = 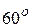 к горизонту (рис. 4.2 ).
к горизонту (рис. 4.2 ).
Направим ось z вдоль этого участка трубы, совместив начало оси с начальным положением груза в точке А. Положение материальной точки D будет определяться при прямолинейном движении координатой z.
На точку D будут действовать следующие силы: вес груза 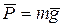 , постоянная сила
, постоянная сила 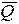 , сила сопротивления движению точки
, сила сопротивления движению точки 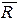 , направленная в сторону, противоположную движению, и зависящая от скорости точки V, нормальная реакция стенки трубы
, направленная в сторону, противоположную движению, и зависящая от скорости точки V, нормальная реакция стенки трубы 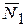 .
.
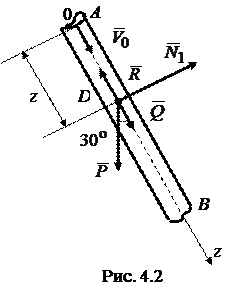 Составим основное уравнение динамики точки D:
Составим основное уравнение динамики точки D:
 +
+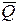 +
+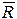 +
+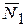 . (4.7)
. (4.7)
Проектируя (4.7) на ось z и учитывая, что 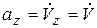 , получим дифференциальное уравнение движения точки D:
, получим дифференциальное уравнение движения точки D:
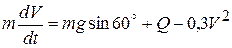 . (4.8)
. (4.8)
Запишем начальные условия:
при t = 0 z = 0, 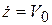 . (4.9)
. (4.9)
Принимая во внимание, что по условиям задачи для определения скорости груза в точке В дано не время движения груза на участке АВ, а длина этого участка l, перейдем от независимой переменной t к переменной z:
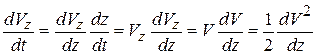 . (4.10)
. (4.10)
Подставляя (4.10) в уравнение (4.8), получим линейное уравнение первого порядка относительно квадрата скорости точки D:
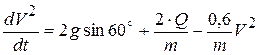 . (4.11)
. (4.11)
Обозначим
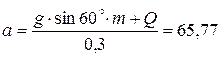 , b =
, b = 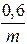 = 0,4 (4.12)
= 0,4 (4.12)
и разделим в уравнении (4.11) переменные:
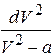 = -bdz. (4.13)
= -bdz. (4.13)
Взяв в (4.13) от обеих частей интегралы, имеем:
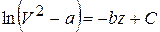 . (4.14)
. (4.14)
Определим константу интегрирования С, учитывая начальные условия (4.9):
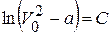 .
.
Cледовательно, ln(V2 - a) = - bz + ln(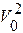 - a) или
- a) или
ln 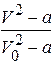 = -bz. (4.15)
= -bz. (4.15)
Из уравнения (4.15) находим
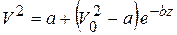 . (4.16)
. (4.16)
Подставляя в (4.16) длину участка z = 2 м и значения a и b из (4.12), получим скорость груза в точке В:  = 65,77 + (172 – 65,77) e-0,8 = 166,074 и, следовательно, VB = 12,88 м/с.
= 65,77 + (172 – 65,77) e-0,8 = 166,074 и, следовательно, VB = 12,88 м/с.
2. Рассмотрим движение груза на участке трубы ВС. На криволинейном участке траектории на точку D действуют сила тяжести 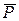 и реакция стенки трубы
и реакция стенки трубы 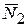 (рис. 4.3). Применим естественные оси плоской траектории точки
(рис. 4.3). Применим естественные оси плоской траектории точки 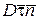 , направив единичный вектор касательной
, направив единичный вектор касательной 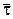 в сторону движения точки. За начало отсчета дуги s примем точку В с начальной скоростью
в сторону движения точки. За начало отсчета дуги s примем точку В с начальной скоростью 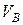 . Основное уравнение динамики точки D на этом участке имеет вид
. Основное уравнение динамики точки D на этом участке имеет вид

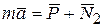 . (4.17)
. (4.17)
Составим первое уравнение системы дифференциальных уравнений (4.3), спроектировав уравнение (4.17) на касательную 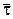 и учитывая, что реакция
и учитывая, что реакция 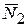 направлена вдоль главной нормали траектории, т. е. по радиусу дуги окружности с центром в точке О:
направлена вдоль главной нормали траектории, т. е. по радиусу дуги окружности с центром в точке О:
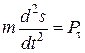 , или, учитывая, что
, или, учитывая, что 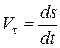 ,
,
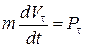 . (4.18)
. (4.18)
Положение точки на дуге окружности будем определять переменным углом φ, откладывая его от радиуса ОВ. В уравнении (4.18) перейдем к новой переменной φ, учитывая, что 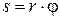 . Тогда
. Тогда
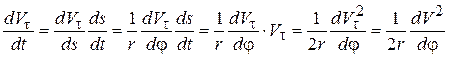 .
.
Сила тяжести 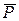 составляет с касательной
составляет с касательной 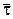 угол 90–γ (рис. 4.3). Из треугольника
угол 90–γ (рис. 4.3). Из треугольника 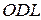 угол
угол 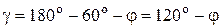 . Следовательно, сила тяжести
. Следовательно, сила тяжести 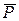 составляет с касательной угол
составляет с касательной угол 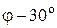 и проекция силы тяжести на касательную равна
и проекция силы тяжести на касательную равна 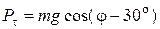 .
.
Тогда уравнение (4.18) примет вид
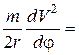
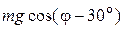 ,
,
Сокращая на массу m и разделяя переменные получим
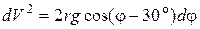 .
.
Взяв от обеих частей интегралы, имеем
 . (4.19)
. (4.19)
 Учитывая, что при
Учитывая, что при 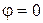 начальная скорость точки равна
начальная скорость точки равна 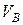 , определим в (4.19) константу интегрирования С:
, определим в (4.19) константу интегрирования С:
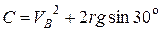 .
.
Следовательно,
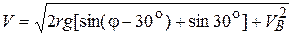 . (4.20)
. (4.20)
Подставляя в (4.20) значение угла  , определим скорость точки в положении С:
, определим скорость точки в положении С:
 12,98 м/с. (4.21)
12,98 м/с. (4.21)
Сравнивая скорости 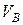 и
и 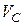 , видим, что потеря скорости на участке сопряжения невелика при относительно малом радиусе скругления r = 0,1 м. С увеличением радиуса r, как видно из формулы (4.21), скорость точки в положении С будет увеличиваться.
, видим, что потеря скорости на участке сопряжения невелика при относительно малом радиусе скругления r = 0,1 м. С увеличением радиуса r, как видно из формулы (4.21), скорость точки в положении С будет увеличиваться.
3. Рассмотрим движение груза на участке ЕС. Начало оси x совместим с точкой С (рис. 4.4). Скорость точки 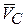 будет начальной для этого участка трубы. Положение точки D будет определяться координатой x. На точку D действуют силы: сила тяжести
будет начальной для этого участка трубы. Положение точки D будет определяться координатой x. На точку D действуют силы: сила тяжести  , переменная сила
, переменная сила 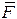 , проекция которой на ось x равна: Fx = - 10sin 3t. Следовательно, при положительном значении функции синуса сила
, проекция которой на ось x равна: Fx = - 10sin 3t. Следовательно, при положительном значении функции синуса сила 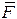 направлена в сторону, противоположную положительному направлению оси x. На точку D действует также нормальная реакция связи
направлена в сторону, противоположную положительному направлению оси x. На точку D действует также нормальная реакция связи 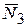 .
.
 Основное уравнение динамики точки D на этом участке будет иметь вид
Основное уравнение динамики точки D на этом участке будет иметь вид
 +
+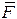 +
+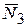 . (4.22)
. (4.22)
Проектируя (4.22) на ось x и учитывая, что 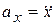 , получим дифференциальное уравнение движения точки
, получим дифференциальное уравнение движения точки
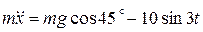
или, разделив обе части уравнения на m = 1,5 кг, при g = 9,8 м/с2 получим
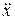 = 6,92 – 6,67sin3t. (4.23)
= 6,92 – 6,67sin3t. (4.23)
Зададим начальные условия:
при t = 0 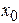 = 0,
= 0, 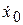 = VС . (4.24)
= VС . (4.24)
Учитывая, что 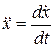 , и разделяя переменные в уравнении (4.23), имеем
, и разделяя переменные в уравнении (4.23), имеем
d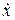 = (6,92 – 6,67sin3t)dt.
= (6,92 – 6,67sin3t)dt.
После интегрирования находим
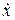 = 6,92t + 2,22 cos 3t + C1. (4.25)
= 6,92t + 2,22 cos 3t + C1. (4.25)
Разделяя еще раз переменные и интегрируя уравнение (4.25), получим
x = 3,46t2 + 0,74sin3t + C1t + C2. (4.26)
Для определения констант интегрирования C1 и C2 подставим начальные условия (4.24) в уравнения (4.25) и (4.26): VС = 2,22 + C1, 0 = =C2, откуда C1 = VС - 2,22 = 12,98 - 2,22 = 10,76.
Следовательно, искомый закон движения груза D имеет вид
x = 3,46t2 + 0,74sin 3t + 10,76t.
Пример 4.2. Рассмотрим предыдущий пример в случае, когда сила сопротивления на участке АВ изменяется по закону 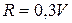 и задано время движения груза
и задано время движения груза 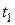 = 2 с на этом участке.
= 2 с на этом участке.
Решение. В этом случае дифференциальное уравнение движения точки D на участке АВ (4.8) будет иметь вид
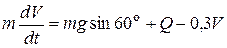 . (4.27)
. (4.27)
Подставим заданные в примере 4.1 величины в уравнение (4.27) и разделим на массу:
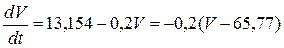 . (4.28)
. (4.28)
Разделяя переменные, уравнение (4.28) запишем в виде
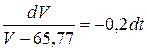 . (4.29)
. (4.29)
Взяв в (4.29) от обеих частей интегралы, имеем:
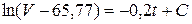 .
.
Константу интегрирования С определим, учитывая начальные условия (4.9):
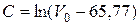 .
.
Следовательно,
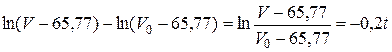 .
.
Откуда при  =17 м/с
=17 м/с
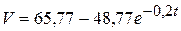 .
.
Значение скорости точки через  = 2 с равно
= 2 с равно
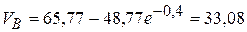 м/с.
м/с.
В силу того, что на участке ВС изменится только начальная скорость 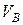 , скорость точки в положении С по формуле (4.21) будет равна:
, скорость точки в положении С по формуле (4.21) будет равна:
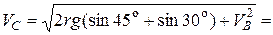 33,12 м/с.
33,12 м/с.
Изменится также константа интегрирования 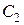 в формуле (4.26):
в формуле (4.26):
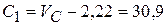 .
.
И следовательно, закон движения груза D на участке СЕ будет иметь вид
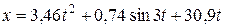 .
.
– Конец работы –
Эта тема принадлежит разделу:
Теоретическая механика. Часть 1
РОССИЙСКОЙ ФЕДЕРАЦИИ... ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ... Государственное образовательное учреждение высшего профессионального образования...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Указания к выполнению контрольной задачи Д1
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов