рефераты конспекты курсовые дипломные лекции шпоры

Раздел Механика
/
Основные задачи динамики материальной точки

Реферат Курсовая Конспект

Выберите учебное заведение

Основные задачи динамики материальной точки

Основные задачи динамики материальной точки - раздел Механика, Теоретическая механика. Часть 1 В Проекциях На Оси Декартовой Системы Координат Векторное Рав...

В проекциях на оси декартовой системы координат векторное равенство (4.1) в общем случае криволинейного движения точки в пространстве запишется в виде

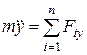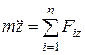, , , (4.2)

где 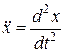, , 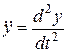– проекции ускорения точки 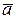; 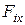, , 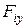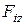–проекции силы 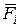на соответствующие оси координат, которые могут быть функциями времени t положения точки x, y, z и проекцией 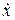, , 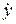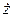скорости .

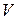Уравнения (4.2) образуют систему дифференциальных уравнений движения материальной точки в координатной форме. При заданной траектории точки ее дифференциальные уравнения движения в проекциях на естественные оси криволинейной траектории записываются в виде

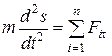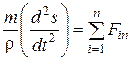, , , (4.3)

где s – дуговая координата, определяющая положение точки на траектории; ρ – радиус кривизны траектории в данной точке; 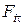, , 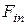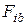– проекции силы 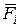на естественные оси траектории: касательную 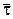, нормаль 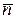, бинормаль .

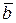На практике выделяют две основные задачи динамики свободной материальной точки, решаемые с помощью уравнений (4.2) или (4.3):

Первая задача (прямая) – считая заданным движение материальной точки массой m, определить равнодействующую сил, вызывающих это движение.

Вторая задача (обратная) – определить движение, которое будет совершать точка массы m под действием заданных сил.

При решении прямой задачи, например с помощью уравнений (4.2), нужно дважды продифференцировать заданные уравнения движения точки, подставить полученные проекции ускорения точки в уравнения (4.2) и определить равнодействующую сил, действующих на точку.

Для решения обратной задачи необходимо найти решение дифференциальных уравнений (4.2). Аналитически обратная задача решается только в частных случаях. Если аналитическое решение невозможно, задача решается численно.

Если систему уравнений (4.2) удастся один раз проинтегрировать, то полученные новые зависимости будут включать время, координаты, их первые производные и три константы интегрирования С₁, С₂, С₃:

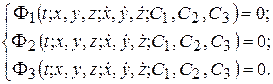(4.4)

Систему (4.4) называют системой первых интегралов уравнений динамики точки.

Если систему (4.4) удастся проинтегрировать еще раз, то полученное решение будет зависеть еще от 3 констант интегрирования С₄, С₅, С₆:

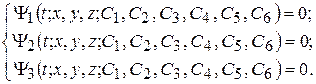(4.5)

Для определения констант интегрирования используют начальные условия, которые задают начальное положение точки 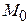(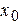, , 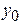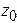) и ее начальную скорость 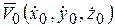в момент времени t = t₀:

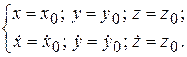(4.6)

Подставляя начальные условия (4.6) в выражения (4.4) и (4.5), составляют шесть уравнений для определения констант интегрирования:

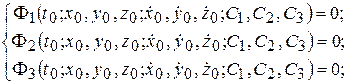
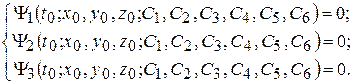
После определения констант интегрирования решение задачи, соответствующее заданным начальным условиям (4.6), записывается в виде

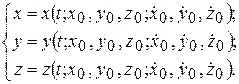
В случае несвободного движения материальной точки уравнения (4.2) и (4.3) будут содержать также неизвестные проекции реакций связей и число неизвестных в общем случае будет превышать число уравнений, Для того чтобы обратная задача была разрешимой, необходимы дополнительные сведения о характере наложенных на материальную точку связей.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Теоретическая механика. Часть 1

РОССИЙСКОЙ ФЕДЕРАЦИИ... ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ... Государственное образовательное учреждение высшего профессионального образования...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Основные задачи динамики материальной точки

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Для студентов заочной формы обучения всех специальностей
Казань 2009 УДК 531.3 ББК 22.21 Х16 Рецензенты:

Основные задачи и аксиомы статики
Статика изучает две основные задачи: 1) Приведение заданной произвольной системы сил к простейшему виду. 2) Вывод условий равновесия твердых тел, находящихся п

При взаимодействии двух тел силы действия и противодействия, возникающие при этом, являются противоравными.
Аксиомы А1-А5 справедливы только для свободных тел, т.е. таких тел, на перемещения которых не наложено никаких ограничений. Несвободным телом н

Моменты сил. Главный вектор и главный момент системы сил
Для решения основной задачи статики – определение условий равновесия твердых тел, находящихся под действием системы сил, необходимо ввести понятия моментов силы. Момент силы

Основная теорема статики. Уравнения равновесия
Основная теорема статики: Для уравновешенности системы сил необходимо и достаточно чтобы ее главный вектор и главный момент относительно произвольной точки О равня

Частные случаи
1)

Система сходящихся сил
В этом случае линии действия всех сил, приложенных к твердому телу, пересекаются в одной точке. Выбирая начало координат в этой точке, получим три условия равновесия для сходящейся системы сил:

Система параллельных сил
Направив одну из осей, например z, параллельно силам, получим три скалярных условия равновесия: ,

Указания к выполнению контрольной задачи С1
Задача С1 - на равновесие тела под действием плоской системы сил. В вариантах ([1], табл. 1.1, рис. 0, 1, 3, 5, 6, 8, 9) жесткая рама опирается у конца A на неподвижный шарнир (см. пример 1.

Указания к выполнению контрольной задачи К1
Задача К1- на определение кинематических характеристик точки по заданным в координатной форме уравнениям движения. Варианты задач различаются траекториями, которыми являются окружно

Указания к выполнению контрольной задачи К2
Задача К2 – на определение угловых скоростей звеньев и скоростей отдельных точек плоского многозвенного механизма, состоящего из 4 стержней и ползуна В, соединенных друг с другом и неподвижн

Инерциальные системы отсчета. Аксиомы динамики
Материальной точкой в механике называют простейшую модель физического тела любой формы, размерами которого и вращением можно пренебречь в рассматриваемой задаче и которое можно прин

Изолированная материальная точка либо покоится, либо движется равномерно и прямолинейно до тех пор, пока на нее не подействуют силы.
Под изолированной материальной точкой понимается материальная точка, свободная от силового воздействия. Система отсчета, в которой справедлива аксиома А1, называется инерциальной системой отсчета.

Указания к выполнению контрольной задачи Д1
Задача Д1 относится ко второй основной задаче динамики материальной точки. В вариантах задач ([1],Табл. 4.2, усл. 0, 2, 4, 6, 8) сила сопротивления среды, действующая на груз, завис

Краткие теоретические сведения
Рекомендуемая учебная литература: [2], гл. XXV, § 121–127, c. 301–323; [4], гл. X, § 10.1–10.5, c. 204–222. Механическая система. Центр масс Под ме

Моменты инерции
Инерционные свойства механической системы определяются шестью моментами инерции: ;

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Теоретическая механика. Ч. 1. Программа, методические указания и контрольные задания. Для студентов-заочников всех специальностей. Л.Ш. Хакимуллина, Ю.Я. Петрушенко. - Казань: КГ

Маркин Юрий Сергеевич
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. ЧАСТЬ 1 Учебно-методическое пособие к выполнению контрольных заданий (с примерами решений) для студентов за