Указания к выполнению контрольной задачи С1

Задача С1 - на равновесие тела под действием плоской системы сил. В вариантах ([1], табл. 1.1, рис. 0, 1, 3, 5, 6, 8, 9) жесткая рама опирается у конца A на неподвижный шарнир (см. пример 1.1), а у конца В либо на подвижный шарнир, либо на стержень. В вариантах ([1], табл 1.1, рис. 2, 4, 7) жесткая рама у конца D заделана в стену (см. пример 1.2). Задачи на равновесие твердых тел следует решать в следующей последовательности:

1. Выделить тело, равновесие которого необходимо рассмотреть в данной задаче. Изобразить его на чертеже.

2. Приложить к телу активные силы. Если есть распределенная нагрузка, заменить ее равнодействующей, определив ее модуль, направление и точку приложения.

3. Выяснить, какие связи наложены на выделенное тело. По принципу освобождаемости от связей А6 отбросить связи и на их место приложить к телу соответствующие реакции связей.

4. Выбрать оси координат и для полученной системы сил (активных сил и реакций связей) составить уравнения равновесия.

5. Из полученной системы алгебраических уравнений определить неизвестные реакции связей.

 

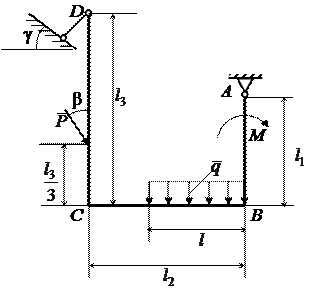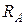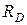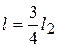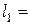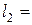Пример 1.1. Жесткая рама АВСD (рис. 1.18), расположенная в вертикальной плоскости, опирается у конца А на неподвижный шарнир (рис. 1.8), а у конца D на стержень (рис. 1.10). Определить опорные реакции и , возникающие при действии силы Р = 8 кН, пары сил с моментом М = 30 кН·м, равномерно распределенной нагрузки с интен-сивностью q = 2 кН/м вдоль отрезка . Даны размеры рамы и углы: 2 м, 2 м, 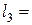3 м, γ = 45°, β= 30°.

 

 

Рис. 1.18

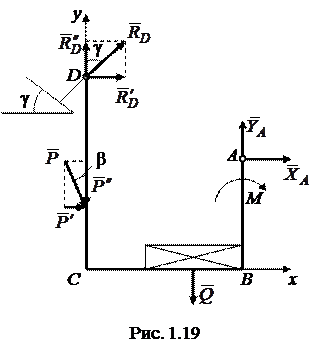Решение. Выделяем раму АВСD (рис. 1.19). Заменим распреде-ленную нагрузку равнодействующей Q, численно равной произведению интенсивности q на длину действия нагрузки:

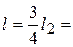1,5 м, 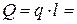3 кН.

Сила Q будет приложена посередине длины и сонаправлена вектору 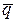(рис. 1.19). Приложим к раме силу 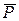и пару сил с моментом М. Применяя аксиому освобож-даемости от связей А6, действие стержневой опоры у конца D заменим реакцией 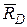, направленной вдоль стержня (рис. 1.10, 1.19). Действие цилиндрической шарнирно-неподвижной опоры у конца А рамы заменим реакцией 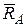. Выберем систему координат Сху и разложим по аксиоме параллелограмма сил А3 реакцию 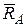, направление которой заранее неизвестно, на составляющие 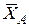и 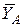параллельно осям х и у (рис. 1.19). Составим уравнения равновесия для полученной произвольной плоской системы сил в первой форме (1.8):

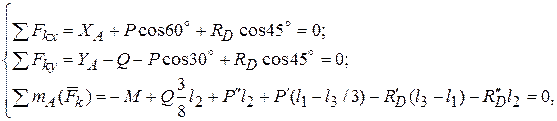(1.12)

 

где , , .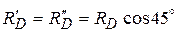

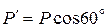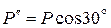В первых двух уравнениях системы (1.12) проекции сил 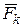, например, на ось х равны

,

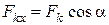где угол α откладывается от оси х против хода часовой стрелки (рис. 1.20), причем, если угол α острый, то проекция силы берется с положительным знаком, если тупой – с отрицательным знаком.

 

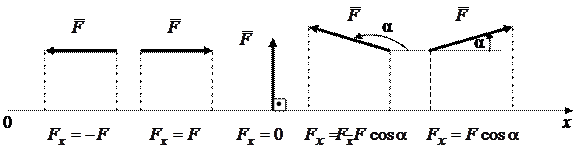Рис. 1.20

 

В уравнении моментов (третье уравнение системы (1.12)) за точку, относительно которой по формуле (1.7) составляли моменты сил, приняли точку А. При вычислении моментов сил 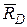и 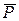воспользовались теоремой Вариньона, предварительно разложив силы по аксиоме А3 на составляющие (рис. 1.19):

, .

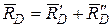Так как точка А находится на пересечении линий действия сил 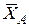и 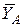, их моменты равны нулю. Поэтому за счет выбора точки А в третьем уравнении имеем только одну неизвестную реакцию :

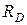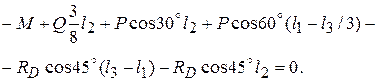
Откуда

– 4,66 кН.

Подставляя значение реакции 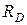в первые два уравнения системы (1.12), определим составляющие реакции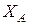и :

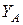–0,7 кН, 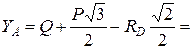13,22 кН.

Знак минус в ответе означает, что реакция 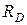и составляющая 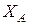имеют направление, противоположное указанному на чертеже (рис. 1.19).

 

Пример 1.2. Рама АВСD у конца D заделана в стену (рис. 1.21). Определить реакции заделки при заданных в примере 1.1 размерах рамы и величинах нагрузки.

Решение. На выделенную раму АВСD (рис. 1.22) дейст-вуют сила Р = 8 кН, пара сил с моментом М = 30 кН·м. Равно-действующая распределенной нагрузки равна

 

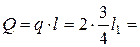3 кН.

Применяя принцип освобо-ждаемости от связей А6, действие жесткой заделки у конца D заменим составляющими реакции заделк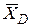и и 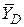и парой с реактивным моментом 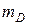(рис. 1.11, 1.22). Выберем систему координат Сху и составим уравнения равновесия для произвольной плоской системы сил в форме (1.8), составляя уравнения моментов относительно точки D:

 

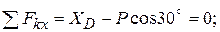
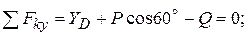(1.13)

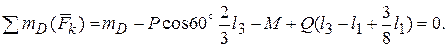
Из полученных алгебраических уравнений (1.13) определяем неизвестные величины:

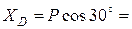6,93 кН;

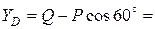–1 кН;

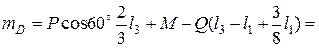32,75 кН·м.

 

 

 

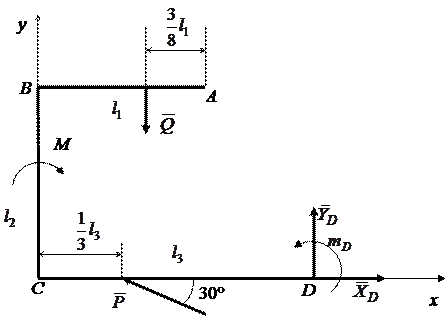
Рис. 1.22