ПРЕДСТАВЛЕНИЕ МОДЕЛИ, ИСПОЛЬЗУЮЩЕЕ СЛУЧАЙНЫЕ ИМПУЛЬСЫ
ПРЕДСТАВЛЕНИЕ МОДЕЛИ,
ИСПОЛЬЗУЮЩЕЕ СЛУЧАЙНЫЕ ИМПУЛЬСЫ
Мы видим, что линейная модель может быть представлена как выход линейного фильтра.
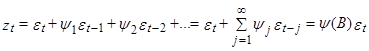(9)
входом которого является белый шум.
Иногда полезно представить модель АРПСС в форме (8). Покажем, что веса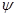 
процесса АРПСС можно получить прямо из представления модели в виде разностного уравнения.
Если применить к обеим сторонам (9) обобщенный оператор авторегрессии f(B), получим: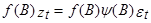 
. Однако, т.к. 
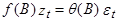, отсюда следует, что
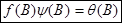(10)
Следовательно, веса 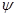можно получить, приравнивая коэффициенты при одинаковых степенях В в уравнении
(11)
Заметим, что для j, больших, чем p+d-1 и q, т.е. для таких, что
j>p+d-1, если p+d-1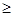
q,
j>q, если p+d-1<q,
веса 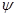удовлетворяют разностному уравнению, определенному обобщенным оператором авторегрессии, т.е. 
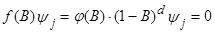(12)
где В действует на индекс j. Тогда для достаточно больших j веса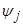 
представлены совокупностью полиномов, затухающих экспонент и затухающих синусоид от аргумента j.
Пример,
Рассмотрим АРПСС (1,1,1), для которого
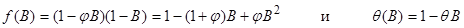
Подстановка в (11) приводит к:
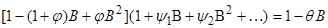
отсюда:
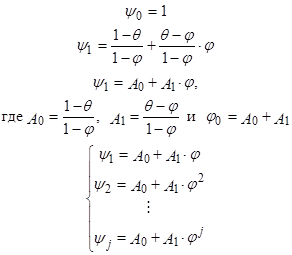
Отсюда мы можем представить модель (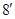
) эквивалентным выражением:
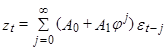(13)
Т.к. 
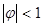, веса 
при больших j приближаются к 
, так что импульсы 
, которые внесли свой вклад в отдаленном прошлом, получают постоянный вес .
ИНДЕНТИФИКАЦИЯ МОДЕЛЕЙ
Конкретная цель состоит в том, чтобы , во-первых, получить некоторое указание на то, какие значения p, d и q нужны в общей линейной модели АРПСС, и, во-вторых, выбрать некоторые начальные значения параметров. Полученная таким способом пробная модель является отправной точкой для применения более формальных и эффективных (способов) методов оценивания.
Наша задача – идентифицировать подходящий подкласс моделей их общего семейства моделей АРПСС 
которые может быть использован для описания данного временного ряда (иногда целесообразно рассматривать слегка обобщенную форму модели АРПСС, полученную добавлением постоянного члена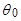 
).
Наш подход состоит в следующем:
a) Мы будем брать конечную разность от 
столько раз, сколько необходимо, чтобы обеспечить стационарность, в надежде свести изучаемый процесс к смешанному процессу авторегрессии – скользящего среднего 
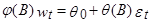, где 
.
b) Идентифицировать результирующий процесс АРПСС.
Наш основной инструмент для реализации a) и b) автокорреляционная и частная автокорреляционная функции.
МЕТОДИКА ИДЕНТИФИКАЦИИ
Ранее было показано, что автокорреляционная функция стационарного смешанного… (8)ИДЕНТИФИКАЦИЯ РЕЗУЛЬТИРУЮЩЕГО
СТАЦИОНАРНОГО ПРОЦЕССА АРСС
Приняв предварительное решение о величине d, мы далее изучаем общий вид выборочной автокорреляционной и частной автокорреляционной функции… При этом мы должны помнить характерные особенности поведения теоретической… В то время как автокорреляционная функцияНАЧАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ
I. НАЧАЛЬНЫЕ ОЦЕНКИ ДЛЯ ПРОЦЕССОВ СКОЛЬЗЯЩЕГО СРЕДНЕГО
(9) Выражение (9) для через дает q уравнений с q неизвестными. Предварительные…II. НАЧАЛЬНЫЕ ОЦЕНКИ ДЛЯ ПРОЦЕССОВ АВТОРЕГРЕССИИ
В частности, для процесса АР(1): И для АР(2): (10) Соответствующая формула, вытекающая из уравнений Юла-Уокера, для процессов высшего порядка может быть получена заменой…III. НАЧАЛЬНЫЕ ОЦЕНКИ ДЛЯ СМЕШАННЫХ ПРОЦЕССОВ АВТОРЕГРЕСИИ – СКОЛЬЗЯЩЕГО СРЕДНЕГО
В дальнейшем часто будет обнаруживаться, что-либо после взятия нужного числа разностей ряд будет наиболее экономично описываться смешанным процессом… Указанием на смешанный процесс является тот факт, что автокорреляционная функция затухает. Другой факт, помогающий…ОЦЕНИВАНИЕ МОДЕЛИ
После того, как процесс идентификации привел к пробному варианту модели, нам необходимо получить эффективные оценки параметров. После этого подогнанная модель будет подвергнута диагностической проверке и тестам на качество подгонки.
МОДЕЛЬ БОКСА-ДЖЕНКИНСА
Одной из основных проблем применения такой модели является определение эффективных оценок ее параметров. Здесь имеется 3 типа параметров: порядок разности d, авторегрессионые… В общих чертах процедура выглядит следующим образом:ОЦЕНИВАНИЕ ПАРАМЕТРОВ
ПРОЦЕССА СКОЛЬЗЯЩЕГО СРЕДНЕГО
Бокс, Дженкинс “Анализ временных рядов”) I. Начальные оценки параметров процессов СС(q):СПЕКТРАЛЬНЫЙ АНАЛИЗ
(и гармонический)
(Выявление скрытых периодичностей
с помощью гармонического и спектрального анализа)
(Т.Андерсен “Стохастический анализ временных рядов”)
ОРТОГОНАЛЬНЫЕ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Тригонометрические функции являются периодическими с периодом , т.е. (1) Отсюда следует, чтоПРЕДСТАВЛЕНИЕ ФУНКЦИИ В ВИДЕ РЯДА ФУРЬЕ
Итак, функции , определенные на множестве , образуют ортогональный базис, и всякую функцию, в том числе и временной ряд , определенный на отрезке ,… (15) где и при четном Т (т.к. ). Действительно,ТЕОРЕМА ПАРСЕВАЛЯ
для четных Т (21) Действительно, если , то . Возведя (15) в квадрат и просуммировав i, j по t…СПЕКТРАЛЬНЫЙ АНАЛИЗ
График зависимости от периода называется периодограммой. Применение ортогональных функций, рассмотренных выше, определяет периодограмму в точках . … График зависимости от частоты (график спектра) удобнее, т.к. квадраты… График спектра нужен для более наглядного изображения распределения дисперсии между отдельными частотами. Если частоте…СВЯЗЬ ВЫБОРОЧНОГО СПЕКТРА С